Solid State Plasma Models
Have you noticed that in most if not in all the textbooks on atomic physics, statistical mechanics -
there is no clear description:
- What is the subject of statistical averaging?
- How you do the statistical averaging ?
Do you count them (particles) one, two, three ... etc. ?
But they are moving all the time.
Do you count them as at the given point ?
But what is the point ?If in the some physical theories (string theory, for example) the point could be taken as a one which is much less than the volume of 10(-105) m^3 =10(-78)nm^3 ??
There are theories recognizing the even smaller spatial scales.
Having said this, we are in no way saying some words of opinion or support in favor of this strangled theory, see more on that in -
" The Trouble With Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next"
From that piece - "The social constructivists
claimed that the scientific community is no more rational or
objective than any other community of human beings. ........
We tell our students that belief in a
scientific theory must always be based on an objective evaluation of
the evidence. Our opponents in the debate argued that
our claims about how science works were mainly propaganda designed to
intimidate people into giving us power, and that the whole
scientific enterprise was driven by the same political and
sociological forces that drove people in other fields."
Following our agenda, meanwhile, in the one scale mathematics the Point is the point (dot) - No Dimension in any direction!
At least - as for now on.
So, what to do with this? When the any almost (and might be everyone), and definitely all those we are talking
about here particles are larger then the point? If we acknowledge the existence of different scales
and treat physics on each scale REALLY - we need to address this issue seriously.
Do these particles come and leave the point if particle itself much larger then the point and we need to consider the centers of particles and their closest distance to the point?
So, we need to consider also the brim of the particle touching the Point, right ?
Well, please, don't remind me on the Quantum Mechanics some postulates, there should not be the sacred cows in physics, is this correct? We touch these subjects later on in this section.
Then we need to recognize that we are talking about the VOLUME for particle statistics, volume around of our point.
Even if we do not want to say this?
Well, this is not the physical rave, workers just don't see these "small" inconsistencies with definitions as a problem as long as they continue to do their way of living?
Now, let we drop the point definition off consideration for a while.
And so, let's do the volume to count for the statistics of the particle's behavior?
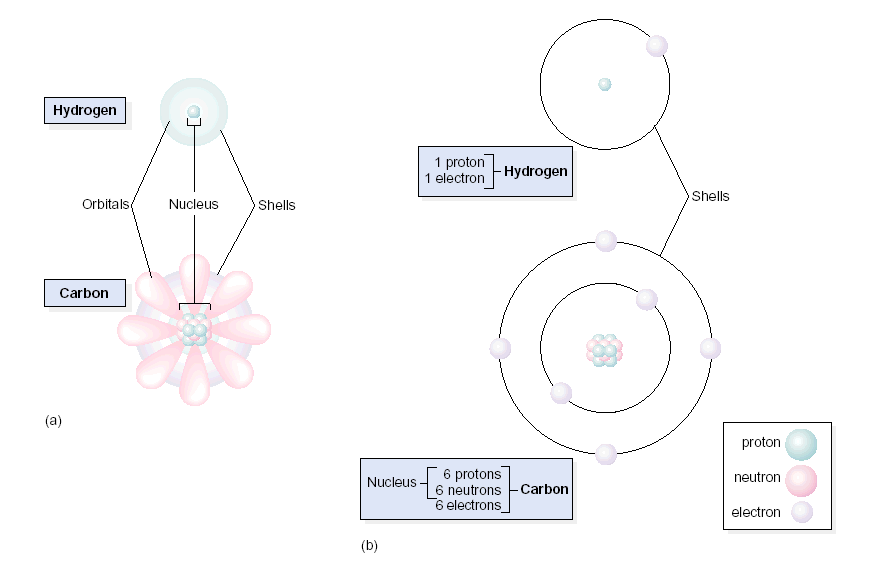
What is the volume to take for statistics? In most, if not in any book on solid state and related
software doing the MD modeling, statistics, they like to show
the cube with the atoms, molecular movements -
And these objects are moving all the time - leaving and coming back into that selected volume -
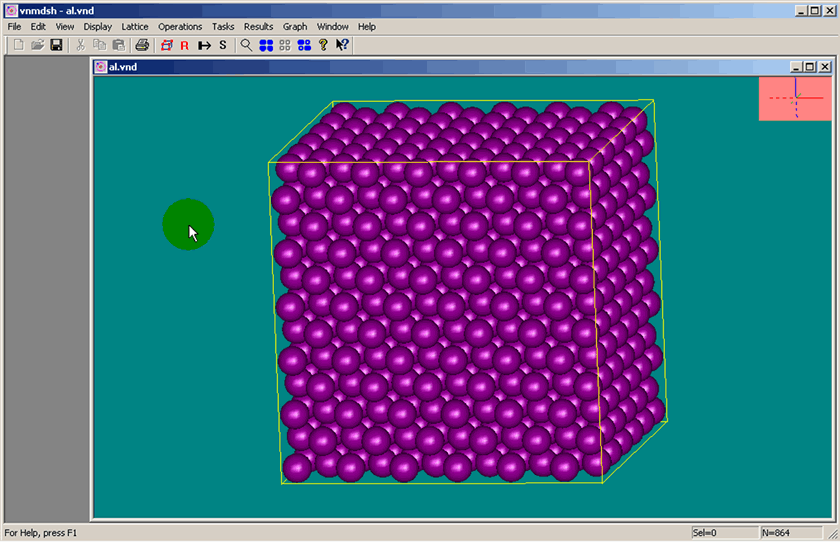
![]()
What does this mean if taking these movements to the mathematics strictly as in Hierarchical Scaled Physics (HSP)?
Well, we come to the Volume-Surface relations in mathematics and physics, right?
Then, we need to go first through the introductory parts in all this new for most people in atomic physics approach to the mathematics of the Point (Dot) at the different spatial scale deliberation -
Now we understand - this is not such a simple issue to build the conservative governing equations in this physics field - as the Plasma Physics.
Each and every time when there are needs to talk, construct, erect the mathematical model for some specific plasma physical model - we need to find out
- What is the single object (particle, anything) that we are dealing with ?
and
- What is the Averaged subject we want to declare as directly related, tight to our single object when even it is not might be found at the definite point (point ?) in the given space at the sought time ?
Many things discussed now in the plasma physics are already many times being concerned, debated and presented in the multiphase fluid mechanics, see our review on multiphase modeling in fluid mechanics in -
Including the modeling, averaged governing equations derivation.
Still, it is a big difference in physics and this should be mirrored in the mathematical modeling in plasma physics.
We are presenting here just few selected points and mathematical outcomes for some modeling needs in solid state plasma (in other sub-sections, might be found various related issues).
Again, we won't be involved into great number of plasma physics concerns, but few selected major points of mathematical modeling for multiphase collective subjects in plasmas are of interest for us as for the same reason - those are the multiphase, two- and more scale physical fields and their mathematics is the mathematics of HSP-VAT.
We believe this will grow in time as this already happened with
multiscale, heterogeneous, hierarchical media in other physical sciences through the last 40+ years.
Any arguments, if not stupid would be considered openly here.
When one starts to build the mathematical model for a solid state plasma physics problem, one of the main issues is - What is the Field's meaning? What does it mean - Local and Non-local, or Averaged, of the Upper (another) Scale value for this Field?
Solid State and Complex Plasmas Multiscale Governing Equations
Introduction
A solid state is a medium which fairly can be recognized as a heterogeneous medium at any chosen scale when we judge the phenomena in each of two- (or more) "phases" and looking for these phenomena to be modeled with proper mathematical concepts.
The great number of facts evidence in a favor of interplay of different physical processes in each "phase" (consistent component of the physical picture) at the same scale while they are being the important elements of a common process or transport.
There is the need to understand the physics and to model multiscale characteristics in heterogeneous media. Also, at present, the common majority of experimental methods are designed for homogeneous processes or like homogeneous, making it difficult to assess the impact of various features of heterogeneity.
The governing hydrodynamics, electrodynamics, and energy transport equations used in most past work in plasma physics had treated particulate transport and wave propagation, whether they are of differential or integro-differential type, as if they were in a homogeneous medium.
This type of idealization significantly reduces the robustness of the physical description loosing the relationship between each scale from atomic to microscale parameters on the macroscopic behavior.
The present work continues our suggested first in 90th the mathematical language for scaled formulation of heterogeneous problems in electrodynamics and plasma physics - the tools of heterogeneous media scaled description - Heterogeneous Scaled Physics-Volume Averaged Theory (HSP-VAT):
and Optics (including scattering issues)
and Acoustics
At the present time it is the only consistent and reliable theory available for multiscale either 1D or 3D, linear or nonlinear, cross-connected between scales mathematical statement tasks. The VAT approach has been successfully applied in the last twenty plus years to a large number of difficult scaled problems in fluid mechanics, thermal physics, meteorology, electrodynamics, acoustics and other disciplines and technologies for heterogeneous media treatment.
Some Basic Postulates Used in the Conventional One Scale Plasma Physics
Here we intentionally will try to give references to the old publications, that are in a direct connection to the main theories of sub-atomic world and in current time COHP books, manuscripts, textbooks, articles, etc.
In the book by Steel and Vural (1969) we can find -
We can read in the page 43:
"In summary, the basic equations of electron plasma considered as a conducting fluid are
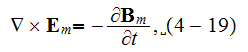
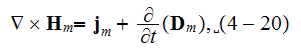
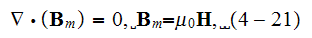
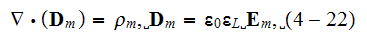
where the equation of "averaged" velocity

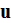 conservation is
conservation is
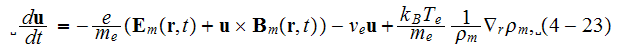
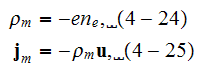
where

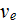 is the effective collision frequency coefficient.
is the effective collision frequency coefficient.
The current density

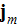 and the charge density
and the charge density

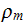 obey the equation of continuity
obey the equation of continuity

which follows from Eqs. (4-20) and (4-22). In equation (4-23) we assumed that the pressure is isotropic. "
"We now must relate the source terms to the dynamical motion of the electrons:
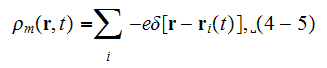
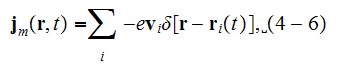
where
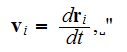
This text above, the equations ground and the definitions for the charge density

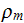 and the current density
and the current density

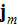 are clearly speak on the volumetric description of the physical fields
(functions).
are clearly speak on the volumetric description of the physical fields
(functions).
We see - that in this excerpt in the conventional one
scale homogeneous physics the subject of the point in the Dirac's function and
of the electron's location point is taken as the same by the definition. That
means - that either the electron is of no dimensions and the size or the
delta function

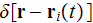 acts over the volumetric space occupied by the electron.
Which is not a volumeless.
acts over the volumetric space occupied by the electron.
Which is not a volumeless.
Both assumptions are contradict mathematically.
Still, more of the physical ground is that - the delta function has spread it's qualities over the volume occupied by electron. O.K., but this is the volumetrical integration even for a single electron! And should be of volumetrical nature for the cloud of electrons in the solid state volume taken as the characteristical one.
In both situations for the one scale homogeneous physics of the first half of the 20-th century it was convenient to have not (or to ignore) the description of the volume for integration.
It has no clear description - just the "Volume" and this sum
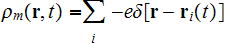 ! When everybody
knows that to perform an integration one needs to depict exactly - What is the space for integration ? Any feature of it is needed for integration.
! When everybody
knows that to perform an integration one needs to depict exactly - What is the space for integration ? Any feature of it is needed for integration.
Electrodynamics Basic Governing Equations in One Scale Plasmas
Consider as the already like "averaged" homogeneously conventional Maxwell governing equations in semiconductor plasma
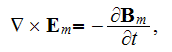
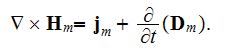
In these above GE the variable's fields are already considered as the "averaged" variables - which is completely wrong, as soon as the fields are acting in Heterogeneous media, but Maxwell equation are used to be developed (at least justified and explained) on the base of Homogeneous GO theorem.
A soon as we regard the scales in solids the ones that can be characterized as
the meso- nano- and atomic scales we have to admit that the variables

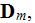

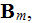

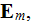

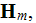 in this set and the equations itself can not be accepted as averaged, unless
we formalize at least the two scale physics and their related mathematical
models more strictly than just saying that these variables are "averaged"
somehow. We would shortly feature below the few moments and arguments of the
HSP-VAT applied to the formulation of basic governing equations in solid state
and complex plasmas theories.
in this set and the equations itself can not be accepted as averaged, unless
we formalize at least the two scale physics and their related mathematical
models more strictly than just saying that these variables are "averaged"
somehow. We would shortly feature below the few moments and arguments of the
HSP-VAT applied to the formulation of basic governing equations in solid state
and complex plasmas theories.
The Representative Point Mathematical Definition and its Physical Meaning for Different (and Neighboring) Scales.
We would like to say some notes regarding the definitions of these concepts, those taken as being granted. When the problem, the physics of the problem demanding and has the features of different scale physics, then we need to do something about it.
The easiest way is just to ignore this and say for a particular problem - that "these are the respected scale features."
As it is done with, for example, the Molecular Dynamics (MD) simulations. After simulation of the huge amount of atoms or molecules in the box, then the whole box properties are declared as the specified material's properties.
The trick is that in MD also used numerous atomic scale physics approximations and assumptions, and still the results can be driven to a reasonable proximity to experiment, or vice versa.
The reason to distinguish the point defined local and the non-local field's values at the same coordinate system is following the same famous theorems we are discussing here in this website - the Ostrogradsky-Gauss (OG) (or Gauss-Ostrogradsky - GO) theorem
or the Heterogeneous Whitaker-Slattery-Anderson-Marle (WSAM) kinds of theorem.
Thus, we start with the definition of a point, a dot used in the mathematical formulation of physical problems (not a strict one, which definition we leave for a more appropriate situation with the mathematics discussed).
Definition 1:At the known and assigned previously system of coordinate the point is the object with no dimension in any of the three spatial (cartesian) coordinates, and this object has the descriptive features, which determine the location of that point in the assigned system of coordinates. The point located physical field's property has this spatial point determined value.
Following the OG theorem we now know that - if at any point with the coordinates inside of the problem's domain is known the functional dependency for a physical field, which in the most of physical sciences right now is the partial differential or just differential equation(s), then we imply that the domain which served for the derivation of this equation via the OG theorem was the domain of the Lower subspace - because in that theorem we start doing an integration over the Homogeneous finite volume and the finite surface(s).
Now - why not apply the same concept to the heterogeneous media, which means - that after the averaging provided according to the one of the WSAM theorems - we get the mathematical equation (dependency) of the higher (another) space. With the corresponding spatial dependencies and the topology of the physical spatial fields.
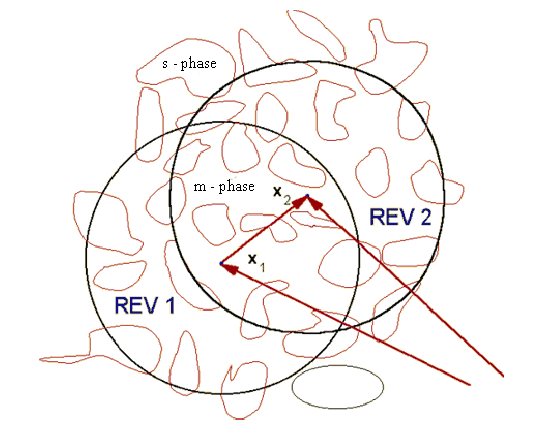
Figure 4: Representative elementary averaging volumes (REVs) with the fixed points of representation.
With the one substantial different feature - we can not infinitely reduce the
size (well, if we not considering the sizes of kind of the string theory when the
physical point could be taken as a one which is much less than the volume of

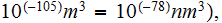 the volume of this domain - because we want to keep the most of descriptive
features of the both (or more) phases inside of our spatial domain(s).
the volume of this domain - because we want to keep the most of descriptive
features of the both (or more) phases inside of our spatial domain(s).
The Upper Space point when connected to the Lower Scale Domain might reflect, determine, and establish the features of communications between the both space physics'. These features can be of different physical description in accordance to their respected space physics definitions. And vise versa - the Higher Space point physics might control, govern, reflect, and determine in some ways the properties of the Lower Scale physical Domain.
-
It is easier to discuss and argue in favor of these definitions right now - after the number of problems were solved in the said mode - when the Lower and Upper scale HSP-VAT governing equations were connected Directly before and during their respected solutions.
The brightest example for viewing the situation as the said above is the transition from the atomic (atomistic) spatial scale dependencies - dependencies described by atomic physics discipline, to the continuum physics laws and dependencies.
Solid State Plasma REV
Meanwhile, no one seems can argue that the media in solid state of most of
origin are heterogeneous media. If we would like to except the notion that the
Dot, the Point on the Lower Scale in these physical fields are related,
assumed as, to the volume approximately with

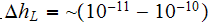

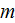 the side of the cube, then we can say that the Representative Elementary
Volume (REV) or Point (Dot) in Plasma Physics fields, for governing equations
for these kinds of fields - the commonly explained and excepted fields are
the side of the cube, then we can say that the Representative Elementary
Volume (REV) or Point (Dot) in Plasma Physics fields, for governing equations
for these kinds of fields - the commonly explained and excepted fields are

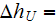

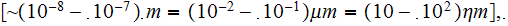 or
or

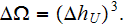
And this is the three orders of linear one dimension magnitude separating the Point in the Lower Scale field and the Point of the Upper Scale physical field. Reasonably enough for most of theoretical schemes.
With meaning of the physical representative (REV) Upper Scale point (REV) variable of the size of

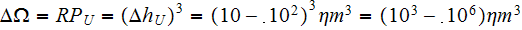 .
.
We do not discuss here in this work the lower than

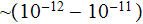

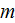 spatial scales of physical fields as well as their corresponding physical
notions, objects (as, for example, the string theory and strings size of
spatial scales of physical fields as well as their corresponding physical
notions, objects (as, for example, the string theory and strings size of

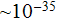

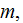 when
a point could be taken as a one which is much less than the volume of
when
a point could be taken as a one which is much less than the volume of

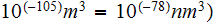 ,
their properties, peculiarities, relation to the atomic scale physics etc.,
etc.
,
their properties, peculiarities, relation to the atomic scale physics etc.,
etc.
But we do this in other studies related.
For fields of dusty plasmas with the

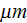 size "dust" particles the REV size would be reasonably taken as -
size "dust" particles the REV size would be reasonably taken as -

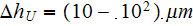 with the Lower scale point of the same size
with the Lower scale point of the same size

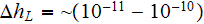

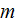
Electrodynamics Basic Governing Equations in Two Scale Solid State Plasmas
The full description of derivation of VAT non-local Upper scale electrodynamics governing equations is given in publications by Travkin et al. (1999, 2001) and some earlier works.
We use the notion that the Point (dot) in our averaged (Upper Scale) governing
equations of electrodynamics in solid state are considered on the scale of

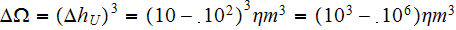 .
.
Here we will write down only few governing equations, as for the electric
field those after averaging over the phase

 using
using

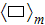 become
become
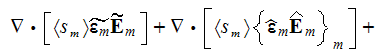
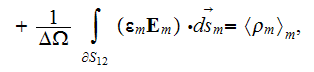
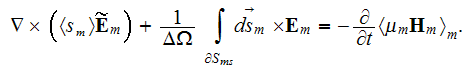
The phase averaged magnetic field equations are
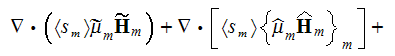
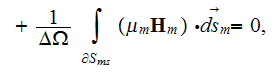
and
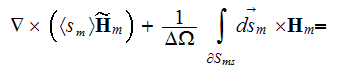
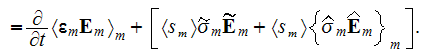
These equations and some of their variations as, for example,
the electric field wave equation
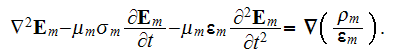
becomes (assuming the fixed (unmovable) interface surfaces)
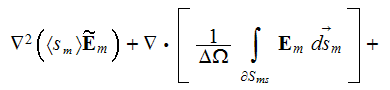
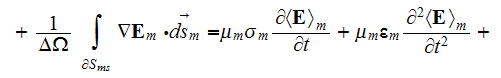
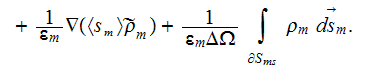
An analogous form has the often used averaged equation for the time-harmonic electric field
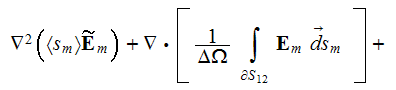
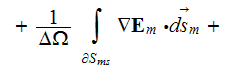
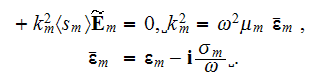
with

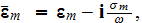
The VAT based transient charge conservation equation in heterogeneous media obtains the form
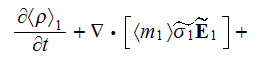
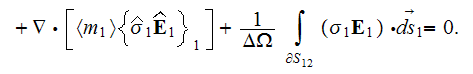
As it can be observed the most advantages feature of the heterogeneous media
electrodynamics equations is the inclusion of terms reflecting phenomena on
the interface surface

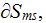 and that fact can be used to incorporate morphologically precisely multiple
effects occuring at the interfaces.
and that fact can be used to incorporate morphologically precisely multiple
effects occuring at the interfaces.
Now we will add here for the completeness of the picture the averaged nonlinear equation for the electric potential
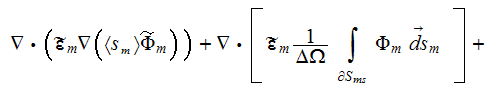
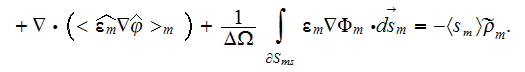
Dusty (Complex) Plasmas - Local and Non-local Presentation. Does Local Magnitudes Meaning That?
We consider here the following scales to make hierarchical scaled physical processes cross-connection of the different scales physics in the dusty plasmas evident. The models for reflecting each scale processes and dynamics are based on the recognition that the point determined and the averaged over the some domain physical fields are the different fields, cross-connected, directly tight but still the different physical fields and require the different mathematical models for each one.
For physical fields of dusty plasmas with the

 size "dust" particles the REV size would be reasonably taken as the Upper
scale 1D span of the size -
size "dust" particles the REV size would be reasonably taken as the Upper
scale 1D span of the size -

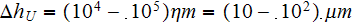 with the Lower scale point of the same size
with the Lower scale point of the same size

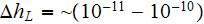

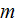

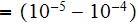

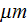
This multiscale physical object does need the fields with meaning of physical
representative (REV) point variable of the size of

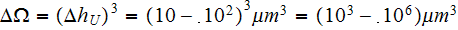

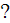
In the plasma chamber of the size

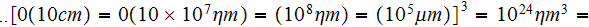

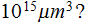
Probably - yes, inspite the huge amount of calculation this size REV domain
needs for.
For some statements this span of scales

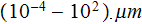 is most likely too large, and depending on the dusty particles size,
distribution features, and physics of that plasma the third intermediate scale
might be introduced as of
is most likely too large, and depending on the dusty particles size,
distribution features, and physics of that plasma the third intermediate scale
might be introduced as of

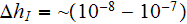

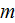

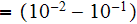

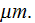
As it is commonly accepted in the one scale plasma physics and usually can be taken as this kind (with, well, not important anyway variations) of governing equations for dusty (complex) plasmas:
as the conservation of electrons equation (assumed as with the averaged number

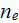 )
)
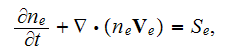
and the equation of electron momentum conservation
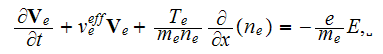
with the effective rate of electron collision

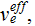
which we may comparing to the electrons momentum conservation equation of Fushinobu et al. (1995)
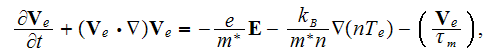
where included the terms - the last term

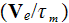 symbolizing the momentum change due to electron collisions with particles in
the medium.
symbolizing the momentum change due to electron collisions with particles in
the medium.
Here one would explain that

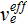 could be taken as
could be taken as

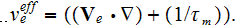
In all other governing equations in this kind of the one scale studies can be seen
the similar particles interaction reflecting the phenomenological terms.
Interesting enough, that all the source terms as, for example,

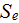 which is the overall rate of production-destruction of electrons are given through the coefficients
which is the overall rate of production-destruction of electrons are given through the coefficients
where

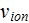 is the rate of electron impact ionization of the neutral particles,
is the rate of electron impact ionization of the neutral particles,

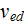 is the rate of collection of plasma species by the dust grains,
is the rate of collection of plasma species by the dust grains,

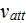 is the rate of electron attachment to the neutral atoms resulting in negative
ion production,
is the rate of electron attachment to the neutral atoms resulting in negative
ion production,

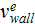 is the particle (electrons) loss at the walls of the discharge" chamber.
is the particle (electrons) loss at the walls of the discharge" chamber.
In other conservation equations the same kind of production-destruction rates
are explained as the nessessary parts of the balance in each process.
So - all these production-destruction, as well as collision rates terms - are
the result of knowledge about real events in the atomic scale plasma, and at
the same time - the helplessness in terms of really strict explanation and
derivation of models for these existing effects.
We need to say that these are not the averaged equations as well.
For example, the conservation of electrons really "phase" averaged variables equation will have the form
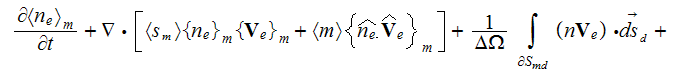
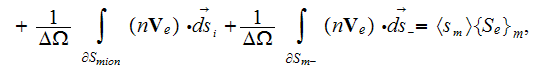
where

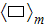 means averaging over the major phase which is the interatomic and
inter-particle subvolume of the REV volume in the dusty plasma,
means averaging over the major phase which is the interatomic and
inter-particle subvolume of the REV volume in the dusty plasma,
where the r.h.s. term might be annihilated because of the multiphase presense in the subvolume and of the correct averaging of the gradient term in the left hand side of this equation,
where

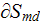 is the "interface" (real or imaginable) of impact with the dust "phase" and
scatterers,
is the "interface" (real or imaginable) of impact with the dust "phase" and
scatterers,

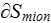 is the "interface" (real or imaginable) of impact with the neutral and ion
"phase", while
is the "interface" (real or imaginable) of impact with the neutral and ion
"phase", while

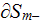 is the "interface" (real or imaginable) of impact with the negative ion
"phase."
is the "interface" (real or imaginable) of impact with the negative ion
"phase."
It will be assumed here that not only immobile scatterers produce phase separation as in the case of solid state mostly.
We skip here the more strict developments, saving the space for other features, etc.
;;;;;;Laser Physics EM Wave Incident Upon the One, Two and Many Atoms (Nuclei) Matter
It is one of the areas where the clear necessity for multi-body consideration appears via attempts to model the interference of the power laser radiation with the one, or two, and more atoms, nuclei. Which is the known problem not only in the laser physics. We would like to stress our attention onto the more exact expression of this kind of interaction of electromagnetic fields with the particles using more exact formulation and the solution, that still has been done so far for the single electron and a single nucleus.
When intense EM wave (laser radiation) acts upon the piece of a matter, it turned out that under certain circumstances there is a possibility of amplification of the electromagnetic waves when they are going through the matter. To be more specific, laser radiation, going through the plasma, where the processes of the dispersion of the electrons on the nuclei are occuring, may intensify!
The theory of strong electromagnetic radiation is dealing with this problem has been developed in some recent years.
Using the Volkov's solution for wave functions, describing the state of real particles, it's possible to calculate the probabilities of different processes in the field of the EM wave. The mentioned method of calculation of interaction with the intensive field of the wave is used in many researches, as it allows to get general solution's formulae correctly, when there are arbitrary intensions of the wave. This mehod of examination of processes in the intensive electromagnetic field is a half-classic - the falling wave is considered as a classic field, and all the rest of the particles (electron, absorbed and radiated quantum) are considered as via the quantum-mechanics.
We write down the Dirac's equation in the field of the plane EM wave for finding differential cross-sections of radiation and absorption:
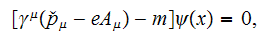
where

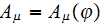 ,
,

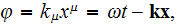

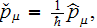 где
где

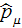 is the impulse operator
component,
is the impulse operator
component,
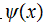 is electron wave function,
is electron wave function,

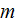 is the electron mass,
is the electron mass,

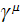 is the Dirac matrix, see more detail in -
is the Dirac matrix, see more detail in -
This equation was first solved by D. Volkov in 1937 and was widely adopted at the beginning of 60-th due to the creation of the laser technology. One of us (V.A.Tsibulnik) used this Volkov's solution models to develop the model for interference of the electron particle colliding with the nucleus resulting fields and the laser EM radiation.
Computing the our task while choosing the 4-potential of the external
electromagnetic field as a sum of two plane waves propagating along the axis

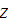 :
:
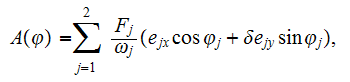
we find to expand the Volkov's solution in this field in a double Fourier series:
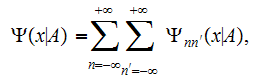
where partial wave functions

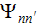 ,
corresponding to various processes of forced radiation and absorption by the
electron the
,
corresponding to various processes of forced radiation and absorption by the
electron the

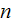 photons of the first wave and
photons of the first wave and

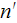 photons of the second wave.
photons of the second wave.
The so-called interference and non-interference areas were studied separately. Interference area is considered as an area where the dispersion occurs in the plane formed by the impulse of the initial electron and the wave vector.
We would like to point out that the given here dependence for the average total differential cross-section dependent on the initial speed of the electron in the interference area as seen in this figure
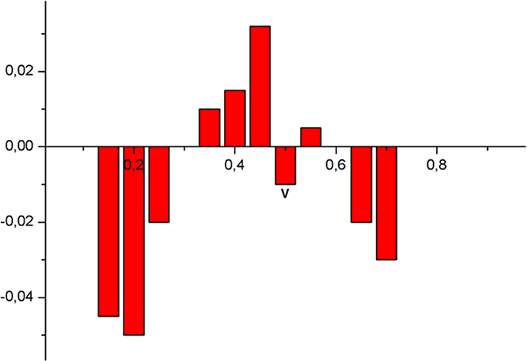
Among results of this analysis we had found that comparison of absolute quantities of the total cross-section in the interference and non-interference areas show that amplification of the electromagnetic waves usually occurs in the interference area and probability of that event almost 3 times higher than the corresponding probability in the non-interference area. In this way it has been shown that for certain conditions the laser rays going through the matter can amplify.
The reason to continue study in this direction is obviously the same - as soon as we have to study and find out the interference picture for not a single nucleus and a single electron, but for the matter of collective interaction of the intense EM radiation with the cloud of nuclei and electrons in the same volume. The correct procedure for development in this field is also using the HSP-VAT.
Two Scale HSP-VAT Solutions of Classical Problems in Many Body, Heterogeneous Media (Hydrodynamics, Wave Mechanics, Electrodynamics etc.).
These classical problems - on straight capillary, single diameter globular morphologies, and 1D layered systems, are already present the examples of pure statements of the test-problem for more then hundred years. Each new generation of researchers trying to solve these problems based on the new tools, but did not obtain a complete solution. Further, the conjugate problem of heat transport in capillary systems has neither been stated fully nor correctly. The studies referred to in this website are the solutions for both scales obtained with the HSP-VAT and provide for the direct and strict communication of physical properties between the both scales.
In all three classical categories of medium morphologies and for many types of physical processes we have achieved the solutions -
These solutions on the Lower Scale are just the same that known to physicists and presented in each university textbook on fundamental disciplines. Meanwhile, the Upper scale solutions could not be obtained with the COHP methods in a previous more than 100 years. What is given for some cases in the university textbooks is the profanation of solutions, are not the correct Upper scale solutions.
The Upper Scale solutions in HSP have been obtained in some cases as exact. Also is important that the Upper Scale classical media solutions for few problems attained in an analytical form, which is unusual so far in HSP-VAT mathematics. The resolution of these questions on the results, meanings, connection of the Lower and Upper scale physical fields, on the balance and conservation of the Lower and Upper scale fields give the sufficient ground to seek the same kind features in the physical problems and their modeling in particle, atomic, nucler, and plasma physics.
Nomenclature

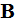 - magnetic flux density
[Wb/m
- magnetic flux density
[Wb/m
 ]
]

 - speed of light in vacuum
- speed of light in vacuum

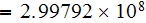

![$[m/s]$](/atom/pic/SSPWebLower1__121.gif)

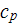 - specific heat
- specific heat

![$[J/(kg\cdot K)]$](/atom/pic/SSPWebLower1__123.gif)

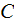 - heat capacity per unit volume
- heat capacity per unit volume

![$[J/(m^{3}\cdot K)]$](/atom/pic/SSPWebLower1__125.gif)

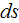 - interface differential area in porous medium
[
- interface differential area in porous medium
[
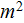 ]
]

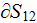 - internal surface in the REV
[
- internal surface in the REV
[
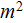 ]
]

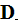 -
electric flux
density [C/m
-
electric flux
density [C/m
 ]
]

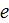 - charge of electron,
- charge of electron,

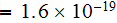

![$[C]$](/atom/pic/SSPWebLower1__134.gif)

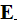 -
electric field [V/m]
-
electric field [V/m]

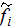

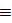

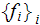 -
VAT intrinsic phase averaged over
-
VAT intrinsic phase averaged over

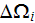 value
value

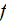

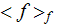 - VAT phase averaged value
- VAT phase averaged value

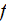 ,
averaged over
,
averaged over

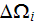 in a REV
in a REV

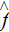 - VAT morpho-fluctuation value of
- VAT morpho-fluctuation value of

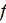 in a
in a


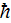 - reduced Planck constant
- reduced Planck constant

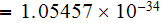

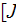

![$s]$](/atom/pic/SSPWebLower1__150.gif)

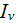 - radiation intensity
[W/(m
- radiation intensity
[W/(m
 sr Hz)]
sr Hz)]

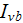 - spectral blackbody intensity
[W/(m
- spectral blackbody intensity
[W/(m
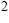 sr Hz)]
sr Hz)]

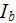 - total blackbody radiation intensity
[W/(m
- total blackbody radiation intensity
[W/(m
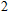 sr)]
sr)]

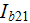 - blackbody specific surface radiation intensity
[W/(m
- blackbody specific surface radiation intensity
[W/(m
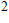 )]
)]

 - current
- current

![$[A]$](/atom/pic/SSPWebLower1__160.gif)

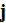 - current density
- current density

![$[A/m^{2}]$](/atom/pic/SSPWebLower1__162.gif)

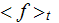 - time averaged value
- time averaged value

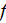

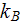 - Boltzmann constant,
- Boltzmann constant,

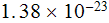

![$[J/K]$](/atom/pic/SSPWebLower1__167.gif)

 - fluid phase thermal conductivity
- fluid phase thermal conductivity

![$[W/(mK)]$](/atom/pic/SSPWebLower1__169.gif)

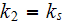 - homogeneous effective thermal conductivity of solid phase
[
- homogeneous effective thermal conductivity of solid phase
[
 ]
]

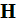 - magnetic field [A/m]
- magnetic field [A/m]

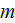 - porosity [-]
- porosity [-]

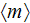 - averaged porosity [-]
- averaged porosity [-]

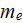 - electron rest mass
- electron rest mass

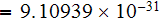

![$[kg]$](/atom/pic/SSPWebLower1__177.gif)

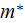 - electron effective mass
- electron effective mass

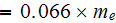

![$\ [kg]$](/atom/pic/SSPWebLower1__180.gif)

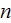 - is the electron number density
- is the electron number density

![$[1/m^{3}]$](/atom/pic/SSPWebLower1__182.gif)

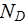 - doping concentration of the active layer
- doping concentration of the active layer

![$[1/m^{3}]$](/atom/pic/SSPWebLower1__184.gif)

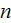 - refraction index [-]
- refraction index [-]

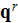 - radiation flux
[
- radiation flux
[
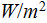 ]
]

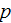 - phase function [-]
- phase function [-]

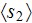 - solid phase fraction [-]
- solid phase fraction [-]

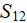 - specific surface of a porous medium
- specific surface of a porous medium

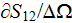 [
[
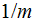 ]
]

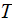 - temperature
- temperature

![$[K]$](/atom/pic/SSPWebLower1__194.gif)

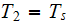 - solid phase temperature
- solid phase temperature

![$[K]$](/atom/pic/SSPWebLower1__196.gif)

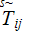 - interface surface temperature when
- interface surface temperature when

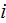 is in upward direction
is in upward direction

![$[K]$](/atom/pic/SSPWebLower1__199.gif)

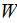 - energy density per unit volume
- energy density per unit volume

![$[J/m^{3}]$](/atom/pic/SSPWebLower1__201.gif)
Subscripts

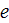 - electron
- electron

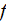

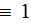 - fluid phase
- fluid phase

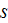

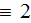 - solid phase
- solid phase
Superscripts

 -
value in fluid phase averaged over the
-
value in fluid phase averaged over the

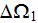

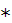 - complex conjugate variable
- complex conjugate variable
Greek letters

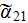 - averaged heat transfer coefficient over
- averaged heat transfer coefficient over

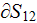

![$[W/(m^{2}K)]$](/atom/pic/SSPWebLower1__212.gif)

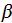 - total extinction coefficient
- total extinction coefficient

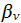 - extinction coefficient [1/m]
- extinction coefficient [1/m]

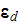

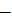 dielectric permittivity [Fr/m]
dielectric permittivity [Fr/m]

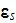

 dielectric permittivity of GaAs
dielectric permittivity of GaAs

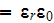

![$[Fr/m]$](/atom/pic/SSPWebLower1__220.gif)

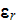

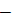 low-frequency relative dielectric permittivity of GaAs
low-frequency relative dielectric permittivity of GaAs

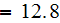

 -
-
![$]$](/atom/pic/SSPWebLower1__225.gif)

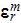

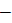 high-frequency relative dielectric permittivity of GaAs
high-frequency relative dielectric permittivity of GaAs

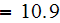

 -
-
![$]$](/atom/pic/SSPWebLower1__230.gif)


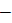 dielectric permittivity of vacuum
dielectric permittivity of vacuum

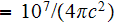

![$[Fr/m]$](/atom/pic/SSPWebLower1__234.gif)

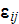 - radiative hemispherical emissivity from phase
- radiative hemispherical emissivity from phase

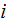 to phase
to phase

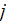 with phase
with phase

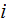 being up into the direction
being up into the direction

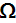

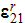 - total radiative hemispherical emissivity from phase
- total radiative hemispherical emissivity from phase

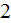 to phase
to phase

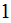 in the REV
in the REV

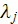 - prescribed Markovian transition length in medium
- prescribed Markovian transition length in medium

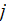 [m]
[m]

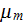 - magnetic permeability
- magnetic permeability

![$[H/m]$](/atom/pic/SSPWebLower1__246.gif)

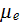 - electron mobility
- electron mobility

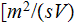

![$]$](/atom/pic/SSPWebLower1__249.gif)

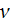 - frequency
- frequency

![$[Hz]$](/atom/pic/SSPWebLower1__251.gif)

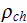 - electric charge density
- electric charge density

![$[C/m^{3}]$](/atom/pic/SSPWebLower1__253.gif)

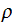 - mass density
- mass density

![$[kg/m^{3}]$](/atom/pic/SSPWebLower1__255.gif)

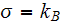 - Stephan-Boltzmann constant
[W/(m
- Stephan-Boltzmann constant
[W/(m
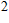 K
K
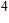 )]
)]

![$[J/K]$](/atom/pic/SSPWebLower1__259.gif)

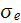 - medium specific electric conductivity
- medium specific electric conductivity

![$[A/V/m]$](/atom/pic/SSPWebLower1__261.gif)

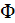 - electric scalar potential
- electric scalar potential

![$[V]$](/atom/pic/SSPWebLower1__263.gif)

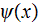 - electron wave function (atomic
physics)
- electron wave function (atomic
physics) 


![$\ ]$](/atom/pic/SSPWebLower1__266.gif)

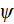 - particle intensity per unit energy (frequency)
- particle intensity per unit energy (frequency)

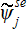 - interface ensemble-averaged value of
- interface ensemble-averaged value of

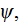 with phase
with phase

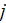 being to the left
being to the left

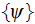 - ensemble-averaged value of
- ensemble-averaged value of

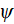

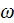 - angular frequency
- angular frequency

![$[rad/s]$](/atom/pic/SSPWebLower1__274.gif)

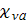 =
=

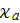 - absorption coefficient
- absorption coefficient

![$[1/m]$](/atom/pic/SSPWebLower1__277.gif)

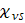 =
=

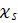 - scattering coefficient
- scattering coefficient

![$[1/m]$](/atom/pic/SSPWebLower1__280.gif)

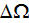 -
representative elementary volume (REV)
-
representative elementary volume (REV)

![$[m^{3}]$](/atom/pic/SSPWebLower1__282.gif)

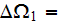

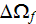 - pore volume in a REV
- pore volume in a REV

![$[m_{3}]$](/atom/pic/SSPWebLower1__285.gif)

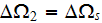 -
solid phase volume in a REV
-
solid phase volume in a REV

![$[m_{3}]$](/atom/pic/SSPWebLower1__287.gif)

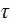 - relaxation time
- relaxation time

![$[s]$](/atom/pic/SSPWebLower1__289.gif)

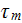 - electron momentum relaxation time
- electron momentum relaxation time

![$[s]$](/atom/pic/SSPWebLower1__291.gif)
References in Solid State Plasmas, Atomic and Sub-atomic Scales Physics:
Steel, M.C. and Vural, B., Wave Interaction in Solid State Plasmas, McGraw-Hill, New York, 1969.
Vorotyntsev, M.A. and Kornyshev, A.A., Electrostatics of a Medium with the Spatial Dispersion, Nauka, Moscow (in Russian). 240 p. 1993.
Travkin, V.S., Catton, I., Hu, K., Ponomarenko, A.T., and Shevchenko, V.G., "Transport Phenomena in Heterogeneous Media: Experimental Data Reduction and Analysis," in Proc. ASME, AMD 233, 1999, Vol. 233, pp. 21-31.
Travkin, V.S. and Catton, I., "Radiation Heat Transport in Porous Media," in Proc. ASME, HTD-364-3, 1999, Vol. 3, pp. 31-40.
Travkin, V.S. and Catton, I., "Tranport Phenomena in Heterogeneous Media Based on Volume Averaging Theory", in Advances in Heat Transfer, 2001, Vol. 34, pp. 1-144.
http://www.travkin-hspt.com/atom/index.htm
http://www.travkin-hspt.com/acoustics/index.htm
http://www.travkin-hspt.com/eldyn/index.htm
Vinogradov, A.P., Electrodynamics of Composite Materials, Moscow, Aditorial URSS, (2001).
Vinogradov, A.P., Physics Uspekhi, 172, No. 3, 363-370 (2002).
Landau, L.D. and Lifshits, E.M., Electrodynamics of Continuous Media. Oxford, Pergamon Press, (1960).
Primak, A.V., Shcherban, A.N. and Travkin, V.S., "Turbulent Transfer in Urban Agglomerations on the Basis of Experimental Statistical Models of Roughness Layer Morphological Properties," in Trans. World Meteorological Organization Conference on Air Pollution Modelling and its Application, Geneva, 1986, Vol. 2, pp.259-266.
Travkin, V.S., Catton, I., Ponomarenko, A.T., and Kalinin, Yu.E., "Bottom Up and Top Down, from Nano-Scale to Micro-Scale, Hierarchical Descriptions of Electrodynamic, Thermal and Magnetic Fields in Ferromagnets and HTSCs", in Proc. DOE 20th Symposium on Energy Engineering Sciences, Argonne National Laboratory, 2002, pp. 296-304.
Travkin, V.S. and I.Catton, Advances in Colloid and Interface Science, 76-77, 389-443 (1998).
Travkin, V. S. and Ponomarenko, A. T., Inorganic Materials, 40, Suppl. 2, S128 - S144 (2004).
Travkin, V. S. and Ponomarenko, A. T., Journal of Alternative Energy and Ecology, No. 3, 9-19 (2005).
Travkin, V. S. and Ponomarenko, A. T., Journal of Alternative Energy and Ecology, No. 4, 9-22 (2005).
Travkin, V. S. and Ponomarenko, A. T., Journal of Alternative Energy and Ecology, No. 5, 34-44 (2005).
http://www.travkin-hspt.com/fluid/03.htm
http://www.travkin-hspt.com/thermph/02.htm
http://www.travkin-hspt.com/eldyn/photcrys1.htm
http://www.travkin-hspt.com/eldyn/glob1.htm
http://www.travkin-hspt.com/eldyn/WhatToDo2.htm
http://www.travkin-hspt.com/eldyn/edeffectivecoeff.htm
http://www.travkin-hspt.com/fundament/homo/homog.htm
http://travkin-hspt.com/fundament/index.htm
http://www.travkin-hspt.com/optics/webdipr/lasopt1.htm
http://www.travkin-hspt.com/atom/04.htm
Travkin, V.S., Nanotechnologies - General Concept for Pretty Large Amount of Pretty Small Gadgets Embedded Into Something and Consequences for Design and Manufacturing, http://travkin-hspt.com/nanotech/index.htm, (2006)
Travkin, V.S., Electrodynamics 2 - Elements 3P (Polyphase-Polyscale-Polyphysics), http://travkin-hspt.com/eldyn2/index.htm, (2013)
Travkin, V.S. and Bolotina, N.N., "The Classical and Sub-Atomic Physics are the Same Physics," http://travkin-hspt.com/parphys/pdf/51_PrAtEd-QM-Ref-2HSPT.pdf, (2013)
Travkin, V.S., Particle Physics - Heterogeneous Polyscale Collectively Interactive, http://travkin-hspt.com/parphys/index.htm, (2011)
Travkin, V.S., Particle Physics (Particle Physics 2). Fundamentals, http://travkin-hspt.com/parphys2/index.htm, (2013)
Travkin, V.S., Nuclear Physics Structured. Introduction, http://travkin-hspt.com/nuc/index.htm, (2006-2013)
Travkin, V.S., What's Wrong with the Pseudo-Averaging Used in Textbooks on Atomic Physics and Electrodynamics for Maxwell-Heaviside-Lorentz Electromagnetism Equations, http://travkin-hspt.com/eldyn/maxdown/maxdown.htm, (2009)
Travkin, V.S., Incompatibility of Maxwell-Lorentz Electrodynamics Equations at Atomic and Continuum Scales, http://travkin-hspt.com/eldyn/incompat/incompat.htm, (2009)
Travkin, V.S., Experimental Science in Heterogeneous Media, http://travkin-hspt.com/exscience/index.htm, (2005)
Travkin, V.S., Statistical Mechanics Homogeneous for Point Particles. What Objects it Articulates? http://travkin-hspt.com/statmech/index.htm, (2014)
Travkin, V.S., Solid State Polyscale Physics. Fundamentals, http://travkin-hspt.com/solphys/index.htm, (2014)
Travkin, V.S., "Two-Scale Three-Phase Regular and Irregular Shape Charged Particles (Electrons, Photons) Movement in MHL Electromagnetic Fields in a Vacuum0 (Aether)," http://travkin-hspt.com/http://travkin-hspt.com/parphys2/abstracts/twoparticlesshort-ab.htm
Travkin, V.S. and Bolotina, N.N., "Two-Scale Two-Phase Formation of Charged 3D Continuum Particles - Sphere and Cube From Electrons in a Vacuum0 (Aether). An Example of Scaleportation of Charge from the Sub-Atomic to Continuum Charged Particles, Conventional MD Cannot be Applied," http://travkin-hspt.com/http://travkin-hspt.com/parphys2/abstracts/subtocontin-ab.htm
Travkin, V.S. and Bolotina, N.N., "One Structured Electron in an Aether (Vacuum0) Electrodynamics, Many Electrons in an Aether Fixed in Space - the Upper Scale Galilean Electrodynamics ," http://travkin-hspt.com/http://travkin-hspt.com/parphys/abstracts/stillelectrons-ab.htm
Travkin, V.S. and Bolotina, N.N., "Electrons and CMBR (Cosmic Microwave Background Radiation) Flux of Photons in a Vacuum0 (Aether) - Two-Scale Galilean Theory ," http://travkin-hspt.com/parphys/abstracts/elcmbr-ab.htm
and in publications mentioned above.
![]()
With time, more topics will be uploaded into this and neighboring sub-sections for education and for advertisement.