We consider the incidence of the TE type (s-polarized) wave from the upper half-space with the dielectric permittivity onto the lower subspace with the heterogeneous medium of 100 or 200 or even bigger number (600) of layers, consisting of homogeneous, with constant coefficients layers of two kinds, or inhomogeneous layers of two kinds when each layer of each kind has the nonlinear dependency of material's electric properties.

The system of layers: with - dielectric permittivity of the odd layers, - dielectric permittivity of the even layers; - thickness of i-th layer; - coordinate of the upper boundary of the -th layer; where is the layers pack's upper boundary z-coordinate.

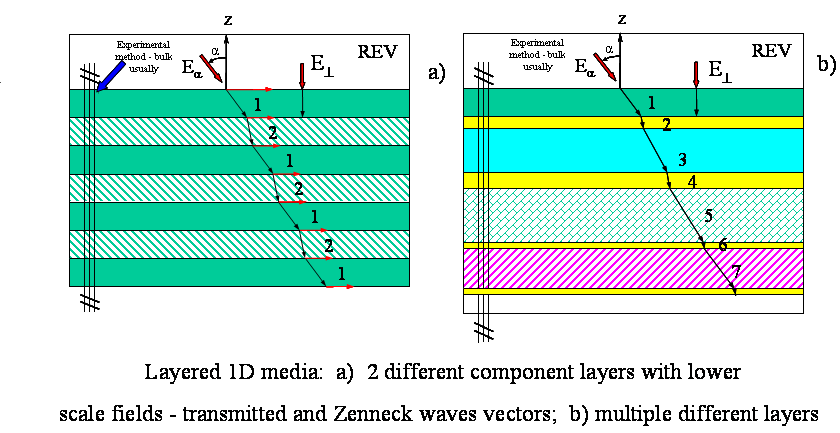
The statement with nonlinear properties has the much more complicated lower and Upper scale governing equations.

On the lower physical scale we have to use the Helmholtz equations for the upper half-space region

where - the wave vector of the incident wave.

For the lower region with the superlattice the lower scale medium for each layer of kind 1 or 2 we can write:

1) First period - two layers -

and

with the conjugate boundary conditions of the IV-th kind BC's as like in thermophysics. The two fields are having in the interface surface the BC's, for example, when the phase 1 contacts with the phase 2, then for the tangential components of the electric field should be

while the second BC appears from the condition for magnetic fields due to Amper's law

which implicates that

where the subscript means - the interface.

For the 2D case we have, for example, the TE polarized in direction -

So, anyway the tangential component will lay on the interface surface and the second BC will be the same.

While for the bottom interface surface of the 2 layers period we have the BC's

connecting fields to the following period. And for the all other periods the same mathematical statements occur.

The Upper Scale VAT Governing Equations

In linear case, when conductivity coefficient then the VAT equation in phase one simplifies to

when we also have from the lower scale

In the phase two the Upper scale governing equation is

We provided the few situation solutions for this two-scale problem in the subsection -

"Electodynamics/Two Scale EM Wave Propagation in Superlattices - 1D Photonic Crystals" -

and in another subsection -

"Optics/Photonic Crystals and Their Modeling" -

Here we are interested in formulation of the definitions for the Two-scale properties for this problem. As usual, the one scale properties while often written as for local, point specific homogeneous one scale statement, in reality being implied as for the volumetric, averaged definitions for fields or their derivatives.

Will be added more to the public domain from the proprietary one regarding this topic.