Cross-Characteristics Modeling Explained in Terms of VAT

The whole matter of what is appeared to be called as the cross coefficient theoretical development for the momentum transport - electric field processes until now is based solely on the mathematical similarities in description of velocity (creeping) and electrical potential fields in a fluid phase located in an insulating porous solid phase. According to this approach, initially suggested by Johnson et al. (1986) the dependency for fluid static permeability in porous media can be written as

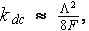
where is the special parameter which relates a pore volume -to - surface in porous medium and estimates through the known electrical field E=(r) which is in turn found through an electrical potential .

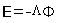The electrostatic potential field 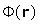is known to be described by the Laplace equation inside of the fluid volume 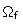with the boundary conditions. The formation factor F is determined through the relationship (see, for example, Achdou and Avellaneda, 1992; Avellaneda and Torquato, 1991)

The medium with straight nonintersecting, randomly oriented, cylindrical capillaries with random diameters has (Achdou and Avellaneda, 1992)

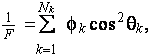
which is only being such simple result because of nonpolarizable boundary condition on the capillaries wall. Corresponding length scale suggested in work by Johnson et al. (1986) estimates through

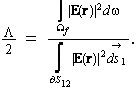
The way in which the electrical field quadratic absolute function appeared in volumetric and surficial integrals is worth to describe in more detail. First, consider the transformation of the main conductivity equation (taken as to be for a homogeneous medium) as through the inclusion of the one more factor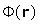

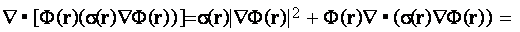
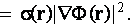
If then this identity is the subject of integration over the fluid volume of the problem to which the voltage drop 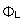is applied, then by the Gauss-Ostrogradsky's theorem of divergence the formula for effective conductivity will be justified (Johnson et al., 1986; Bergman, 1978) following the transformation for steady-state problems

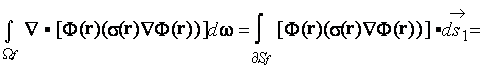
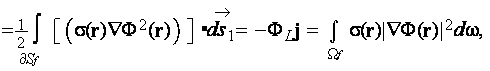(1)

while the left hand side of this expression should be transformed to

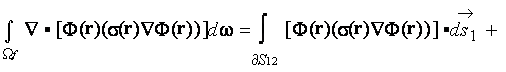
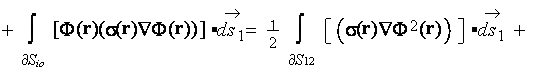
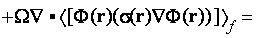
where 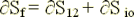is the whole surface bounding the fluid volume 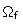, and 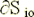is the surface of input and output of 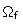in the .

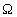As one can see in the development of (1) the averaging theorem

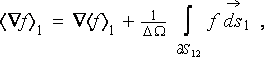
was not being accounted, which means the major departure from heterogeneous spacial differentiation rules established through the VAT theorems. Note, that the averaging here considers to be performed over the entire volumes used for the stated problem 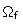, meaning that this averaging use the REV equals to which has something in common with the VAT intended averaging procedures.

Avellaneda and Torquato (1991) shown the peculiarities of the mathematical solution for the transient Stokes equations while connecting the fluid permeability k_dc and formation factor F using the employment of solution decomposition for eigenfunctions 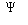and using decomposition of the constant unit vector e to seek the electrical field solution E. By presenting the fluid permeability k_dc through the series distributed solution in the 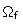the formula for permeability in porous media was established. As it is obvious from the algorithm and description of the found dependency for permeability k_dc and two suggested parameters L (or ) and F and is clear that the porous medium flow problem was brought down with the help of the two following techniques:

1) Eigenfunction solutions which employ the Poisson type equation infinite series solution;
and
2) Full scale Laplace equation solution for electric field E in the fluid phase .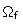

It is worth to note here that the full problem solution of either one of these tasks only once does provide an actual complete solution for the entire closure problem together with solution for the VAT based porous medium fluid and electrostatic transport problem, and many other statements, (see, for example, Travkin and Catton, 1998,2001) and gives much more information in terms of overall behavior of a problem than the DMM-DNM solution

Another reality, as was shown by Achdou and Avellaneda (1992) is that if in the medium which posses the real morphological features - as angles and steep curves of an interface surface - the problem of correspondence of k_d to L (or ) and F falls apart, and primarily due to physics of phenomena. They studied the influence of pore roughness on the dynamic and static permeability of single pore and found out, that "even if, in reality, wedge like singularities are rounded off microscopically, large curvatures on the pore surface will produce strong surface concentration of the electric field". As we will see below exactly these features are fully incorporated into the scaled VAT modeling and simulation equations.

Also, they concluded that "with regard to pore-size dispersion, it is clear that a theory based on a single-tube response function (as for the dynamic permeability k_ac see Johnson et al., (1987), Sheng and Zhou (1988) will be inadequate if the dispersion is wide enough".

An exact flow resistance results obtained on the basis of VAT based governing equations in work by Travkin and Catton (1999) for the random pore diameter distribution for almost the same morphology as was used by Achdou and Avellaneda (1992). The distribution of flow resistance exposed the wide departure from the Darcy law based treatments with constant coefficients. That was shown even for the morphology where a single pore exists with diameter different from the all others. Meanwhile, using the VAT based procedures (Travkin and Catton, 1998;1999) one can easily develop the needed variable, nonlinear coefficient of permeability for a Darcy dependency when fluid flow is Stocksian

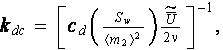
where the coefficient of overall resistanse to momentum transport c_d derived for this particular morphology on the basis of exact analytical (in laminar regime) or well established correlations for Fanning friction factor in pore for other flow regimes. In this exact formula S_w is the specific surface of the porous medium and 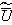is the intraphase averaged velocity of the fluid, which can be of any regime - laminar, turbulent or intermediate.

Wong and Pengra (1995) made an attempt for justification of using electrokinetics cross-phenomena as the rigorous one and that was reported as a theoretically well proven fact. Authors consider the Onsager's reciprocal relations in the form

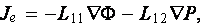
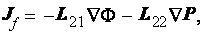
where L₁₁ =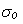 is the no-pressure gradient conductivity of the saturated porous medium, and 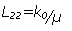is the zero-electric-field permeability of the same medium. Deducing further the formula connecting the three transport coefficients (effective electrical conductivity of the brine saturated rock 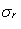, streaming potential coefficient K_S and electroosmosis coefficient K_E) authors note - "the significance of this analysis is that it shows that the pore radius and permeability can be rigorously determined by measuring the K_S, K_E and the conductivity . 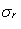This result is completely independent of any microscopic detail of the pore structure and does not rely on any empirical correlation". Meanwhile, this result is the complete mathematical consequence of the assigned linear dependencies in the Onsager's kinetic relations which are generally speaking only experimentally determined at low intensity regimes for conductivity and permeability coefficients and strictly not justified theoretically.

That means also, if coefficients L_ij in Onsager's relations would be taken according to more exact basis the whole problem becomes nonlinear and with the strong dependency on morphology of the medium. As, for example, even for the simple morphology of straight parallel capillaries with random diameters the coefficient L₂₂ equals to

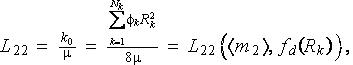
where f_d(R_k) is the probability density function of the pore radius ensemble.

REFERENCES

Achdou, Y. and Avellaneda, M., "Influence of Pore Roughness and Pore-size Dispersion in Estimating the Permeability of a Porous Medium From Electrical Measurements," Physics of Fluids, A, Vol. 4, pp. 2651-2673, (1992).

Avellaneda, M. and Torquato, S., "Rigorous Link Between Fluid Permeability, Electrical Conductivity, and Relaxation Times for Transport in Porous Media," Phys. Fluids, Vol. 3, pp. 2529-2540, (1991).

Bergman, D.J., "Dielectric Constant of a Composite Materials - Problem in Classical Physics," Phys.Rep., vol. 43, No. 9, pp. 378-407, (1978).

Johnson, D.L., Koplik, J., and Schwartz, L.M., "New Pore-size Parameter Characterizing Transport in Porous Media," Phys. Rev. Lett., Vol. 57, No. 20, pp. 2564-2567, (1986).

Johnson, D.L., Koplik, J., and Dashen, R., "Theory of Dynamic Permeability and Tortuosity in Fluid-Saturated Media," J. Fluid Mech., Vol. 176, pp. 379-402, (1987).

Sheng, P. and Zhou, M.Y., "Dynamic Permeability in Porous Media," Phys. Rev. Lett. 61, pp. 1591-1594, (1988).

Travkin, V.S. and Catton, I., "Porous Media Transport Descriptions - Non-Local, Linear and Nonlinear Against Effective Thermal/Fluid Properties", in Advances in Colloid and Interface Science, Vol. 76-77, pp. 389-443, (1998).

Travkin, V.S. and Catton, I., "Nonlinear Effects in Multiple Regime Transport of Momentum in Longitudinal Capillary Porous Medium Morphology", J. Porous Media, Vol. 2, No.3, pp. 277-294, (1999).

Wong, P.-Z. and Pengra, D.B., "Pore Size, Permeability and Electrokinetic Phenomena," in Access in Nanoporous Materials, T.J. Pinnavaia and M.F. Thorpe, eds., Plenum Press, New York, pp.295-317, (1995).