and for experimental HSP-VAT procedures in

that the treatment of the effective coefficient issues must be done with the full two scale equations of the HSP-VAT problem taken into consideration.

There are number of reasons why we can not get along doing the same stuff in the HSP-VAT effective coefficient determination as in the homogeneous physics usually done for a long time.

As long as not every HSP-VAT electrodynamics equation and definition has been published we make here a great deal of attention and provide few examples with the works and expressions derived with the elsewhere written mathematics, as this is done in the subsections -

Cross-Characteristics Modeling Explained in Terms of VAT

When the 2x2 is not going to be 4 - What to do?

Two Scale EM Wave Propagation in Superlattices - 1D Photonic Crystals.

We start with the homogeneous followed by heterogeneous formulation for the effective coefficient as in

When the 2x2 is not going to be 4 - What to do?

Few the very important HSP-VAT statements developed above should be reiterated here -

4) The upper (the second) scale solutions are not achievable in brackets of homogeneous physics. There are no definitions and mathematics (at least correct ones) for that in homogeneous physics. That is why there is continuous search for experimental methods to measure the superlattice conductivity and dielectric permittivity. For example, most of the latest heat conductivity measurement methods use the transient try-and error fitting techniques to match the measured bulk data while solving the lower scale homogeneous transient heat conductivity equations. They calculate in this way the different - the TRANSIENT homogeneous bulk heat conductivity coefficient. That coefficient differs from a steady-state sought heterogeneous effective coefficient. Also, with these techniques there is no way to find out the Phase Effective Coefficients of conductivity or permittivity.

7) The dependencies outlined in homogeneous physics solutions are incorrect if being applied with the exact fields for the lower scale solutions as, for example, the homogeneous formula gives the displacement field in the system through the averaged electric fields (potentials)

and this value can be tens and hundreds times different from the correct one. We are assuming here as usual that according to homogeneous Gauss-Ostrogradsky theorem the following is true - the averaged over the each phase gradient operator acting on the potential function is equal to

which is incorrect!

8) The known "classical" formulae for "in-series" two phase 1D composite effective coefficients can be calculated as known for bulk values only for linear problem. It is important to say that the formula for the linear effective bulk coefficient

is correct, but is not valid for the derivation! Final result and the formula is correct, but the derivation is not correct ? It can not be derived even for linear problem when applied only the one scale homogeneous knowledge base.

That is because in spite that the homogeneous fields formula is correct.

9) The simple particular layered morphology of the two-scale problem dictates the peculiarities of the physical phenomena involved. Thus, for the linear problem there are the two physical mechanisms involved in field's transport - 1) is the INTRAPHASE, in each phase; and 2) is the INTERFACE transport. In most common situations those are the three different components in the transport characteristics. The later properties described and accounted for as to the physical phenomena seems only in chemistry, chemical technology.

In electrodynamics it is still considered as the 3D phenomena of a one scale.

11) The mathematical formulation and exact calculation of the surficial transport components gives an expected explanation of decreased overall bulk permittivity and what is more important is of their magnitudes. It also allows to compare transport in each separate phase along with their components.

12) Needless to say, that the unknown component of interface transport can reach values of hundreds and even thousands percent of effective bulk values - see Figs. 2,3 in -

When the 2x2 is not going to be 4 - What to do?

That can be directed toward the explanation of some known physical phenomena as, for example, like the interface resistance and polarization among others.

From numerous works on effective coefficients for electrodynamic problems we can select just few, no matter of whom, but rather of known people and see - what is considered as an "effective" coefficient when homogeneous GOT being used and applied for this when the media are Heterogeneous.

For example, in the paper by Tao et al., (1990) we see a good solution of the same kind of model - the homogeneous One scale commonly known mathematical model for a heterogeneous media of the two kinds

which we see in the page 2419.

As we analyze below the one of the best studies of effective coefficients problem done by Kushch, these coefficients in work Tao et al. (1990) (and in other lower scale homogeneous models) nothing more as the quazi-"effective" one scale coeffiicents. They are not correctly averaged characteristics.

But what about the experiements assessment, more or less good comparisons and such in homogeneous electrodynamics - one would ask?

Well, the problem also is with the experimental set up. It is also done with the same theoretical ground of Homogeneous conseptions - so, What else you would expect in return ?

In the next paper by Bergman and Dunn (1992) in the p.13262 we can read about calculations of the effective dielectric permittivity in the previous work -"In practice, the results for were often not better than those found by using the simple Clausius-Mossotti or Maxwell-Garnett (MG) approximation, which ignores almost all the details of the microgeometry."

We would say - And not only of microgeometry, but principally is of not averaged fields, simply incorrect.

Also in that page 13262: "In this article, we propose another method for calculating of such composites in the quasistatic regime. Our method also uses the Fourier coefficients of at reciprocal-lattice values of and is therefore applicable to quite general, periodic microgeometries. "

That is incorrect statement as we see in many places of this website. This is the same Lower scale "quasi-averaged" "effective" coefficient see also in -

and for experimental HSP-VAT procedures in

For a problem of multilayer cross applied electric field Bergman et al. (1994) wrote the equations which right hand side is of the local determination

where variables and are said to be the local values, while is the nonlinear function!

At the same time the next equation is written for the nonlocal averaged fields as

where and are the volume fractions of the metal and dielectric phases. This last expression instantly substituted with the locally written dependency

as for

This mix of locally defined and non-local variables makes the further analysis useless.

In the abstract of the paper done by Busch and Soukoulis on the mean, effective transport properties of heterogeneous media they wrote, p. 3442 - "We present a new method for efficient, accurate calculations of transport properties of random media. It is based on the principle that the wave energy density should be uniform when averaged over length scales larger than the size of the scatterers. This scheme captures the effects of resonant scattering of the individual scatterer exactly, as well as the multiple scattering in a media-field sense." (?)

"It has been successfully applied to both "scalar" and "vector" classical wave calculations. Results for the energy transport velocity are in agreement with experiment. This approach is of general use and can be easily extended to real different types of wave propagation in random media."

Else in p. 3442 - "In the present Letter, we present a new approach in calculating the transport properties of random media that takes into account the multiscattering interactions in a mean-field sense."

Meaning for the Averaged Electrodynamics Fields. In the page 3443 - "For scalar waves the energy density is

whereas the energy density of the vector waves is given by

note, that these fields are not averaged !

When one would average this equality to get to the definition of average energy density field one needs to have averaging for the nonlinear function in the r.h.s. of the above equalities. They are nonlinear - meaning that is why we get unusual results.

The main idea of transforming the real multiphase medium to an "effective" one seen from this representation of that transformation

The reader of this website needs to keep in mind - that no matter what authors of this or other works saying about their "mean", "averaged", "bulk" characteristics calculated or assessed with the use of GOT, which is in ALL the cases in Homogeneous physics they do so, the effective, averaged characteristics SHOULD satisfy at least this equation for the simplest situation with the phase constant coefficients (for dielectric permittivity, for example)

meaning you need to know the averaged fields AND the interface field.

They write also in the same p. 3443 - "The polarization of the EM waves has to be taken into account on a fully vector calculation in deriving the Boltzmann equation, starting from the Bethe-Salpeter equation." (?)

"This is still the outstanding problem of the field."

Which is wrong - regarding the derivation of good, correct transport equation in heterogeneous media electrodynamics which should take into account the many separately known physical effects in these media, also - see our analysis on scattering modeling practices in acoustics -

and in Optics -

In one of HSP-VAT formulations the bulk dielectric permittivity effective coefficient for the two phase medium we can calculate as via

where as we defined above

Writing here few basic formulae for the dielectric medium statement which usually utilized while applying the Detailed Micro-Modeling - Direct Numerical Modeling (DMM-DNM) for a heterogeneous medium on the Lower Scale

where the dielectric coefficient is the piece-wise function

and is the characteristic function of phase . Interface boundary conditions assumed for this statement are

The mathematical statement in the DMM-DNM approaches usually deals with the local fields and as soon as the boundary conditions are determined in some way, the problem became formulated correctly and can be solved exactly.

Difficulties arise when the result of this solution needs to be interpreted - and this is in the majority of problem statements in heterogeneous media, in terms of non-local fields, but averaged in some way. The averaging procedure usually is proclaimed in one of the fashions - either doing stochastic or spatial, volumetric integration. Almost all of these averaging developments are done incorrectly due to disregard of averaging theorems for differential operators in heterogeneous medium.

Secondly, as soon as the boundary surfaces are intersecting both of the phase subvolumes, the conventional boundary conditions become invalid as well as the DMM-DNM solution. In the event when boundary surfaces are chosen to belong to only one of the phases in a random or irregular morphology medium the problem becomes formulated as in a special kind of periodic medium and its solution has peculiarities and useful value for the problem stated only with the one phase boundary condition. When a problem's physical model includes phenomena of wave propagation through the boundary of heterogeneous body as, for example, in most of electromagnetic problems, the one phase boundary condition has no value for that problem.

Meanwhile, if the coefficient of dielectric permittivity in the phase one is a constant value then the upper scale VAT equation for potential field in this phase is

The steady-state equation in the phase one in terms of potential flux when is a constant looks like

and in the second phase the same kind of potential equation

Observing these equations one can assume that the effective permittivity coefficient in a medium should come from the equation of sum of the previous equations for each phase which can be reduced consecutively accounting for the conservation of displacement field at the interface

then we can summarize

or

which results in

because and also the same kind of expression can be obtained

assuming that the phase two is the globular inclusions phase. Standard definition for effective (macroscopic) permittivity (or conductivity) tensor determines from the following equation

in which assumed that the displacement field vector can be presented as

as soon as for the standard BC

because

and

Further, we assume that

and, for the usually assumed at the interface physics the effective coefficient determines as

	(1)

or

or

involving knowledge of the three different potential functions and in the upper scale space consideration in the volume and at the interface This formula for the steady state effective permittivity can be shown is equal to the known expression

which means, when applied the WSAM theorem for averaging the operator then is equal to

This is one of the evidences that for some (very few) instances there can be drawn the direct analytical comparison of homogeneous and heterogeneous formulae. For this particular above formula the comparison shows the coincidence. We will demonstrate below for the layered medium one more example of a complete inheritance and conjugation for homogeneous and heterogeneous descriptions.

It is worth to note here that the known formulae for the effective dielectric permittivity (or conductivity) of the layered medium

for electric field applied in parallel to interface of layers, and

when an electric field is perpendicular (in-series) to the interface, can be derived from the general expression (1) but only for linear medium (constant coefficients).

The following is the analysis of outstanding work by one of the workers who while having familiarity with the HSP-VAT had done the study with the wrong application of the homogeneous GO theorem, regarding the effective coefficient finding.

In his work Kushch (1997a) described in some misleading text pieces the mathematical procedure for calculation of the effective coefficients of conductivity (dielectric permittivity, diffusivity, etc.) in globular media. In pages 67 and 70 author described few main points in assessment (simulation) of the thermal bulk effective conductivity for the two-phase composite with spherical inclusions as a second discontinuous phase.

Doing that, author firstly included in his text some elements of VAT, for example, on page 70 is given the formula for the component of bulk thermal flux

with the surface integral. This combination of the surface integral and averaged temperature gradients in each of the phases could appear in the formula only because of heterogeneous WSAM theorem. But not because of the use of the homogeneous GO theorem. Author does not tell about this feature to a reader.

Author intentionally avoiding using the VAT language, for example, in equation (2.2)

and while writing formulae (4.1), (4.2)

he does not tell that those two groups of definitions are from different spaces. That is - his effective coefficient is applicable to the only condition of a thermal equilibrium for both phases, when the steady-state thermal circumstances have been established, see more explanation in Travkin (1998, 2001a,b) (2001a - Travkin, V.S., "Discussion: "Alternative Models of Turbulence in a Porous Medium, and Related Matters" (D. A. Nield, 2001, ASME J. Fluids Eng., 123, pp. 928--931)," J. Fluids Eng., Vol. 123, pp. 931-934, (2001a)).

Author also does not tell to a reader - How the "average gradient" is described mathematically for the two-phase matter, while it is very important for assessments and analysis of few "effective" coefficients existing for this problem.

Starting with the volume integration of the heat flux as in

which is in VAT notations

and using only the GO homogeneous medium theorem like

where the normal vector is directed outward from the solid-fluid (particle-matrix) phase interface surface Kushch derived on page 70 for the regular globular inclusions composite using the declaration that the formula for the effective coefficient of conductivity as for the one (in z) direction has to be

which according to equality of temperatures at the

gives

and further Kushch "obtains"

	(2)

referring to the GO theorem when doing spatial integration over the particle ( with the more often used in western literature notation for coefficient of thermal conductivity ) he gets

and what is the most interesting is the integration over the matrix (fluid) phase sub-volume

; with which is according to usual GO theorem should looks like

but which should be done according to WSAM theorem as

	(3)

Now, let we try to obtain the same (2) from the initial fluxes integration equality

and following the derivation path recommended by Kushch. Then we get

and which is obviously not going to coincide with the Kushch's (2) ?

To go to the real derivation path used by Kushch we need to use the (3) which is using the WSAM theorem and getting

Meanwhile, this expression is still not the same as (2) ?

We need to go deeper into the mathematics hidden in the paper by Kushch (1997) intentionally. Why he did that?

Because he did not want to show the HSP-VAT derivation path and averaging VAT notations, refer to the new to him at that time (94-96) VAT modeling and scaled averaging mathematics, thus doing gaps in the mathematics derivation and in the explanations of the resulting formulae.

Still, we need, first of all, the few explanations following the WSAM theorem's consequences.

The above derivations are possible because for the matrix phase as soon as according to the GO theorem we have the equality

where is the surface of entrance and exit for the phase-f at the boundary surface of the REV suggested by Kushch so further we have according to the WSAM theorem that the surface integral over the input-output surface is equal

then, substituting this equality into the previous regular homogeneous GO theorem based formula we have

dividing this expression's both side parts by we get

or

We need to show further that we can not get this equality (2) using only the homogeneous medium GO theorem.

To show this, let we start from the general correct (with the used WSAM theorem) formula for the effective conductivity coefficient in the two-phase linear heterogeneous medium (constant properties)

and realizing that the morphology of the medium and the REV does not connect the solid phase to the bounding REV surface when that for the specifically carved in this work REV (on p. 70 - "For a periodic composite the elementary structure cell, in the form of a parallelepiped with sides containing one particle, can be chosen as the representative volume.")

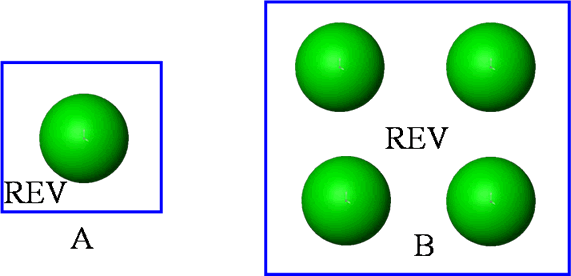
with the external particle-matrix interphase surface equal to zero

That means using the WSAM theorem and keeping in mind that we have the only this arrangement for the REV we can write

as soon as though we have that

and that means - we can get right for this case, when the REV has the spatial location as it does not intersect with the solid phase - the spheres, the equality which is

	(4)

So, these are the reasons why Kushch used the formula for the effective conductivity in only such a form (2).

But it is unrealistic - to have only such a special REV's locations, right ? This means - the case sensitive only partial solution has been obtained.

And generally this is not the full formula for this coefficient. As long as we can have the real general legitimate arrangements - when the REV's would intersect the both phases -

Then, that means we need to use the general formula for the steady-state effective conductivity coefficient followed from the WSAM theorem

and use the same algorithms as we used for the superlattice coefficient !

This formula above (2) (by Kushch (1997a)) for the REV with the external surface going through the matrix (fluid) only (with the inclusions inside)

still should be written

so - it can be written also as

with the one differential term: at the r.h.s.!

This is the very important distinction from the formula by Kushch (2).

But Kushch did this because the part of the sum (4) is equal to zero, and that gave him the ability to use the generalized formulae for the effective coefficients, using the general averaged gradient .

At the same time he explained nothing in the paper (Kushch, 1997a) about the WSAM theorems that only gave him a chance (comparing to his previous studies on the same topic - Kushch, 1991, 1994, and other studies on composites elasticity and strength) to make this research possible !? Still, with the wrong Effective Coefficient tables - because the final averaging formulae had been done incorrectly.

Summaries:

From this lengthy analysis we can get at least three useful conclusions.

1) First is that the all effective coefficients obtained for heterogeneous media with mathematics based on the homogeneous GO theorem give incorrect results!

This is the pretty strong message and I will use it with all my respect to the authors of those incorrect studies and for a while. For example, the excellent DMM-DNM study by Cheng and Torquato (1997) done for kinds of medium as

then, when the results of DMM-DNM of the Lower scale applied toward the obtaining the effective coefficient the assessments would give incorrect outcome due to the reasons we pointed to above.

2) The second conclusion is that even the usage of WSAM theorem, but incorrectly, as done by Kushch (1997) brings out the incorrect effective coefficients also !

3) What is the difference, the correction to the homogeneous Lower Scale "effective" coefficients to get to the sought after the Heterogeneous Upper Scale effective coefficients? This is the subject of each specific problem consideration and of the two scale solution.

References:

Bergman, D.J. and Dunn, K.-J., "Bulk Effective Dielectric Constant of a Composite with a Periodic Microgeometry," Physical Rev. B, Vol. 45, No. 23, pp. 13262-271, (1992).

Bergman, D.J., Levy, O., and Stroud, L., "Theory of Optical Bistability in a Weakly Nonlinear Composite Medium," Phys. Rev. B, Vol.49, No. 1, pp. 129-134, (1994).

Busch, K. and Soukoulis, C.M., "Transport Properties of Random Media: A New Effective Medium Theory," Phys. Rev. Lett., Vol. 75, No. 19, pp. 3442-3445, (1995).

[8] Fokin, A.G. Macroscopic Conductivity of Random Inhomogeneous Media. Calculation Methods//Physics - Uspekhi. 1996. V. 39, N. 10. P.1009-1032.

[11] Cheng, H. and Torquato, S. Electric-field Fluctuations in Random Dielectric Composites//Phys. Rev. B. 1997. V. 56, N. 13. P. 8060-8068.

[50] Kushch, V.I., "Conductivity of a periodic particle composite with transversely isotropic phases," Proc. R. Soc. Lond., A 453, pp. 65-76, (1997a).

Kushch, V.I. and Artemenko, O.G., "Determination of Temperature Field in a Granular Layer," Doklady AN Ukr. SSR, No. 3, pp.74-77, (1983), (in Ukrainian).

Kushch, V.I., "Stressed State and Elastic Moduli of a Periodic Composite Reinforced By Coated Spherical Particles," Mechanics of Composite Materials, Vol. 29, No. 6, pp. 816-822, (1993), (in Russian).

[51] Kushch, V.I., "Microstresses and Effective Elastic Moduli of a Solid Reinforced by Periodically Distributed Spheroidal Particles'', Int. J. Solids Structures, Vol. 34, No. 11, pp. 1353-1366, (1997b).

Kushch, V.I., "Heat Conduction in a Regular Composite With Transversely Isotropic Matrix," Doklady AN Ukr. SSR, No.1, pp.23-27, (1991), (in Ukrainian).

Kushch, V.I., "Thermal Conductivity of Composite Material Reinforced by Periodically Distributed Spheroidal Particles," Engng.-Phys. Journal, Vol. 66, 497, (1994), (in Russian).

Kushch, V.I., "Elastic Equilibrium of a Medium Containing Finite Number of Aligned Spheroidal Inclusions," Int. J. Solids Structures, Vol. 33, No. 8, pp.1175-1189, (1996).

Golovchan, V.T., Guz', A.N., Kokhanenko, Yu.V., and Kushch, V.I., Mechanics of Composites. T.1. Statics of Materials, Kiev, Naukova Dumka, 1993, 455pgs, (in Russian).

Tao, R., Chen, Z., and Sheng, P., "First-Principles Fourier Approach for the Calculation of the Effective Dielectric Constant of Periodoc Composites," Phys. Rev. B, Vol. 41, No. 4, pp. 2417-2420, (1990).

[33] Travkin, V.S. and Catton, I., "Porous Media Transport Descriptions - Non-Local, Linear and Non-linear Against Effective Thermal/Fluid Properties// Advances in Colloid and Interface Science," Vol. 76-77, pp. 389-443, (1998).

Travkin, V.S., "Discussion: "Alternative Models of Turbulence in a Porous Medium, and Related Matters," (D.A. Nield, 2001, ASME J. Fluids Eng., 123, pp. 928-931)," J. Fluids Eng., Vol. 123, pp. 931-934, (2001a).

Travkin, V.S. and Catton, I., "TRANSPORT PHENOMENA IN HETEROGENEOUS MEDIA BASED ON VOLUME AVERAGING THEORY", in Advances in Heat Transfer, Vol. 34, pp. 1-144, (2001b).

Travkin, V. S. and Ponomarenko, A. T., "Electrodynamic Equations for Heterogeneous Media and Structures on the Length Scales of Their Constituents", Inorganic Materials, Vol. 40, Suppl. 2, pp. S128 - S144, (2004).

Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications -1," Journal of Alternative Energy and Ecology, No. 3, pp. 7-17, (2005).

Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 2," Journal of Alternative Energy and Ecology, No. 4, pp. 9-22, (2005).

Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 3," Journal of Alternative Energy and Ecology, No. 5, pp. 34-44, (2005).