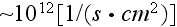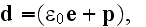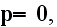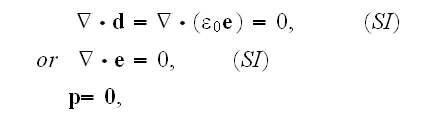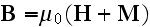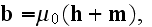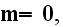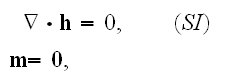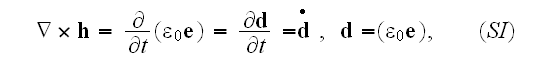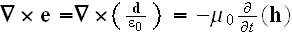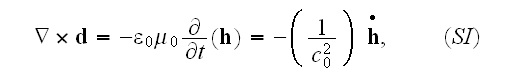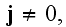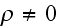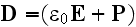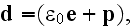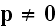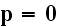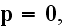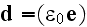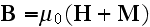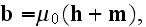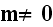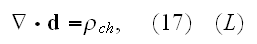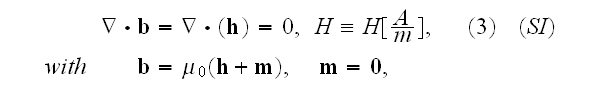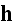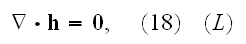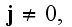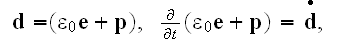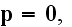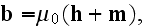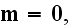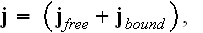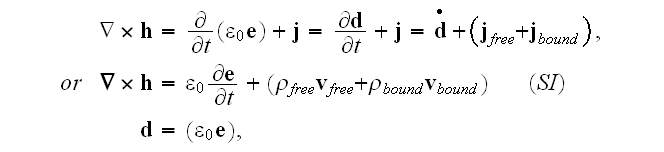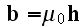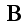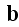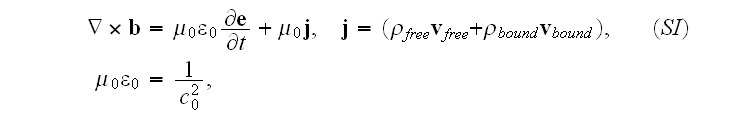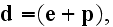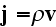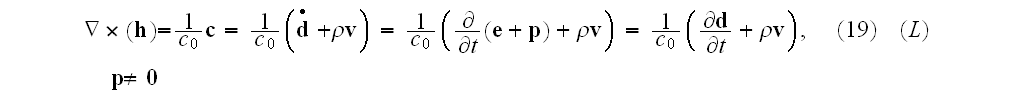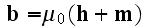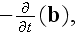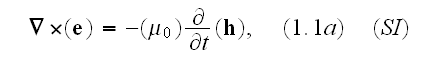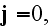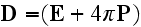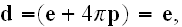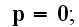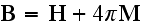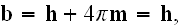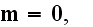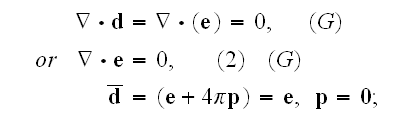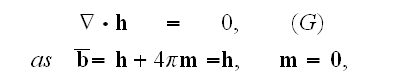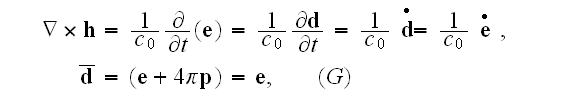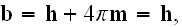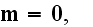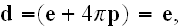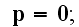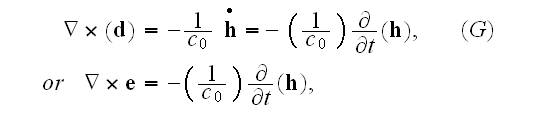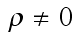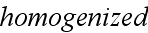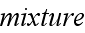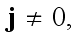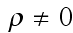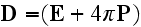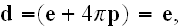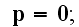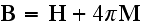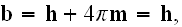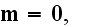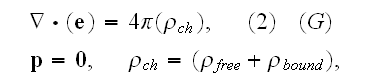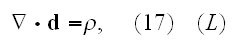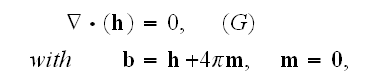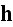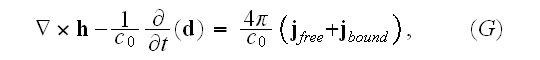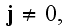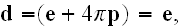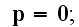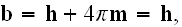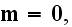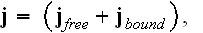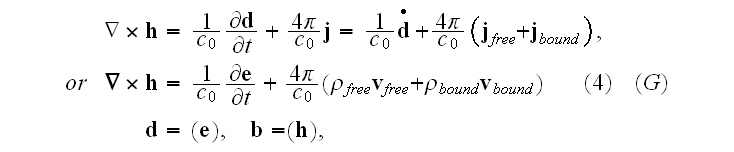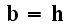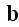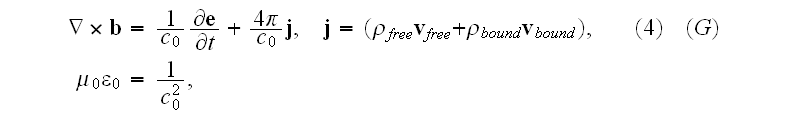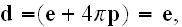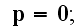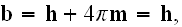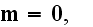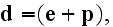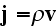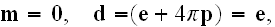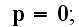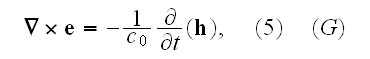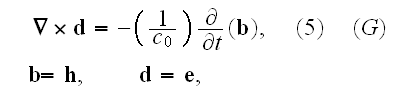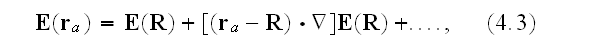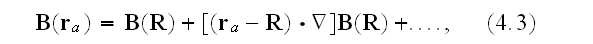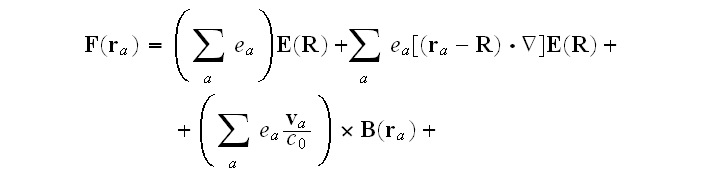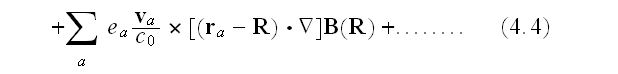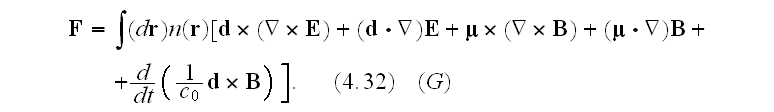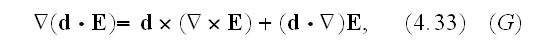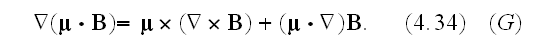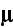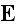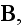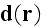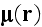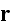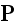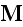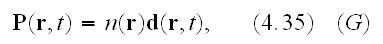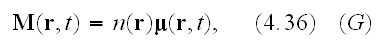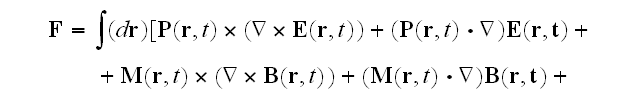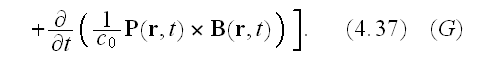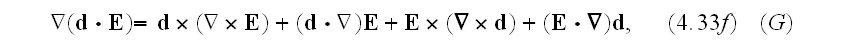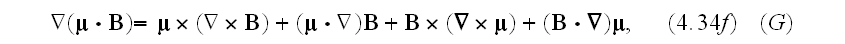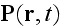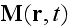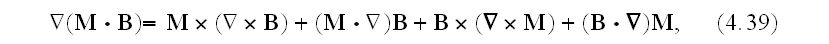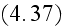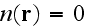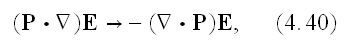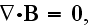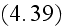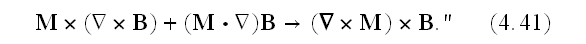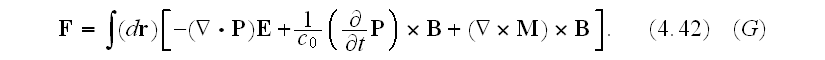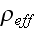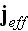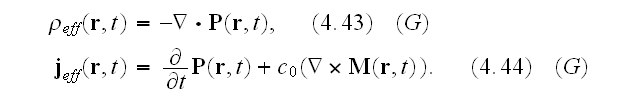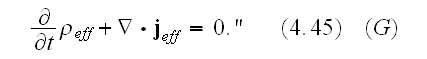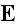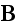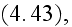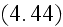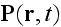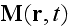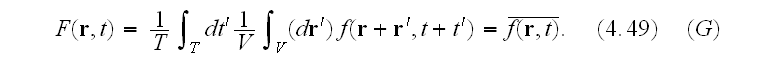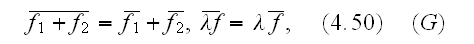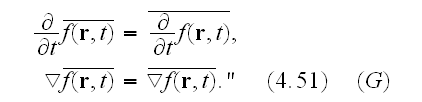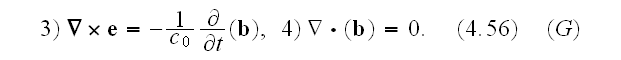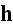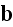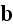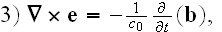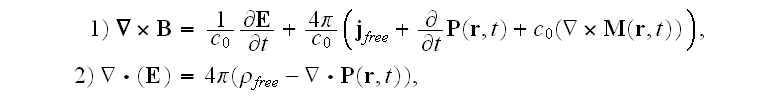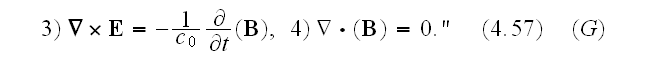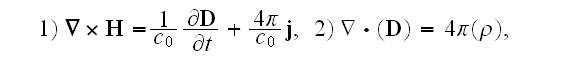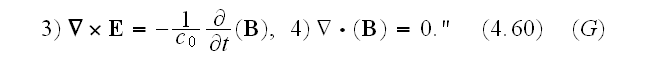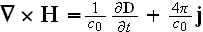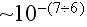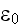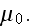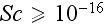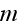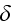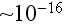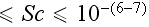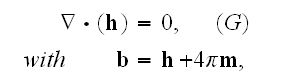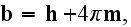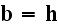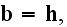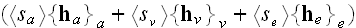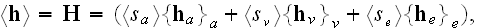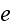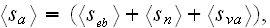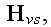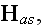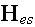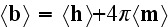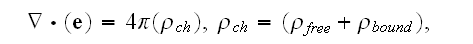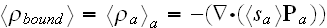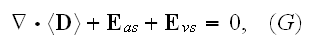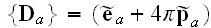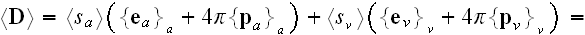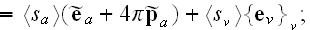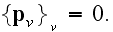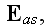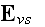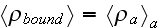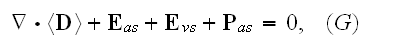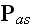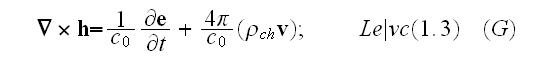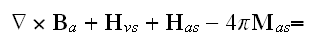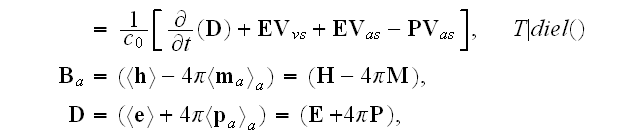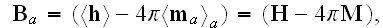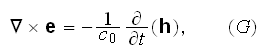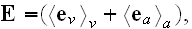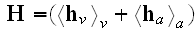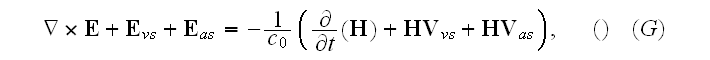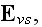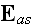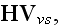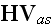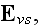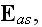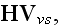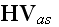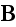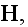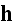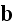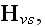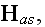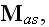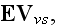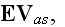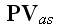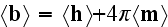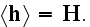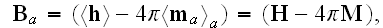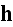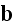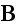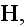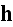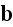The Annals of Frontier and Exploratory Science
Incompatibility of Maxwell-Heaviside-Lorentz
Electrodynamics Equations at Atomic and Continuum Scales
Vladi S. Travkin
Hierarchical Scaled Physics and Technologies (HSPT), Rheinbach, Germany,
Denver, CO, USA
Any information displayed here is the propriatary information in the area of
Incompatibility of Maxwell-Heaviside-Lorentz
Electrodynamics Equations at Atomic and Continuum Scales.
This text below and information is so far a proprietary development. Any
mentioning of the following should be strictly accompanied with the disclosure
of this website (and/or of other our sites if applicable) and the exact
context of the said information. So far it is an open information, but at any
moment can be modified or deleted.
The development concerns the incompatibility
(incompleteness) of mathematical governing equations used as the Maxwell-Heaviside-Lorentz
equations for the atomic and continuum scales electromagnetic phenomena.
The base for the statement is derived from the HSP-VAT methods that were used
to scaleport the physical and mathematical models between two (at least)
scales of phenomena depiction.
We study these phenomena in this and in closely related sub-section -
on details, logics, and modeling physical and mathematical techniques
used in the previous ~110 years sinse Lorentz found the ways to connect,
loosely communicate and justify the continuum scale Maxwell-Heaviside-Lorentz
electrodynamics equations to just discovered electron presence
in an atom, atomic scale substances, materials.
So, there was the need to develop and connect electromagnetism
phenomena and equations to those are at the atomic scale and
backward to the continuum scale for the Maxwell-Heaviside-Lorentz equations.
***********************************************
***********************************************
Introduction to Scaled Electrodynamics Description of Matter,
Materials, Substances at Scales Below Continuum - an Atomic,
Sub-atomic Ones
The main pathway of establishing the validity of Maxwell-Heaviside-Lorentz
electromagnetism modeling equations has been to prove that at any scale
(level) of description - one has the same type of model, modeling equations!
That the modeling electromagnetism equations are invariant regarding the scale
of physical phenomena considered. The only changed are the coefficients
created for that purpose.
Almost completely the talk here is about the sub-atomic and atomic scales equations (often
mentioned as microscale) and of continuum scale modeling equations.
We do not concern at this point any smaller - as of particle physics scales,
or larger as of any Heterogeneous matter, for example, astrophysics scales
electrodynamics modeling statements.
As long as it is considered as the strong true
statement in conventional homogeneous physics - that the Maxwell-Heaviside-Lorentz (MHL)
modeling electrodynamics equations are exact, precisely valid for the atomic scale phenomena,
we would accept tentatively the idea so far, that the most reliable and fundamentally
proven electromagnetism governing equations are of the atomic scale.
We have paid attention in 90s to provide the scaled description based on
correct mathematics of heterogeneous, scaled media MHL's electrodynamics phenomena
with some hard copy publications - Travkin et al. (1999a,b,c; 2000a,b; 2002),
Travkin and Catton (1999, 2001a,b,c), Travkin and Ponomarenko (2004; 2005a,b,c),
Ponomarenko et al., (2001), and other; as well as with the texts on Heterogeneous
Electrodynamics (HtEd) in this and other websites.
The very notion that at the atomic and close to this scale phenomena
in media of different plasmas are the same ideas of Scaled description
for plasma fields - as long as these fields are of particulate
substances, dominated our developments at the beginning of 2000s
regarding the Heterogeneous Scaled Electrodynamics and Momentum
Transport for plasma theory along with Continuum Mechanics that
found some presence at this website in -
The set of the Upper scale governing equations developed with HSP-VAT tools,
for those have been used the Lower scale
conventional solid state plasma modeling equations - that supposed
to be already "averaged"
- unfortunately as we point out they are not averaged -
Conventional Maxwell-Lorentz' Continuum Lower Scale Electrodynamics
and the Upper Scale Heterogeneous Electrodynamics concepts, fundamentals
obtained first in the second half of 1990s given in -
Lorentz' averaging theory type of application toward the dielectric materials fundamentals we
have shown in -
Then in other disciplines, but completely of the same origin the problems
that have been blocking advancements in considering our surrounding
matters, substances in a polyscale, polyphase nature as they are,
found some depiction in:
The important message sent by Lorentz was at the time -
1) The aether medium
was accepted as unquestionable existing phenomenon which was an inseparable
part of electrodynamics and Maxwell-Heaviside-Lorentz governing
equations.
This text by Lorentz (1906) shows definitely that Lorentz himself was totally in
agreement with experiments by D.Miller (that finally lasted for more then 30 years)
that confirmed the ether-earth drift effect while disproving the
conventionally adopted experiment by
Michelson-Morley's of 1887, which ran over only for 6 hours in four days
(see publications in the References
and other materials all over the internet).
More on that - there are studies and publications showing that the Michelson-Morley's
1887 experiment was erroneously analyzed and that the same experiment is
also in a favor of the ether-drift effect existence.
2) Maxwell had no idea (or better to say he did not recognize the outstanding Weber's
contribution into the electrodynamics field (the discussion is known and published) and
nonexistent yet atomic physics)
about electron(s), its charge, role, and all
controversy around it. But much earlier in 1840s W.Weber had, while he had developed
at that time and later the whole theory
regarding the atomic structure of matter and its relation to electrodynamics of that matter.
Many decades later at the beginning of 1900s Lorentz knew already about an electron existence
(its Weber's suggested discovery was confirmed via experiment) and
wrote the book on that published in (1906).
Lorentz' ideas and development were that
the Maxwell's equations created for unspecified "matter" that makes
transport and properties of "electricity" noticeable and meaningful,
created as of continuum medium(a) are quite suitable and for
an aether itself, and for an aether with electrons (the nucleus was not
discovered yet, but actually did not change something),
as well as for the any matter in the mathematical forms that almost
undistinguishable one from another.
3) Electrons are the volumetric, of extended size particles.
We are not discussing or assuming any invitation to argue on that now, in this
text.
However good they are, these three postulates were lately abandoned - while most of the students are
never told why? Well, to some have been told firstly the unrelated reasons.
We are turning at this point here to the multi-"phase" treatment of
atomic scale Maxwell-Heaviside-Lorentz electrodynamics equations,
as well as in few other places of this website.
Postulates Introduced in Physics During the Beginning of
Quantum Mechanics and Particle Physics Times:
1) All particles are accepted and assumed to be viewed and treated as the
"point-like," point-mass (with the mass is being Attached to this object?) or having no extended body in space.
Which was done because there
were tremendous difficulties in treatment of many-body problems in atomic
physics. There were no mathematics for that treatment and even now these
problems having approximate simulating solutions.
2) All particles and surrounding media as, for example, an air or the vacuum
were treated as the one-phase Homogeneous medium with either the space indistinguishable
locations of point-particles or with use of the Dirac's

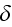 -function.
-function.
3) Because at that time there were also no concepts and theories of multi-phase
media and their methods of interaction, modeling and solution. Those were
developed much later in continuum mechanics of fluids and gases (with later on the wide applications
to other sciences and engineering) while
supported by the corresponding newly developed mathematical tools.
4) There were no boundaries, bounding surfaces for point-particles. No need to
have those. That postulate brought in the great problems.
5) So, with introduction
by Dirac the theory of electron simultaneously with the theory of

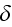 -function in 1929 there were solved two and even three tasks in atomic
physics:
-function in 1929 there were solved two and even three tasks in atomic
physics:
a) physical and mathematical fields could be continually considered
as the homogeneous ones and all powerful existing at the time mathematical mechanisms and tools for
solution of those homogeneous problems could be applied;
b) the location and
movements of particles and atoms could be assigned as for the Homogeneous fields
source functions in mathematical formulation of the tasks;
c) the powerful
methods of statistics were free to apply to the point-particles in space
behavior, advantageous for their assigned interaction collective movements and
characteristics. That was the beginning of statistical mechanics shining.
That also created the problem of near particle field's description, that
became the statistical qualities of a field.
And nobody since then is willing to explain to students - that all of this vision of particles
as point-mass particles and fields as the Homogeneous ones, was accepted in 1920s - 1930s
because they couldn't solve correctly the particulate problems as is. With particles as small,
but still physically particles and the physical fields as Polyphase, yes, of different phases
nature distributed
spatial fields. Now we can do this.
Since then, the electron and photon are the Point-mass objects with no volume and volumetric characteristics.
Since then, the huge body of mathematics, let alone physics, has been developed just to support this
artificial picture. While physics became a metaphysical science, because of false point-particles, MHL electrodynamics,
SR and GR following from this short-hand electrodynamics, and QM that became the compounding original theory
for everything small enough to not study it within.
6) With these above assumptions (1-4) that was not surprising that Quantum Mechanics was introduced
and advanced
in this fantastic mathematical formulation as we know it now. Little later Dirac's

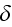 -function added greatly to the functionality of the hard solid rock of QM that is laying on
the road to further progress in physics for many decades.
-function added greatly to the functionality of the hard solid rock of QM that is laying on
the road to further progress in physics for many decades.
These words above is not the critics of QM, the critics is in the other places of this website. Also, people
started to find inconsistencies, flaws in QM in the earlier years of QM appearance. And that was not too hard.
Unfortunately, QM is being taught to students and used for research up to now as the primary theory
for micro-world, sub-atomic physics.
Teachers do not tell that QM is just one of the approximate theories that
was developed due to
insolvency of mathematics and physics regarding mentioned issues at that time.
But not at present situation, when those statements of 1920-1930s can be solved,
because the theories for that solution during the last 20-30 years have been advanced far enough.
Maxwell's Ideas of Electromagnetism and Governing
Mathematical Equations
Maxwell (2002a; 3rd ed.) in introductory paragraphs
admitted the level of contemporary to his time knowledge of electromagnetism
(electricity) phenomena.
In p. 37 one can read that:
"When we come to describe electrometers and multipliers we shall find that
there are still more delicate methods of detecting electrification and of
testing the accuracy of our theorems, but at present we shall suppose the
testing to be made by connecting the hollow vessel with a gold leaf
electroscope. This method was used by Faraday in his very admirable
demonstration of the laws of electrical phenomena."
Our comments:
Maxwell straight in denoting that he uses few theorems for explanation of
electromagnetic phenomena. Gauss-Ostrogradsky theorem was among of them.
In p. 38 one can read:
"35. While admitting electricity, as we have now done, to the rank of a
physical quantity, we must not too hastily assume that it is, or is not, a
substance, or that it is, or is not, a form of energy, or that it belongs to
any known category of physical quantities. All that we have hitherto proved is
that it cannot be created or annihilated, so that if the total quantity of
electricity within a closed surface is increased or diminished, the increase
or diminution must have passed in or out through the closed surface.
This is true of matter, and is expressed by the equation known as the Equation
of Continuity in Hydrodynamics.
It is not true of heat, for heat may be increased or diminished within a
closed surface, without passing in or out through the surface, by the
transformation of some other form of energy into heat, or of heat into some
other form of energy."
In p. 39 one can read:
"There is, however, another
reason which warrants us in asserting that electricity, as a
physical quantity, synonymous with the total electrification of a
body, is not, like heat, a form of energy. An electrified
system has a certain amount or energy, and this energy can be calculated by
multiplying the quantity of electricity in each of its parts by another
physical quantity, called the Potential, of that part, and taking half the sum
of the products. The quantities 'Electricity ' and 'Potential,' when
multiplied together, produce the quantity 'Energy.' It is impossible,
therefore, that electricity and energy should be quantities of the same
category, for electricity is only one of the factors of energy, the
other factor being 'Potential.'"
Our comments:
Maxwell is vague about connection "electricity" with energy.
In p. 40 one can read:
"In the theory called
that of Two Fluids, all bodies, in their un-electrified state, are
supposed to be charged with equal quantities of positive and negative
electricity. These quantities are supposed to be so great that no process of
electrification has ever yet deprived a body of all the electricity of either
kind. The process of electrification, according to this theory, consists in
taking a certain quantity P of positive electricity from the body A and
communicating it to B, or in taking a quantity N of negative electricity from
B and communicating it to A, or in some combination or these processes.
The result will be that A will have P+N units of negative electricity over and
above its remaining positive electricity, which is supposed to be in a state
of combination with an equal quantity of negative electricity. This quantity
P+N is called the Free electricity, the rest is called the Combined, Latent,
or Fixed electricity."
"We shall see that the
mathematical treatment of the subject has been greatly developed by writers
who express themselves in terms of the 'Two Fluids' theory. Their results,
however, have been deduced entirely from data which can be proved by
experiment, and which must therefore be true, whether we adopt the theory of
two fluids or not. The experimental verification of the mathematical results
therefore is no evidence for or against the peculiar doctrines of this theory.
The introduction of two fluids permits us to consider the negative
electrification of A and the positive electrification of B as the effect of
any one of three different processes which would lead to the same result. "
"37. In the theory of One Fluid everything is the same as in
the theory of Two Fluids except that, instead of supposing the two substances
equal and opposite in all respects, one of them, generally the negative one,
has been endowed with the properties and name of Ordinary Matter, while the
other retains the name of The Electric Fluid. The particles of the
fluid are supposed to repel one another according to the law of the
inverse square of the distance, and to attract those of matter according to
the same law. Those of matter are supposed to repel each other and attract
those of electricity."
"This theory does not, like the
Two-Field theory, explain too much. It requires us, however, to suppose the
mass of the electric fluid so small that no attainable positive or negative
electrification has yet perceptibly increased or diminished either the mass or
the weight of a body, and it has not yet been able to assign sufficient
reasons why the vitreous rather than the resinous electrification should be
supposed due to an excess of electricity."
In p. 43 Maxwell summarizing his
intent in the manuscript:
"In the present treatise I propose, at different stages of the investigation,
to test the different theories in the light of additional classes of
phenomena. For my own part, I look for additional light on the nature of
electricity from a study of what takes place in the space intervening between
the electrified bodies. Such is the essential character of the mode of
investigation pursued by Faraday in his Experimental Researches, and as we go
on I intend to exhibit the results, as developed by Faraday, W. Thomson,
&c., in a connected and mathematical form, so that we may perceive what
phenomena are explained equally well by all the theories, and what phenomena
indicate the peculiar difficulties of each theory."
Our comments:
We need to understand that Maxwell saw the nature of electromagnetic
phenomena as a kind of ones happening in and with participation of aether
and by some unknown at that time (to all seems, but W.Weber and some collaborators) "portions of matter"
that he forecasted would give a possibility to construct the matter
related "dynamical theory of electricity" - see
in our CONCLUSIONS citations on that.
While he was not sure (he disputed Weber's electrodynamics) at the time of what kind of media
provides for electromagnetic
phenomena - even could be a fluid like.
Wilhelm Weber, Carl Friedrich Gauss and Continental School of Thought Accomplishments
Regarding Electromagnetism Phenomena, Electrodynamics and even
Atomic Physics
In the review by Hecht (2001) we might read that:
"It is not too difficult to see that Weber's Fundamental Electrical Law,
almost unknown today, is a statement of a relativistic law of physics,
long predating the statement of relativity we are accustomed to^8.
Here it is the force, rather than the mass, which varies with the relative motion.
But, not only does it predate the Einstein formulation, it is methodologically
far superior. One can, in various ways, attempt to show an equivalence of the
two statements, but the usefulness of such efforts is doubtful. The problem lies
elsewhere. The two statements lie in two entirely different domains.
One is a continuation of the Leibnizian current of physics; the other,
whatever the intentions,
serves to hide errors embedded in the assumptions
underlying the Maxwell equations. "
Our comments:
Yes, this author had been brave enough to publish the statement on inadequacy of
Maxwell-Heaviside-Lorentz electrodynamics. And only well organized political support
has been preventing the issue from studying, from the ground and up systematic research, and
improvement or advancement.
We have obtained the theory for collective (averaged) action of the Weber's and other known force interaction between the charged particles
formulae suggested by J.Klyushin first for the two-particles interaction. This theory by Klyushin
actually embraced the whole set of others well grounded fundamental interactions (including of Weber's)
between the two
charged particles that are still, as in the Coulomb formula, and/or are in motion
and well known today. The parts of this theory are placed in this and other our sites,
in hard copy publications, and will be disseminated to more applications.
We will be exploring this and many other notices, and works to go in that same
developmental direction regarding the Ampère-Gauss-Weber, others electrodynamics base and features
as that includes at least the two physical spatial scale physical
models and
what are making them if all that to be taken combined for the closed in some aspects the strictly
connected and scaleported physical system effected and controlled by its external input
either from Upper or at the Lower scale spatial and temporal boundaries.
We will be adding to this part of historical observations regarding
the electrodynamics of continental school of thought - Ampère-Gauss-Weber,
and contemporary electrodynamics working scientists, that are actually support our current
time (1987 - 2010s) electrodynamics Polyphase-Polyscale-Polyphysics (3P) theory.
The theory that is of scaled base from the
sub-atomic particles while induces
the laws of electrical particles interaction. Structural particles - not a point-mass ones.
Lorentz formulated Electrodynamics Governing Equations
for the Ether, Ether and Electrons Medium, and for a Matter,
Material of Continuum Mechanics
Lorentz (1906, 1952) in his lectures of 1906, when the discovery of electron
had already impacted the physics world, gives the following sets of equations
for an ether, for the quantity of electrons in an ether, and for a bulk
formulated continuum mechanics material.
Lorentz in the "The Theory of Electrons and Its Applications
to the Phenomena of Light and Radiant Heat : a Course of Lectures Delivered in
Columbia University in 1906" (1906) writes in page 5: (
equations in an aether) -
"3. We are now prepared to write down the fundamentals
equations for the electromagnetic field in the form which they take for the
ether. We shall denote by

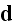 the electric force, the same symbol serving for the dielectric displacement,
because in the ether this has the same direction and, on account of the choice
of our units, the same numerical magnitude as the electric force. We shall
further represent by
the electric force, the same symbol serving for the dielectric displacement,
because in the ether this has the same direction and, on account of the choice
of our units, the same numerical magnitude as the electric force. We shall
further represent by

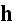 the magnetic force and by
the magnetic force and by

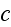 a constant depending on the properties of the ether.
a constant depending on the properties of the ether.
A third vector is the current

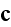 ,
which now consists only of the displacement
current of Maxwell. It exists wherever the dielectric displacement
,
which now consists only of the displacement
current of Maxwell. It exists wherever the dielectric displacement

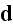 is
a function of the time, and is given by the formula
is
a function of the time, and is given by the formula
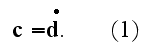
In the form of differential equations, the formulae of the electromagnetic
field may now be written as follows:
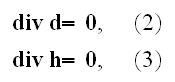
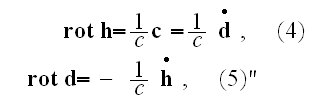
here

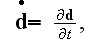

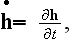 used as a partial derivative with respect to the time.
used as a partial derivative with respect to the time.
Our comments:
Note that only two functions used here

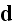 and
and

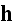 ,
where in an ether (or "vacuum") the
displacement
,
where in an ether (or "vacuum") the
displacement
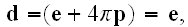 because the electric dipole
moment
because the electric dipole
moment
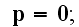 and where
and where

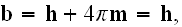 because magnetic dipole moment is
because magnetic dipole moment is

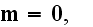
Note that the

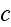 in Lorentz's physical statement is the "constant depending on the
properties..."
in Lorentz's physical statement is the "constant depending on the
properties..."
But not a light speed or something as that kind.
Further in this page Lorentz explains the equations:
"The third equation, conjointly with the second, determines the magnetic field
that is produced by a given distribution of the current

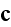 .
As to the last equation, it expresses the law according to which electric
forces are called into play in a system with a variable magnetic field, i.e.
the law of what is ordinary called electromagnetic induction. The formulae (),
() and (5) are vector equations and may each be replaced by three scalar
equations relating to the separate axes of coordinates."
.
As to the last equation, it expresses the law according to which electric
forces are called into play in a system with a variable magnetic field, i.e.
the law of what is ordinary called electromagnetic induction. The formulae (),
() and (5) are vector equations and may each be replaced by three scalar
equations relating to the separate axes of coordinates."
Lorentz writes interesting things about electromagnetism in
an ether, p. 6:
"The formulae for the ether constitute the part of electromagnetic
theory that is most firmly established. Though
perhaps the way in which they are deduced will be changed in future
years, it is hardly conceivable that the equations themselves will have
to be altered. "
Now we write the Lorentz' electrodynamics equations for a volume in an
aether with number of electrons - p. 11-12:
"7. I have now to make you acquainted with the equations
forming the foundation of the mathematical theory of electrons. Permit me to
introduce them by some preliminary remarks.
In the first place, we shall ascribe to each electron certain
finite dimensions, however small they may be, and we shall fix our
attention not only on the exterior field, but also on the interior space, in
which there is room for many elements of volume and in which the state of
things may vary from one point to another.
As to this state, we shall suppose it to be of the same kind as at outside
points. Indeed, one of the most important of our fundamental assumptions must
be that the ether not only occupies all space between
molecules, atoms or electrons, but that it pervades all these
particles.
We shall add the hypothesis that, though the particles may
move, the ether always remains at rest.
We can reconcile ourselves with this, at first sight, somewhat startling idea,
by thinking of the particles of matter ad of some local modifications in the
state of the ether. These modifications may of course very well travel onward
while the volume-elements of the medium in which they exist remain at rest.
Now, if within an electron there is ether, there can also be an
electromagnetic field, and all we have got to do is to
establish a system of equations that may be applied as well to the parts of
the ether where there is an electric charge, i.e. to the electrons, as to
those where there is none. As to the distribution of the charge, we are
free to make any assumption we like.
For the sake of convenience we shall suppose it to be distributed over
a certain space, say over the whole volume occupied by the electron, and we
shall consider the volume-density

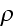 as
a continuous function of the coordinates, so that the charged particle has no
sharp boundary, but is surrounded by a thin layer in which the
density gradually sinks from the value it has within the electron to 0.
as
a continuous function of the coordinates, so that the charged particle has no
sharp boundary, but is surrounded by a thin layer in which the
density gradually sinks from the value it has within the electron to 0.
Thanks to this hypothesis of the continuity of

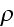 ,
which we have never to trouble ourselves about surfaces of discontinuity, nor
to encumber the theory by separate equations relating to these.
,
which we have never to trouble ourselves about surfaces of discontinuity, nor
to encumber the theory by separate equations relating to these.
Morever, if we suppose the difference between the ether within and without the
electrons to be caused, at least so far as we are concerned with it, only by
the existence of the volume-density in the interior, the equations for the
external field must be got from those for the internal one by simply putting

 so that we have only to write down one system of differential equations.
so that we have only to write down one system of differential equations.
Of course, these must be obtained by a suitable modification, in which the
influence of the charge is expressed, of the equations (2)-(5) which we have
established for the free, i.e. for the uncharged ether. It has been found that
we can attain our object by the slightest modification imaginable, and that we
can assume the following system
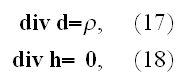
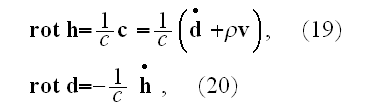
in which the first and the third formula are the only ones that have been
altered.
In order to justify these modifications, I must in the first place recall to
your minds the general relation existing in Maxwell's theory between the
dielectric displacement across a closed surface and the amount of charge

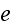 contained within it. It is expressed by the
equation
contained within it. It is expressed by the
equation
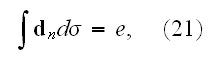
in which the integral relates to the closed surface.... "
Here in (19)
"
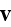 is the velocity of the charge".
is the velocity of the charge".
Our comments:
Contrary to Lorentz' simplified assumption that allowed him to write the same
kind of equations with the space-dependable Lower scale homogeneous equations
governing the electromagnetic fields, we would use the
"phase"-dependable media interacting within our region with particles
- just some of the kinds, and the "vacuum" which is in reality not
the vacuum at the lower scales physics.
These equations (17)-(20) are supposed to be the averaged equations - for the
aether and plus electrons as a total mixed medium! Because there is less
understanding and function performed due to mutual dependencies by these
equations, the equations responsible for the volumetrically mutual interactive
actions, but not for dimensionless point interface when the fields determined
by space-dependable functions as

 and
and

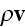 -
unless we consider the collective, averaged fields in an area.
-
unless we consider the collective, averaged fields in an area.
That means these equations (17)-(20) in the scalable notations should be
written for averaging as
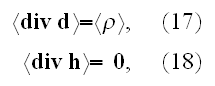
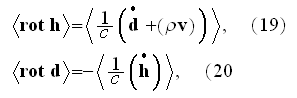
and these equations if averaged correctly are not the ones written in
textbooks as (in other dimensions systems as SI looking slightly different)
the following
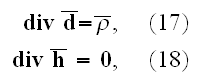
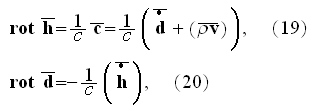
**************
Well, the EM equations by Lorentz (1906) in a matter are (p.
7):
"4. There is one way of treating these phenomena that is
comparatively safe and, for many purposes, very satisfactory. In following it,
we simply start from certain relations that may be considered as expressing,
in a condensed form, the more important results of electromagnetic
experiments. We have now to fix our attention on four vectors, the electric
force

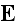 ,
the magnetic force
,
the magnetic force

 ,
the current of electricity
,
the current of electricity

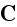 and
the magnetic induction
and
the magnetic induction

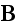 .
These are connected by the following fundamental equations:
.
These are connected by the following fundamental equations:
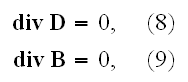
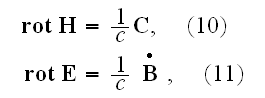
presenting the same form as the formulae we have
used for the ether.
In the present case however, we have to add the relation between

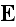 and
and

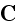 on
the one hand, and that between
on
the one hand, and that between

 and
and

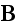 on
the other. Confining ourselves to isotropic bodies, we can often describe the
phenomena with sufficient accuracy by writing for the dielectric displacement
on
the other. Confining ourselves to isotropic bodies, we can often describe the
phenomena with sufficient accuracy by writing for the dielectric displacement
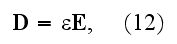
a vector equation which expresses that the displacement has the same direction
as the electric force and is proportional to it. The current in this case is
again Maxwell's displacement current
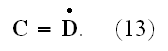
In conducting bodies on the other hand, we have to do with a current of
conduction, given by
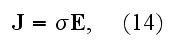
where

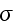 is
a new constant. This vector is the only current and therefore identical to
what we have called
is
a new constant. This vector is the only current and therefore identical to
what we have called

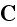 ,
if the body has only the properties of a conductor. In some cases however, one
has been led to consider bodies endowed with the properties of bothconductors
and dielectrics.
,
if the body has only the properties of a conductor. In some cases however, one
has been led to consider bodies endowed with the properties of bothconductors
and dielectrics.
If, in a substance of this kind, an electric force is supposed to produce a
dielectric displacement as well as a current of conduction, we may apply at
the same time (12) and (14), writing for the total current
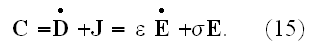
Finally, the simplest assumption we can make as to the relation between the
magnetic force and the magnetic induction is expressed by the formula
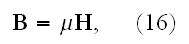
in which

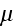 is a new constant. "
is a new constant. "
Our comments:
Note here, that there were no averaging operators at all by the Lorentz time.
There were no atomic physics as a discipline and the nucleus will be
discovered only in 1911.
So, the mathematical formulation of the continuum electrodynamics were found
based on general considerations of experiments and with the homogeneous
Volume-Surface theorems by mostly as the Gauss-Ostrogradsky and Green's
theorems.
But not with any kind of averaging techniques at atomic scale used for
Maxwell-Lorentz equations.
In p. 8 further Lorentz gives few outstanding sentences
regarding the role of modeling in electromagnetism:
"If we want to understand the way in which electric and magnetic properties
depend on the temperature, the density, the chemical constitution or the
crystalline state of substances, we cannot be satisfied with simply
introducing for each substance these coefficients, whose values are to be
determined by experiment; we shall be obliged to have recourse to some
hypothesis about the mechanism that is at the bottom of the phenomena."
In pgs. 8-9 Lorentz writes:
"In a ponderable dielectric there can likewise be a motion of the electrons.
Indeed, though we shall think of each of them as having a definite position of
equilibrium, we shall not suppose them to be wholly immovable. They can be
displaced by an electric force exerted by the ether,
which we conceive to penetrate all ponderable matter, a point to which we
shall soon have to revert."
Our comments:
Lorentz straightly supports here the ether as the
medium for transduction of electromagnetic phenomena!
In p. 9 Lorentz continues:
"Now, however, the displacement will immediately give rise to a new force by
which the particle is pulled back towards its original position, and which we
may therefore appropriately distinguish by the name of
elastic force.
The motion of the electrons in non-conducting bodies, such as glass and
sulphur, kept by the elastic force within certain bounds, together with the
change of the dielectric displacement in the ether itself, now constitutes
what Maxwell called the displacement current. A substance in which the
electrons are shifted to new positions is said to be electrically polarized.
Again, under the influence of the elastic forces, the
electrons can vibrate about their positions of
equilibrium. In doing so, and perhaps also on account of other more irregular
motions, they become the centers of waves that travel
outwards in the surrounding ether and can be observed as light if the
frequency is high enough. In this manner we can account for
the emission of light and heat."
Our comments:
Note here - that there is no mentioning of photons. Photons were just suggested recently,
still did not come into the system of Lorentz's physical world, probably.
The light is explained in this text as through the "surrounding ether and can be observed
as light" in a vibrating ether!
What kind of averaging theory Lorentz developed and applied toward
the dielectric materials fundamentals we have shown in -
Note, that these incorrect for heterogeneous, polyscale media
averaging procedures dominated the first half of XX century.
Atomic Scale (Microscale) Maxwell-Heaviside-Lorentz Equations
(with Partial Time Derivatives) and
Their Fields and Media in SI and CGSE Systems
Lorentz

 style
of EM equations in the vacuo for SI system
style
of EM equations in the vacuo for SI system
Finally we can arrive to the
Lorentz
 style of EM equations in the vacuo for SI system (as
the vacuum we will use the medium as it is the
"vacuum", at least consisting as of one of its componets the
cosmic relict radiation field -- Cosmic Microwave Background (CMB) radiation
and more on that. With
style of EM equations in the vacuo for SI system (as
the vacuum we will use the medium as it is the
"vacuum", at least consisting as of one of its componets the
cosmic relict radiation field -- Cosmic Microwave Background (CMB) radiation
and more on that. With

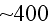 photons of it in each
photons of it in each

![$[cm^{3}]$](/eldyn/incompat/IncompatMaxwell206__55.gif) and with the influx of those photons as of
and with the influx of those photons as of

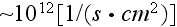 ) when
) when

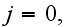

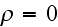 of
course
of
course

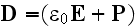 or for vacuum
or for vacuum

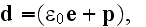 while
medium can be taken as polarization free
while
medium can be taken as polarization free

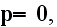
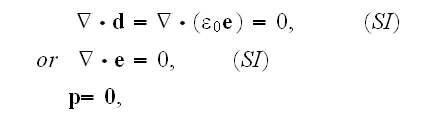

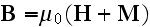 or for vacuum
or for vacuum

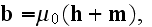 while medium can be taken as magnetization free
while medium can be taken as magnetization free

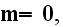
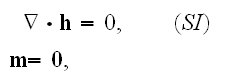
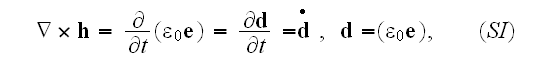
from

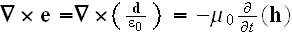
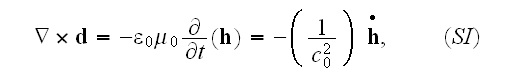
*********************************************************************
Now the set of Maxwell GE in SI
with

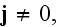

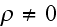 for vacuum and
for vacuum and

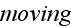

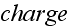 point-like
point-like

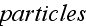 as
for
as
for

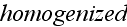

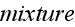 when
when


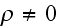 :
:
Gauss' law equation

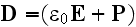 or for vacuum
or for vacuum

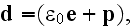 but with
but with

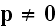 only AFTER like averaging. So, before averaging we need to
take
only AFTER like averaging. So, before averaging we need to
take

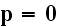 .
Well, so far following the methods to connect atomic scale electromagnetism
and macroscale Maxwell-Lorentz equations we do take
.
Well, so far following the methods to connect atomic scale electromagnetism
and macroscale Maxwell-Lorentz equations we do take

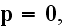 and
and

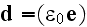 .
.

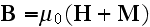 or for vacuum
or for vacuum

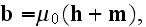 while also with
while also with

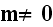 only AFTER like averaging.
only AFTER like averaging.
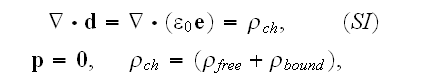
where in the Lorentz' form for


 properties
fields we have
properties
fields we have
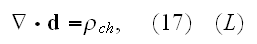
conservation
of magnetic flux equation
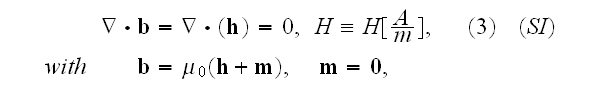
where

 means
means

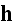 for vacuum conditions, while the Lorentz' equation is
for vacuum conditions, while the Lorentz' equation is
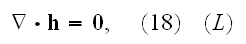
Maxwell's-Ampere's law equation: at the macroscales
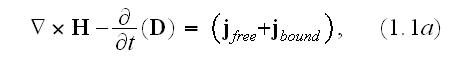
or it can be re-written as to go closer to of the Lorentz's equation when

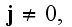 because
because

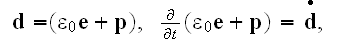 before
averaging
before
averaging 
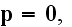 and
and

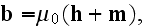 with
with

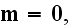 and
and

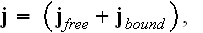 finally
finally
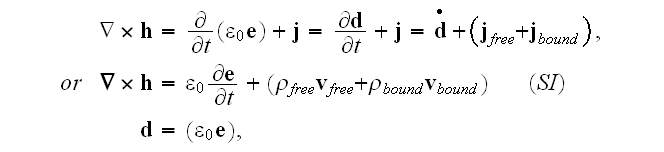
well, but in textbooks authors like or see advantages in presenting this
equation via the microscale magnetic
induction
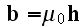 field. Why is that? Apparently because - in this way or reasoning they do the jump
straight to the macroscale magnetic
induction
field. Why is that? Apparently because - in this way or reasoning they do the jump
straight to the macroscale magnetic
induction
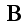 ,
as does Jackson (1999) in eq. (6.64), where already at the microscale appeared
magnetic
induction
,
as does Jackson (1999) in eq. (6.64), where already at the microscale appeared
magnetic
induction
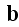 (the following is the Maxwell's-Ampere's law equation from the set of
microscopic equations for electromagnetism in (6.64) in Jackson (1999) )
(the following is the Maxwell's-Ampere's law equation from the set of
microscopic equations for electromagnetism in (6.64) in Jackson (1999) )
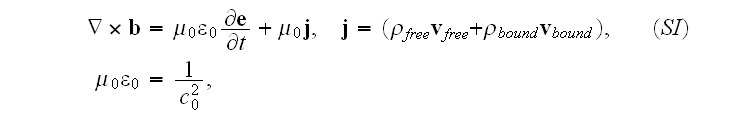
while Lorentz in his system
with 
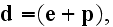

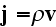 got to
got to
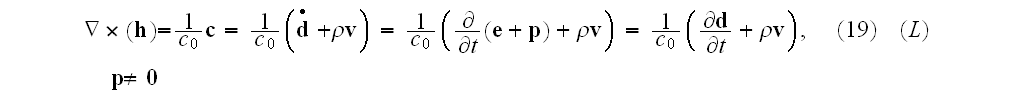
Faraday's law of induction equation
for vacuum with homogenized particles

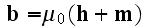 and we are able to take in the right hand side as
and we are able to take in the right hand side as

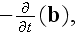 as it looks like reasonable.
as it looks like reasonable.
*******
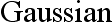 system
in the vacuum with
system
in the vacuum with

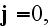

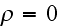 **********************
**********************
Now in

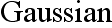 system
of variables this set of Lorentz' style GE of Jackson
for "active" vacuum will be as (following (with
system
of variables this set of Lorentz' style GE of Jackson
for "active" vacuum will be as (following (with

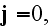

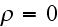 )
)

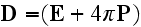 or for vacuum
or for vacuum

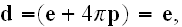

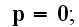

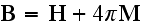 or for vacuum
or for vacuum

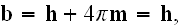

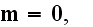
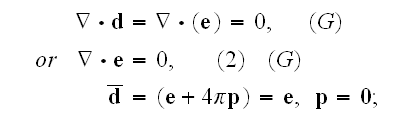
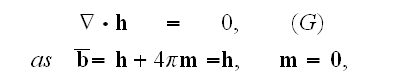
in "active"vacuum
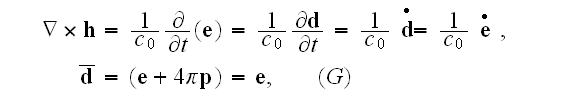
while

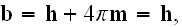

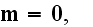

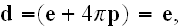

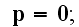
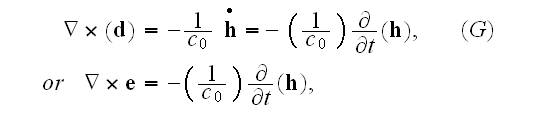
well, these GE exactly as eqs. (2)-(5) in p. 5 in Lorentz
(1906, 1952).
****************************************************
Now the set of equations in the Gaussian system (CGSE) for a substance

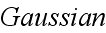

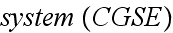
with

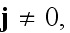

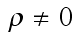
of variables for vacuum and

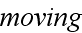
point-like

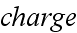

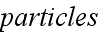 as
for
as
for

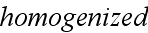

when

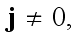

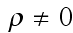 :
:
Gauss' law equation

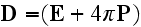 or for vacuum with charges-particles
or for vacuum with charges-particles

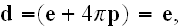

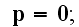

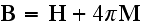 or for vacuum
or for vacuum

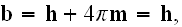

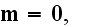
before averaging
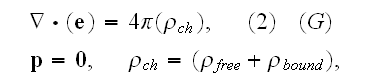
where in the Lorentz' form for the



 we have
we have
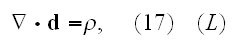
the next one is the conservation of magnetic flux equation or
Gauss law for magnetic field equation which is before averaging
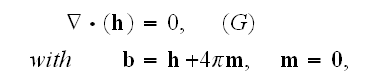
where

 means
means

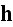 for vacuum conditions, while the Lorentz' equation is
for vacuum conditions, while the Lorentz' equation is
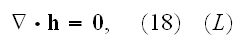
Maxwell's-Ampere's law equation
before averaging
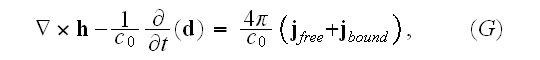
or it can be re-written as to go closer to one of the Lorentz's equation when

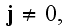 because for vacuum with separately included and not averaged charges-particles would be
because for vacuum with separately included and not averaged charges-particles would be

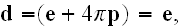

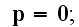
for vacuum

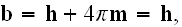

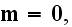

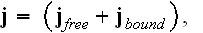 finally
finally
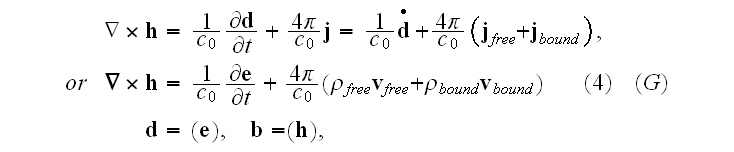
well, but in textbooks authors like or see advantages in presenting this
equation via the microscale magnetic
induction
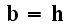 field. Why is that? I know why - in this way or reasoning they do jump
straight to the macroscale magnetic
induction
field. Why is that? I know why - in this way or reasoning they do jump
straight to the macroscale magnetic
induction
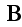 ,
as does Jackson (1999) in eq. (6.64), where already at the microscale appeared
magnetic
induction
,
as does Jackson (1999) in eq. (6.64), where already at the microscale appeared
magnetic
induction
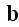
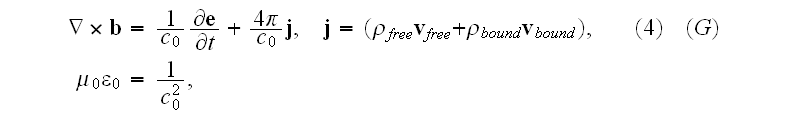
for vacuum with charges-particles

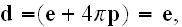

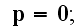
for vacuum

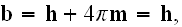

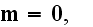
while Lorentz in his system
with 
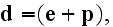

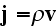 got to
got to
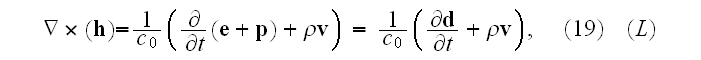
Faraday's law of induction equation
before averaging
If we take the full form of constitutive equations for system of vacuum plus
the charges

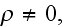

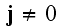 with
with

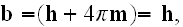

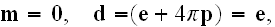

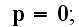

 we
would have
we
would have
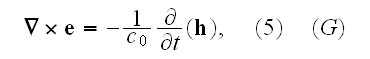
or (also before Averaging)
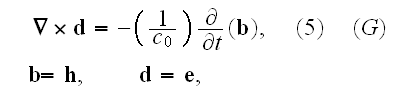
the same as of Lorentz (1906, 1959).
Schwinger et al. (1998) Pseudo-Averaging Techniques for
Unspecified Volume Atomic Scale Fields
In the textbook by Schwinger et al. (1998) given the good example of
reasoning, methods used in homogeneous physics to derive (and by this
to validate, justify) the Maxwell-Heaviside-Lorentz electrodynamics equations
for a continuum. Everyone was able to analyze these rather complicated
mathematically ideas and methods used for "homogenized" mixing of atomic
scale particles and of the "vacuum" to get Up to the continuum media
electromagnetism governing equations.
We would extend our consideration of this theory in attempts to
contribute for the multi"phase" Scaleportation of electrodynamics
equations, models between atomic and continuum descriptions.
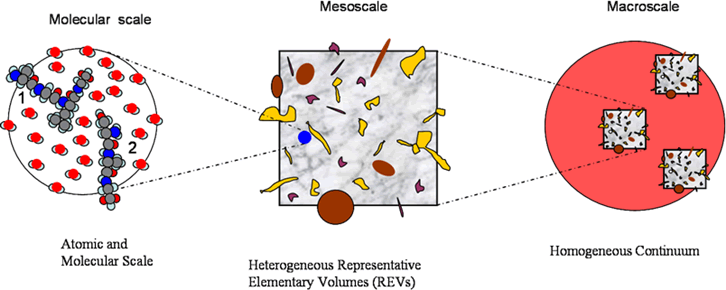
Figure 1: Simplified drawing
of the Bottom-Up
consecutive series of Representative
Elementary Volumes (REVs) at three scales from a molecular to continuum one:
1st polypeptide -- alanine-glycine-valine-glycine;
2nd -- serine-alanine-glycine in solvent of water.
Also we leave here for comparison, and for interest, in this figure
the WRONG IMAGES for water molecules -
as the unstructured 3 circles known in COHP. Comparison see in Figure 4.
Note, that the molecules and phases
are free to "flow" throughout
or stay at the Bounding REV Surfaces. While this is explicitly prohibited
while doing Homogeneous Averaging, isn't?
In Homogeneous physics - like in the tested below monograph by
Schwinger et al. (1998) and others, there are no specifics, theorems to
do averaging over these REVs, and even there are no definitions or wrong definitions
(as in Continuum Homogeneous Mechanics) of a REV.
In p. 33 one can read that:
"4.1 Force on an Atom
"The Maxwell-Heaviside-Lorentz system of equations, (1.65) and (1.68), provides a
microscopic description of electromagnetic phenomena, at the classical level,
ranging from the simplest two-particle system to the detailed behavior of all
particles in a macroscopic system.
However, for the latter case, we usually do not require such a complete
description, since our measurements involve macroscopic quantities which are
only indirectly related to the microscopic behavior of individual atoms.
We must develop a theory that is directly
applicable to the macroscopic situation with only an implicit reference back
to the detailed characterization of the system."
Our comments:
These authors did not believe in the possibility of true scaleportation -
purely because of the lack of their knowledge, partially the reasons were about the
HSP-VAT tools and advancements up to that time - the mid-90s.
At the same time, it is obvious that very established in traditional Homogeneous
physics authors would not be so naive to break with the ground base concepts of
absence of Heterogeneous
instruments in Atomic physics as it was continued for the 90-something years.
Also it is true that this book with the so straight interest and methods
to justify the conventional homogeneous derivation procedures, mathematics
used for "averaging" in Atomic physics serving to the needs in orthodox physics
for justification of that sort of thinking and the status quo - as for a homogeneous matter
even when the tools
and the solid base exist for treating heterogeneous microscale electrodynamics phenomena
with the heterogeneous physics and math tools.
Further down the p. 33:
"The resulting macroscopic electrodynamics is a phenomenological theory, by
which is meant a theory that operates at the level of the phenomena being
correlated and predicted, while maintaining the possibility of contact with a
more fundamental theory - here, microscopic electrodynamics - that
operates at a deeper level."
Our comments:
What an egocentric declaration - the results of statistical operations
over the point-objects of
conventional atomic physics are taken as of higher superiority over the exact
analytical methods and procedures for modeling and simulation of relevant
scaled problems.
This kind of up and down points of view regarding the statistical physics and
deterministic physics cooperation registered for existing since the XVIII. It is
not new completely.
Further down the p. 33-34:
"That contact exists to the extent that the
macroscopic measurements can be
considered to be averages, over very many atoms, of the results of
hypothetical microscopic measurements.
To begin, we consider an atom, an electrically neutral assembly of
point charges (outlined by us),
that are bound in a small region. We want to study the response of such a
system to external electric and magnetic fields that vary only slightly over
the spatial extent of that system.
We will first concentrate our attention on the net force on the system at a
given time, the sum of the forces on its constituents, (1.68), (force law by
Lorentz, H.A.)
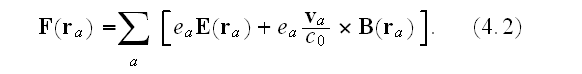
Since the system is small, all the charges are near the center of mass of the
charge distribution, which lies at the position

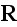 .
(For the purposes of the following expansion we could let
.
(For the purposes of the following expansion we could let

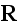 represent
an arbitrary point inside the charge distribution; the use of the center of
mass allows us to separate intrinsic properties from those due to the motion
of the atom as a whole.)
represent
an arbitrary point inside the charge distribution; the use of the center of
mass allows us to separate intrinsic properties from those due to the motion
of the atom as a whole.)
We can then expand the electric and magnetic fields about this reference
point,
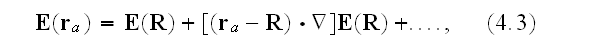
and like wise for

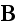 ,
in which the subsequent terms are considered negligible."
,
in which the subsequent terms are considered negligible."
Our comments:
Well, this is the expansion named the one that is up to the first order of
variable's (function usually) magnitude. And considered in mathematics of
lower order of accuracy.
In physics it is often, especially in complicated areas, taken as the final
and most often used tool to get to some results out of despair in search for
any kind of solution.
Here we talk on that because students in physics and techs usually can not
assess the motifs for this or that direction in taught material.
Further down the p. 34:
"Here

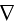 means the gradient with respect to . Now, the total force on the atom,
(4.2), can be rewritten in terms of this expansion
as
means the gradient with respect to . Now, the total force on the atom,
(4.2), can be rewritten in terms of this expansion
as

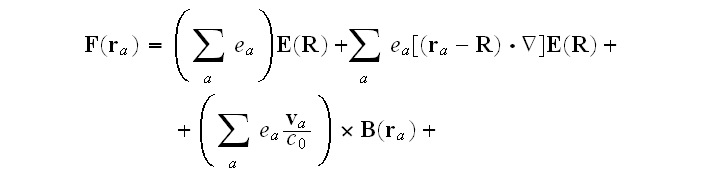
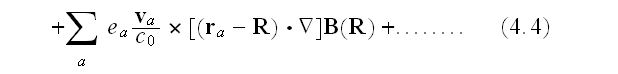
In p. 38 one can read that:
"4.2 Force on a Macroscopic Body
..... Macroscopic materials are made up of large numbers of atoms. What is
the total force on such a piece of materials? We must sum up all the forces on
the individual atoms. To the extent that the forces on the atoms vary but
slightly from one atom to another, the simulation can be replaced by a volume
integration, weighted by the atomic density,

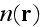 ,
the number of atoms per unit volume at the macroscopic point
,
the number of atoms per unit volume at the macroscopic point

 :
:
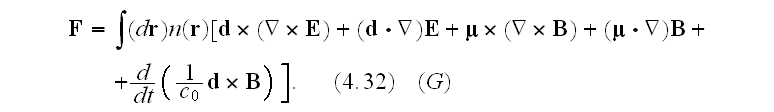
Notice that we have rewritten (4.22) with the aid of the identities
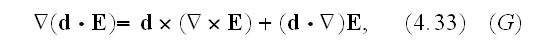
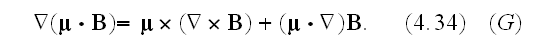
First a word about

 and
and

 in
these expressions. In the single atom formula (4.22), the derivatives act only
on
in
these expressions. In the single atom formula (4.22), the derivatives act only
on

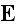 and
and

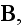 which is reflected in (4.32). For a many-atom system, the dipole moments could
well vary from one location to another and so have macroscopic spatial
dependence. Accordingly,
which is reflected in (4.32). For a many-atom system, the dipole moments could
well vary from one location to another and so have macroscopic spatial
dependence. Accordingly,

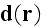 and
and

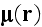 are
the average dipole moments at the point
are
the average dipole moments at the point

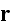 .
.
We now define the electric polarization,

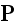 ,
and the magnetization,
,
and the magnetization,

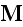 ,
by
,
by
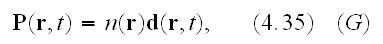
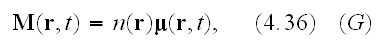
respectively. The resulting macroscopic form of the total force at time

 is
is
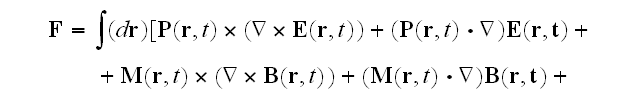
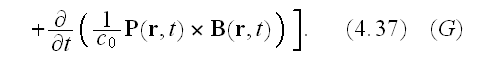
(Here the distinction between

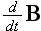 and
and

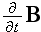 has
been dropped, because the "
has
been dropped, because the "
Our comments:
The identities (4.33), (4.34) are not complete expressions.
Those should look like (4.33f), (4.34f)
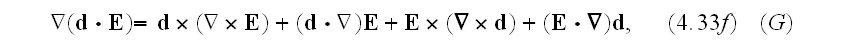
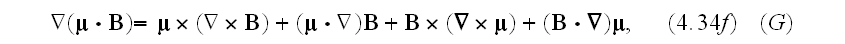
that is the difference.
Also, authors introduced the fields

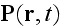 and
and

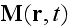 as
if they are already averaged over the REV. More on that - they use in further
derivations until the macroscopic equations these
as
if they are already averaged over the REV. More on that - they use in further
derivations until the macroscopic equations these

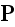 and
and

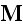 as
those already being averaged!
as
those already being averaged!
In p. 39 one can continue reading the simplifications of the
expression for an averaged macroscopic force in a body:
"We proceed to simplify this in various ways. First, we use one of Maxwell's
equations to obtain
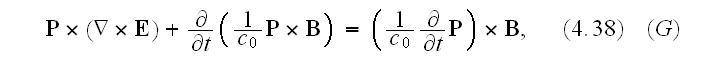
and then we use the identity
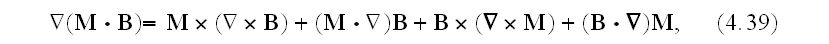
which is a generalization of (4.34)."
Our comments:
Well, here in (4.39) used the full formula for gradient of scalar product of
vectors. Why is that taken in full swing unlike before in (4.33), (4.34)?
But how can we use the "one of Maxwell's equations" if all those are still for
the atomic (microscale) level - but here we have the mathematical expressions
for fields "averaged" so far over a single separate atom in

 and
and

 ?
?
In p. 39 one can continue:
"All subsequent steps involve the statement that the integral is extended over
a volume that includes the whole body, so that, on the bounding surface of
that volume,

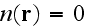 .
This means that in performing partial integrations through the use of the
divergence theorem (Gauss-Ostrogradsky homogeneous theorem;
outlined by us) the surface integrals vanish. In effect, then,
.
This means that in performing partial integrations through the use of the
divergence theorem (Gauss-Ostrogradsky homogeneous theorem;
outlined by us) the surface integrals vanish. In effect, then,
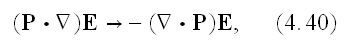
and similarly, using

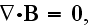

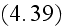 yields
yields
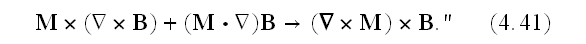
Our comments:
The important notice can be made on these transformations is that the use of
Homogeneous Gauss-Ostrogradsky theorem for the all
body of interest being bounded by REV surface - means bringing the problem to
the bulk, but still as for the point-like assessment of the physics. And
actually not worth for further consideration as of the averaged at the Upper
scale but space dependent problem.
In this case - the problem of internal electrodynamics governing equations for
the piece of material, piece of matter, but not of a dot-mass weighted
task.
And again - How we can use the atomic scale Maxwell equations for the not
averaged or only one atom averaged expression in (4.41)?
Further in p. 39 one can continue:
"The immediate result is
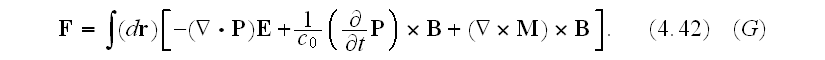
The comparison of this with the microscopic description of the force on charge
and current densities, (3.8) for zero magnetic charge, suggests the definition
of an effective charge density,

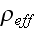 ,
and an effective current density,
,
and an effective current density,

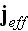 ,
as
,
as
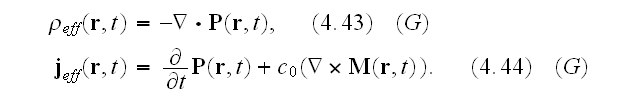
Notice, that these effective densities satisfy the equation of charge
conservation,
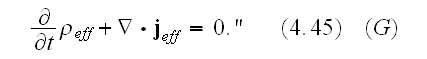
Our comments:
Notice first that in

 the fields
the fields

 and
and

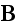 are
not the averaged over the REV or over the another non-identified volume of
averaging; not, they are the fields averaged over a separate single atom at a
location within a REV.
are
not the averaged over the REV or over the another non-identified volume of
averaging; not, they are the fields averaged over a separate single atom at a
location within a REV.
Note also, that in all these

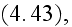

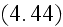 the
fields
the
fields

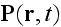 and
and

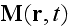 are actually the electric polarization and magnetization of a
separate atom or molecule, that's it. These are not
the averaged functions, indeed.
are actually the electric polarization and magnetization of a
separate atom or molecule, that's it. These are not
the averaged functions, indeed.
These are given in an expression as BEFORE averaging determined.
But later on, we see that they will be taken as the already averaged over the
volume of the REV functions.
******************************************************************
Schwinger at el. (1998) wrote further on the
Macroscopic form of Maxwell-Lorentz set of equations:
In p. 40-41 one can read that:
" The microscopic regime is characterized by rapid space-time variations
unlike the macroscopic one, which is characterized by scales large compared to
those of atoms. Laboratory instruments, being large, directly measure average
quantities. Macroscopic fields are thus defined in terms of averages over
space and time intervals, V and
T, large on the atomic scale but small compared to
typical macroscopic intervals. We adopt the convention that lower-case
letters, like f(r
,t), represent microscopic quantities while capital
letters, like F(r
,t), represent the corresponding macroscopic
quantities. The connection between the two is
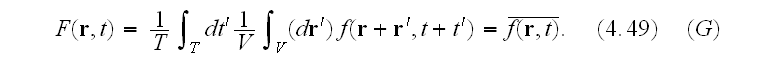
This is a linear relation, in the sense that
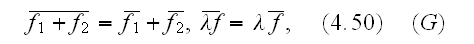
where

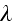 is a constant. From this follows the connection between derivatives of
microscopic and macroscopic quantities, that is, that the averaged derivative
of a function is the derivative of the average:
is a constant. From this follows the connection between derivatives of
microscopic and macroscopic quantities, that is, that the averaged derivative
of a function is the derivative of the average:
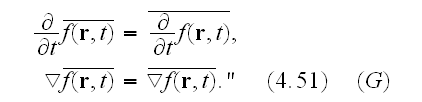
Our comments:
Here it is the very important to note and observe the
following two issues:
1) The first is that the real averaging volume - Representative Elementary
Volume (REV) has never been described or even briefly illustrated
in homogeneous physics.
Even there is no figure that students can locate in textbooks (if anyone find and
point me out the place of publication, I will comment on that).
And this is common in orthodox homogeneous physics - researcher, reader or
student can be easily driven into a variable false constructions in need at any
moment. Mostly in atomic and particle physics this is the frivolous REV - most
often the REV that is so large that it embraces the whole subject, piece of
matter, material that is under investigation. This is done to declare many
surficial integrals equal to zero.
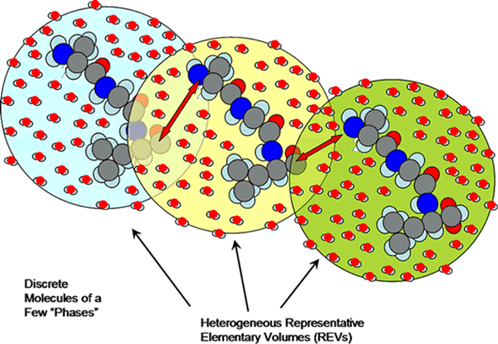
Figure 2: Polypeptide chains between
alanine, glycine and valine in aqueous solution.
Also we leave here for comparison, and for interest, in this figure
the WRONG IMAGES for water molecules -
as the unstructured 3 circles known in COHP. Comparison see in Figure 4.
The idea of Bottom-Up Scaleportation in HSVAT is one of the main concepts of
scale dependent physical and math modeling started in the 60s.
In Homogeneous physics - like in
the tested in this section monograph by
Schwinger et al. (1998) and others, there are no mathematical methods,
specifics, theorems to
do averaging over these kinds of real form REVs, and even there are no definitions
or wrong definitions
(as in Continuum Homogeneous Mechanics) of a REV.
That is the recent design of
coarse-graining sequence algorithms of
"Superatoms" in chemistry of polymers is taken from the hierarchical
scaled methodology developed in Hierarchical Scaled
Fluid Mechanics and Thermal
physics in 80s-90s, while using only chemical specific
homogeneous techniques - which is the incorrect averaging.
The very important reason to hide and not specify the
REV for this kind of averaging is obvious from the averaging construction (by
Lorentz) of Atomic scale (microscale) Maxwell-Lorentz equations when for the
key averaged terms

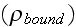 and
and

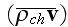 at the end needs to be fixed (fitted) the mathematical expressions for
surficial integrals in a way that nullify the very important terms that we need
to retain for correct integration.
at the end needs to be fixed (fitted) the mathematical expressions for
surficial integrals in a way that nullify the very important terms that we need
to retain for correct integration.
In this way the equations are brought to the
homogeneous continuum media form obtained by Lorentz and that
form is incorrect.
All subsequent effort in atomic physics should
followed these simplifications by Lorentz to get the same bulk continuum media
electrodynamics equations - as we know them for more than 110 years.
This misfortunate situation lasts for so long
because the proper mathematical tools for heterogeneous media averaging were
not at disposal of Lorentz.
2) The formulae

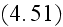 hide the important features of averaging for multiphase heterogeneous media.
hide the important features of averaging for multiphase heterogeneous media.
Generally, these formulae are not correct for
Heterogeneous media. That is why the orthodox conventional physics for so many
years since 1967 and during the following in the 80-90s developments in the
HSP-VAT tried to hide, suppress and silence the truthful physics and
mathematics of multiphase microscale theory, modeling with averaging and
scaleportation, presented in the HSP-VAT methods and math.
Because in this way all these constructions of
averaging in atomic, particle physics, and continuum mechanics as given above
for only this example of averaging Maxwell-Heaviside-Lorentz
equations, are falsified.
And they have been falsified anyway, because the correct physical and
mathematical methods of HSP-VAT have been already proven for many problems that
homogeneous methods just bring approximate
and often misleading incorrect results..
See in our -
and in
plus achievements updated up to 2004-2005 (we do more on that
- not all achievements can be stood plainly up-front):
and other pages of our websites.
Meanwhile, all other conventional textbooks on electrodynamics
and materials science show the same type of mathematical procedures for
heterogeneous averaging.
And this falsified electrodynamics lies in the
very core of the Contemporary Orthodox Homogeneous physics (COHP) - from
particle and atomic physics up to astrophysics of "Big Bangs" and
"Black Holes," etc.
One can read further in p. 41 that:
"What is the macroscopic role of the bound charge distributions? It must be
related to the effective charge and current densities given in terms of the
polarization and magnetization by (4.43) and (4.44)
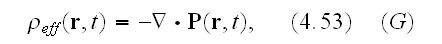
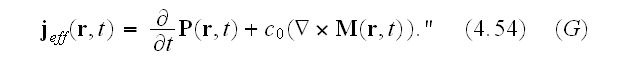
Microscale "Equations of Ampere-Maxwell for induced magnetic field and Gauss
law for electric field
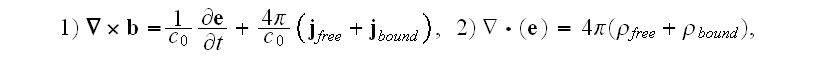
Faraday law of induction equation and Gauss law for magnetic field equation
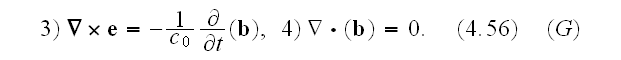
Our comments:
Here authors instantly substituted the magnetic field

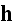 for the magnetic induction field
for the magnetic induction field

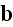 in the equations 1), 3) and 4); which is an innocent
procedure only in the "vacuum" when
in the equations 1), 3) and 4); which is an innocent
procedure only in the "vacuum" when

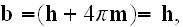 with magnetic dipole moment is
with magnetic dipole moment is

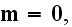 and
and

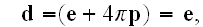 because the electric dipole
moment
because the electric dipole
moment
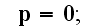 and
and

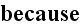 there
is no still averaging performed over the REV volume!!
there
is no still averaging performed over the REV volume!!
But they can not do changing field

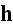 for
for

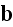 BEFORE averaging over the media with other than vacuum components, and we
provide the averaging arguments against this move.
BEFORE averaging over the media with other than vacuum components, and we
provide the averaging arguments against this move.
One of these arguments is that authors need to embed the field

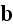 in other equations also like
in other equations also like

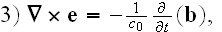 and
and

 where
where

 is not present just at the beginning before averaging will start. All these
three equations are
is not present just at the beginning before averaging will start. All these
three equations are
Also, in this way of formulating the microscopic EM equations authors avoid
appearance of convective term as

 in the equation of Ampere-Maxwell of induced magnetic field.
in the equation of Ampere-Maxwell of induced magnetic field.
Then authors immediately obtained the "averaged" equations which in reality
are the adjusted to look like "averaged" by Lorentz the known equations of macroscopic
electrodynamics:
"These are averaged to yield the macroscopic equations,
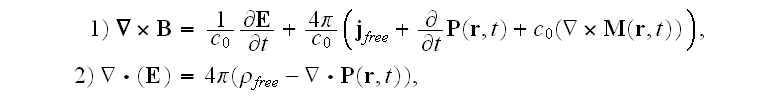
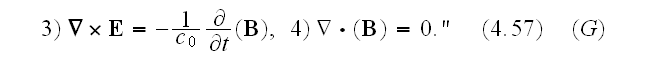
With the capital letters for averaged fields.
Our comments:
The important thing here is that the fields

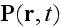 and
and

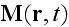 that
were not averaged within the previous set of microscopic equations
that
were not averaged within the previous set of microscopic equations

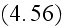 became
INSTANTLY averaged (How come?) in this set
became
INSTANTLY averaged (How come?) in this set

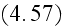 .
.
Which is the magic action indeed.
We followed here all the actions authors of point-like particles obtained for
justifying the conventional continuum Maxwell-Heaviside-Lorentz EM equations throughout
the last ~100 years since Lorentz' pseudo-averaging of microscale EM
equations, and of ~80 years since Dirac's theory of electron and quantum
mechanics induced for the point-like particulate media in particle physics.
In p. 42 finally authors get the Maxwell-Lorentz equations
written in traditional Lorentz' form:
" The final form of the historical, macroscopic Maxwell-Heaviside-Lorentz equations is
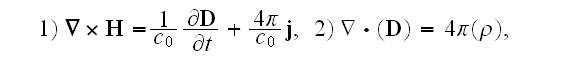
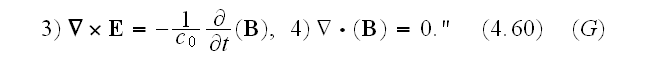
Our comments:
Returning back the notation of Ampere-Maxwell for induced magnetic field
equation

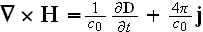 to
the original form with
to
the original form with

 that was at microscale artificially turned into
that was at microscale artificially turned into

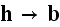 just at the beginning of averaging procedures. And with no explanation, note!
just at the beginning of averaging procedures. And with no explanation, note!
Two-Scale Bottom-Up Averaging of Maxwell-Heaviside-Lorentz
Equations (with Partial Time Derivatives)
From the Sub-Atomic Scale (~10^(-15)m) Up
to Polyatomic, Polymolecular Few Phase Medium (Material)
with the Upper Scale ~10^(-(7-6))m [Sc]
First of all the reservation we would like to pursue regarding the
inconsistency of the format of Maxwell-Lorentz equations, experimental base
for their appearance and the mathematics behind their writings. We will continue
developments on that in the another sub-sections of this section on Hierarchical
Scaled Electrodynamics.
As well as in the "Particle Physics" and "Particle Physics 2" sections.
And that is apart of the primary talk here on the averaging of atomic
scale mathematical equations up to the meso-scale space continuum formulation.
There have been discussions and disputes throughout the most of the time of the Maxwell-Heaviside-Lorentz
governing equations existance about what is the ground and a sense for these equations form.
Mainly for the two most important and used everywhere and for most often
situations - at the atomic scale for the atomic, sub-atomic applications and
at the scale of homogeneous medium of perfect (not only as perfect) crystal
constructed (or other materials) while for start adopted as a homogeneous at
the nearest to the atomic scale - the scale of crystalline structure of solid
state matter.
It might be as of

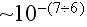 [m] and of larger scale of consideration.
[m] and of larger scale of consideration.
Initial Arguments for a "Vacuum" and Particle "Phase"
Two-Scale Averaging and Bottom-Up Scaleportation from Atomic Scale to
Meso-scale of a Substance for Maxwell-Heaviside-Lorentz Electrodynamics Equations
In all known up to now averaging procedures used in atomic, particle physics,
electrodynamics applied the postulates specified above plus the medium of vacuum.
This medium, as appeared through the many decades of research, is not an
absolute empty space. It has characteristics
from which we are interested in now that are
common electromagnetism properties as the speed of light

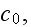 dielectric permittivity
dielectric permittivity

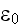 ,
and magnetic permeability
,
and magnetic permeability

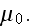
Media and Constitutive Elements (Particles)
We will use the atomic scale (microscale) as the ground base for Lower scale
electromagnetism mathematical formulation in form of Maxwell-Lorentz
equations.
We won't take right now into account other known particles apart of the
photons, electrons, nuclei; plus atoms and simple molecules. Adding these
kinds of media to a "vacuum" we mean for this development that we are assuming
still that all phenomena of the lower than

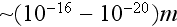 scale are taken here as of a material's components properties, and the real vacuum
(empty space) does not exist as appeared throughout the findings of others.
scale are taken here as of a material's components properties, and the real vacuum
(empty space) does not exist as appeared throughout the findings of others.
That means the fields we are describing with the scale resolutions of

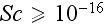

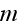 are considered as "mean" and are averaged of the fields that are of the Lower
scales.
are considered as "mean" and are averaged of the fields that are of the Lower
scales.
Particles of atomic world are of extended volume no matter how small they are,
we consider the point-like particles assumption that prevailed in the first
half of XX century as the temporary fogging of the physicists minds.
The point particles were invented at the beginning of XX century in
theoreticians circles as for convenient solution of the tasks with particles
embedded into a unified field of interest. In that way there is no particle
"field" any more. Only the volumetrically distributed mixture (homogenized) of
point-particles and of vacuum or air, for example, field.
This theoretical point of view on particles influence quickly gained a stature
via this mixture ideology. The famous mathematical tool by Dirac - the

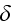 -function
was created for this purpose to connect the physical presence and location of
particles and for that do not work with the volumetric "particle" phases while
communicating to quantum mechanics linear statistical operators, these are
much easier to work with as the just mathematical points in the space.
-function
was created for this purpose to connect the physical presence and location of
particles and for that do not work with the volumetric "particle" phases while
communicating to quantum mechanics linear statistical operators, these are
much easier to work with as the just mathematical points in the space.
In its turn the quantum mechanics whole existence is based on the point-like
particles to treat those as merely statistical objects, events, which was
really simplifying and workable idea in theoretical constructions for the
times of 1920-1940s.
1) We consider as a medium number one the "active" vacuum that is being
understood as a medium filling all voids in between CBR photons, other
photons, other particles as electrons, within atomic "volumes", and in between
the "atomic" volumes and "free" space. Atomic "volumes" are the volumes of
actual variable size, as soon as outer electron shells are filled at
situation.
We put some different content in the word "active" with regard of a "vacuum." It would be
correct and just to use the old physical term Aether (ether) which in some areas of physics
is just unavoidable - in Quantum Field Theories; orthodox Particle Physics itself;
Optics homogeneous. Conventional homogeneous physicists call it shamefully as a "quantum sea,"
then they just prefer the "inherent property" for what they can not explain and can not accept
the Aether's medium because of the dogmas of SR and GR.
Generally, the people should know - what they are not told in schools and universities, that the
conventional homogeneous physics has been legitimizing the fudge in physics - any adjustment
you want you can do and GO. You can get the Nobel for that.
And it is not a joke. There are many examples of this award given for illusions. Just well organized.
2) Now we can not avoid or neglect the Cosmic Microwave Background Radiation (CMBR), even
if we do not abridge ourselves saying that CMBR is the only medium that must be
taken into account as an "active" vacuum. In this consideration we avoid the
approach taken in XIX century by Maxwell and others while considering
electromagnetic fields as having no carriers. Well, Maxwell actually
thought as of kind of an aether, plus some "elements," then the "followers" have been misinterpreting
his ideas.
As of an aether that was supported by Lorentz and all major physicists at that
time while gaining a serious backing in our days, we will extend our
treatments in the future by including speculative so far models of aether into
the scaled electromagnetic phenomena theory.
3) Consider particles, including photons and electrons as the volumetric
substances as they are. Assume that electrons have the unknown changeable
volume that is bound by its surface, and which might have a spherical volume
with mass and radius. That was the point of view of its discoverer J.J.Thomson,
which must weight a lot. Then, his opinion was ridiculed later on over 30-40 years
as of an old outdated man. And that were the "Point-Mass particles" physicists - who needed
only their constructions being taken in the field as of a true value.
Nevertheless, since that time have been performed a lot of experimental work and analytical
observations. At present, the strong amount of opinions has been advanced regarding the other (ring-like,
torus volumetric) main sub-atomic first raw particles existence.
We are specifying this with more detail in the "Particle Physics" section.
In that way while having a few media (species, phases) can be derived the
Upper scale electromagnetic fields with the origin in the Lower scales fields,
matters, and physical phenomena.
We are not to be free in this analysis allowing being engaged into discussion or lengthy
analysis of issues - What are particles as electron, photon,
nuclei?
We would state for the start that the major parts of these issues are not
known yet, in spite that more than 100 years passed since the electron
discovery, thousands pages were written on the photon nature, etc.
So far for our purposes of deriving and comparing the scale dependable
Bottom-Up strict mathematical formulation of equations for electromagnetic
phenomena at atomic and continuum mechanics scales the properties spelled
above for particles and "vacuum" are almost enough for this task.
As we already shown above and in our extended studies of hundred years
attempts to deliver this averaging - that was not done correctly. That is why
we would still need to exploit the correct mathematical tools while having
advantage of current state of physics and scaled mathematics.
Scales of consideration
As soon as we consider the fields consisted of matter, that means we consider
the material substance fields - the fields of free electrons, but that field
will be constructed out of material particles with electron features, the
fields of photons, atoms, and vacuum.
Scales of interest will be:

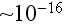 [m]
[m]
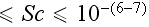 [m],
or of ten orders of decimal magnitude difference. Where the Upper scale can be
considered as of a Contimuum matter.
[m],
or of ten orders of decimal magnitude difference. Where the Upper scale can be
considered as of a Contimuum matter.
Electron, Photon and Nucleus Models, as of Scale
Dependent Particulate Media
We will add here some text and basics of including that or those models
for electron, photon, and nucleus while not to be engaged in this section
into the specifics of scaled modeling in particle physics or nuclear one.
We just want to have ability to simulate our most unusual terms
on the Upper scale where the continuum electrodynamics formulates.
Averaging and Bottom-Up Scaleportation from an Atomic Scale
to the "Continuum" like Meso-scale of Substance for
the Maxwell-Heaviside-Lorentz Electrodynamics
Equations
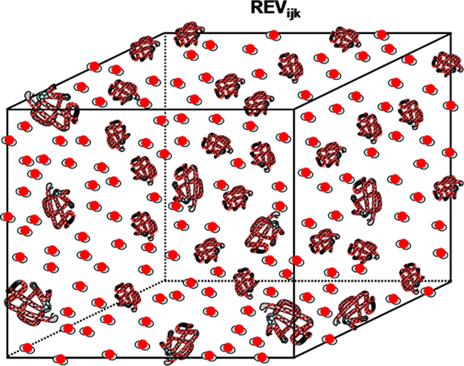
Figure 3: Three-dimensional structure REV with shown only the largest
biomonomer (myoglobin) protein molecules in an aqueous solution; water
molecules size is not scaled correctly;
also we leave here for comparison, and for interest, this figure with
the WRONG IMAGES for water molecules -
as the unstructured 3 circles known in COHP.
Note, that the molecules are free to "flow" throughout
or have been at the Bounding REV Surfaces.

Figure 4: The correct drawings for Water molecules in the
volume with the
biomonomer (myoglobin) protein molecules in an aqueous solution; water
molecules size is not scaled correctly.
Note, that the molecules are free to "flow" throughout
or have been at the Bounding REV Surfaces.
In Homogeneous physics - like in
the tested in this section monograph by
Schwinger et al. (1998) and others, there are no mathematical methods,
specifics, theorems to
do averaging over these kinds of real free and specific form REVs, and even
there are no definitions
or wrong definitions
(as in Continuum Homogeneous Mechanics) of a REV.
Through the years we've put in a number of subsections of this and other websites many conceptual advancements and written physical and mathematical models regarding Heterogeneous Electrodynamics averaging, statements and two-scale solutions -
The averaging theory (incorrect) Lorentz developed and applied toward the dielectric materials fundamentals we can observe in -
The HSP-VAT concepts and methods were applied toward atomic scale
phenomena, plasma theory and modeling -
solid state plasma modeling equations - the Lower scale equations that supposed to be already "averaged"
- unfortunately they are not averaged -
also to Heterogeneous Continuum Mechanics Electrodynamics;
that can be seen in -
as well as in our hard copy publications, some of them are in the references below.
In our further consideration we approach with scrutiny to the problem of Bottom-Up
averaging and scaleportation (strict physical and mathematical communication) from the
atomic scale Maxwell-Heaviside-Lorentz electrodynamics modeling equations up to the
continuum electrodynamics scales.
The relevant research materials have rather lengthy content (tens of pages) that
we submitting here in a concise format.
******************************************************************************
We start with the microscale simplest form of the
Gauss law magnetic field equation
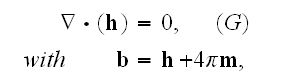
note that we can not assign

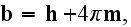 to a system of vacuum plus charges BEFORE averaging has been performed.
Thus,
to a system of vacuum plus charges BEFORE averaging has been performed.
Thus,

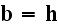 and we can write
and we can write

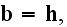 but only in CGSE
system and before averaging.
but only in CGSE
system and before averaging.
While averaging is in progress we need to sum the three functions

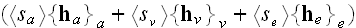 then we might have the sought after averaged value of
then we might have the sought after averaged value of

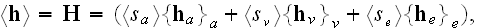 where subscripts
where subscripts

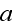 ,
,

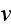 ,
and
,
and

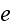 stand for atomic, "vacuum", and free electrons averaged fields and volume
fractions.
stand for atomic, "vacuum", and free electrons averaged fields and volume
fractions.
As for the atomic medium (after averaging all charges over the atoms occupied
space) - over

 where subscripts
where subscripts

 ,
,

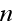 ,
and
,
and

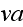 stand for bound electrons, nuclei, and "vacuum" within the atoms, molecules;
where
stand for bound electrons, nuclei, and "vacuum" within the atoms, molecules;
where

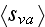 is the part of the "vacuum" within the atoms.
is the part of the "vacuum" within the atoms.
We might write (while still in the CGSE assuming
that 
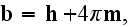 but only After averaging and at what scale? ) the Gauss law for magnetic field averaged in a matter equation as
but only After averaging and at what scale? ) the Gauss law for magnetic field averaged in a matter equation as
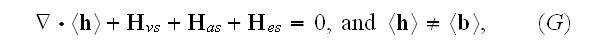
where the surficial quantities of magnetic fields

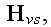

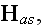 and
and

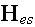 are reflecting the interaction of medium ("phase") related averaged magnetic
fields in a "vacuum", free electrons and atoms as the separate "phases."
are reflecting the interaction of medium ("phase") related averaged magnetic
fields in a "vacuum", free electrons and atoms as the separate "phases."
Notice, that there is no complete field of
induction

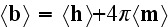 as in homogeneous pseudo-averaging obtained for this Gauss law for magnetic
field equation, but only the full averaged magnetic field
as in homogeneous pseudo-averaging obtained for this Gauss law for magnetic
field equation, but only the full averaged magnetic field

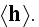 This result has been obtained by heterogeneous averaging for the Upper scale
form of this equation.
This result has been obtained by heterogeneous averaging for the Upper scale
form of this equation.
****************************************************************
Averaging over the polyphase material's media of the Gauss law for
electric field equation
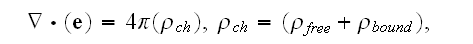
then we can have for dielectrics while using the conventional model for

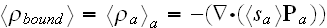 the following equation
the following equation
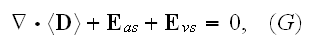
as soon as we can write the atomic phase displacement field

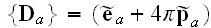 and averaged displacement field as
and averaged displacement field as

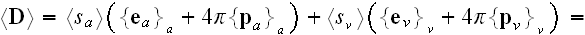

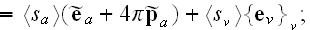 as long as in the "vacuum" the polarization vector
as long as in the "vacuum" the polarization vector

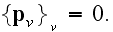
In this averaged Upper scale equation the surficial quantities of electric
fields

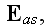

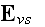 are
reflecting the interaction of medium ("phase") related averaged electric
fields in a "vacuum" and atoms, molecules as the separate "phases."
are
reflecting the interaction of medium ("phase") related averaged electric
fields in a "vacuum" and atoms, molecules as the separate "phases."
Note, that this is incomplete equation, because was used the
pseudo-averaged homogeneous model for the average charge, the averaged Upper scale
equation already has the two terms unknown in homogeneous physics for the
conventional Gauss law electric field for continuum media.
Nevertheless, when we have to use more correct and exact modeling for the

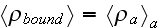 we get for the averaged continuum medium Gauss law electric field equation
we get for the averaged continuum medium Gauss law electric field equation
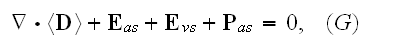
different again from the conventional continuum Upper scale equation, where

 is the polarization interface averaged term.
is the polarization interface averaged term.
*******************************************************************************
The heterogeneous microscale (atomic scale)
equation of Ampere-Maxwell for
induced magnetic field
is the second magnetic field equation
in the media for Averaging
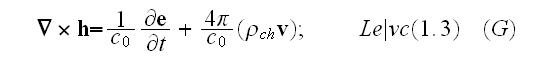
that after averaging over the sub-volumes of "vacuum," atoms, molecules, and
free electrons becomes rather complicated forms with multiple variants
actually for almost any kind of media.
The one is for the forms for the dielectrics with the weak influence of
external fields
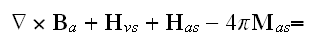
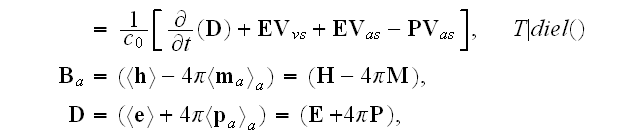
where

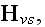 and
and

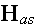 are the two terms
that
are the two terms
that
 are
reflecting the interaction of medium ("phase") related averaged magnetic
fields in a "vacuum" and atoms as the separate "phases";
are
reflecting the interaction of medium ("phase") related averaged magnetic
fields in a "vacuum" and atoms as the separate "phases";

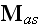 is the average of magnetic orbital momentum of outer "shell" of atoms;
is the average of magnetic orbital momentum of outer "shell" of atoms;
while

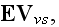

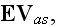

 and
and

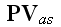 are
the terms with average electric fields at atom-"vacuum" interface
are
the terms with average electric fields at atom-"vacuum" interface
and polarization average over the interface with the speed of the interface
between the outer "shells" of atoms and "vacuum" displacement in a material.
For this averaged equation we can write the
following summary:
1) We obtained 6 additional atomic scale
morphology related and explained terms in the averaged Upper continuum scale
Ampere-Maxwell equation for induced magnetic field. These terms should extend
our abilities in understanding, modeling and design of materials, media.
2) Notice, that these effects as of

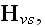

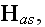

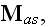

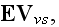

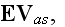 and
and

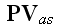 are
just absent in the homogeneous physics Maxwell-Lorentz continuum
electrodynamics equations.
are
just absent in the homogeneous physics Maxwell-Lorentz continuum
electrodynamics equations.
3) Notice, that there is NO ONE additional
coefficient appeared in the continuum equation - that means we should seek
the effective coefficients based on the only fundamental properties at atomic
scale of constituents atoms, "vacuum", and of morphology of materials at
atomic scale.
This was never achieved before.
4) Notice, that the magnetic induction field
in the averaged Ampere-Maxwell equation for induced magnetic field
is written
as
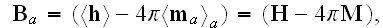 or
the sign before magnetization is proven as it is reversed to the notation used
in homogeneous physics (started from averaging by Lorentz) because in
homogeneous physics the field
or
the sign before magnetization is proven as it is reversed to the notation used
in homogeneous physics (started from averaging by Lorentz) because in
homogeneous physics the field

 instantly is replaced by
instantly is replaced by

 just before
an averaging even being declared - which is incorrect.
just before
an averaging even being declared - which is incorrect.
5) Up to this development the communication
between the atomic scale microstructure and microfields and continuum medium
morphology and effective properties were based on the approximate tools
followed the incomplete (incorrect to some extent) Maxwell-Heaviside-Lorentz macroscale
(continuum) equations.
****************************************************************
The Faraday law of induction equation
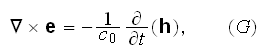
while averaged over our heterogeneous polyphase polyatom material REV; then we
can finilize with the notations as
(
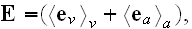

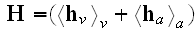 and get averaged equation for the Faraday law of induction for
dielectrics
and get averaged equation for the Faraday law of induction for
dielectrics
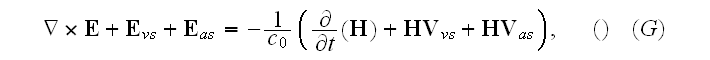
with the four heterogeneous interface surface averaged terms. These terms

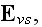 and
and

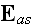 are the two terms
that
are the two terms
that
 are
reflecting the interaction of medium ("phase") related averaged electric
fields in a "vacuum" and atoms as the separate "phases"; while
are
reflecting the interaction of medium ("phase") related averaged electric
fields in a "vacuum" and atoms as the separate "phases"; while

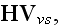

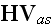

 are
the terms with average magnetic fields at atom-"vacuum" interface average over
the interface with the speed of the interface between the outer "shells" of atoms and
"vacuum" displacement in a material.
are
the terms with average magnetic fields at atom-"vacuum" interface average over
the interface with the speed of the interface between the outer "shells" of atoms and
"vacuum" displacement in a material.
For this averaged equation we can write the
following summary:
1) We obtained 4 additional atomic scale
morphology related and explained terms in the averaged Upper continuum scale
Faraday law of induction equation. These terms should extend
our abilities in understanding, modeling and design of materials, media.
2) Notice, that these effects as of

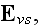

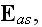

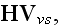

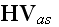 are
just absent in the homogeneous physics Maxwell-Lorentz continuum
electrodynamics equations.
are
just absent in the homogeneous physics Maxwell-Lorentz continuum
electrodynamics equations.
3) Notice, that there is NO ONE additional
coefficient appeared in this continuum equation - that means we should seek
the effective coefficients based on the only fundamental properties at atomic
scale of constituent's atoms, "vacuum", and of morphology of materials at
atomic scale. Plus the external fields influence.
This was never achieved before.
4) Notice, that there is no magnetic induction
field

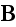 in the right hand side of this equation, but only averaged
in the right hand side of this equation, but only averaged

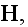 as soon as in homogeneous physics the field
as soon as in homogeneous physics the field

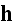 instantly is replaced by
instantly is replaced by

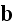 just before
an averaging even being declared - which is incorrect.
just before
an averaging even being declared - which is incorrect.
*************************************************************************************
As we can see, the equations that are resulting after averaging are hard to compare with the
conventional "bulk" media Maxwell-Heaviside-Lorentz (MHL) electrodynamics equations.
And the medium (material, substance) for which governing equations derived is
not merely the one being explained with the chemical or materials science definitions, it is given
with more strict definitions.
According to HSP-VAT the Loss and Gain Law (LGL) we can generally accept the qualitative
transformation of fields and equations. Thus the fields at one scale physical and mathematical
model and at that of even neighboring scale are different by nature of transformation by
scaleportation - that might be and of different physical nature.
We can bring
with force (making some more simplifications and equalizations) these Upper Scale
averaged (L3D) ↑(U3D) equations to the MHL form of equations for some
technical and just scientific reasons. Then, the issue will be the specifics and
theory for the "effective" coefficients for MHL kind of equations.
CONCLUSIONS:
1) All the effort spent by physicists in XX century when for justifying the
appearance of Maxwell-Heaviside-Lorentz electrodynamics macroscale (of Continuum
Mechanics) equations was to find out the appropriate or approximate
mathematical procedures which can be called "fixing" for making way to
pseudo-average the atomic scale Lorentz electromagnetism equations and present
them looking as the macroscale equations also by Lorentz, but for which
Lorentz could not use the correct averaging mathematics and physics of the end
of XX century.
Up to now physicists had not used the correct scaled averaging methods for
atomic scale Maxwell-Heaviside-Lorentz electrodynamics equations.
2) Because the problem of averaging of the array of fields and forces of
moving atoms, molecules, free electrons, photons embedded in a medium that can be
called vacuum (and is not really empty space) is the problem of scaled
heterogeneous physics, it should be treated with the tools of that physics,
including first of all the various Volume-Surface integration theorems, developed
for Heterogeneous media.
That is why the methods used in homogeneous physics in XX century must fail
and have failed to develop the correct macroscale medium (Continuum Mechanics)
electrodynamics governing equations.
3) What is used right now in physics as for the macroscale continuum homogeneous medium,
and not only homogeneous, are the Maxwell-Heaviside-Lorentz electrodynamics equations that is the
statement that has been adjusted to the form developed by Lorentz after discovery of
electron and that is the incomplete governing equations set for electromagnetism
phenomena.
There are written the huge amount of documents, papers, books on evidences
on inconsistency and disagreement of modeling using these governing equations with
experiments. These evidences continue to be ignored by conformal physics establishment
(the reasons are also known and said of many times)
and that precludes the purposes of higher standards of education, exclude chances
for basic science breakthroughs, understanding of many puzzling effects and inventions.
4) There are two methods used in homogeneous physics for pseudo-averaging of atomic
scale Maxwell-Heaviside-Lorentz electrodynamics equations: a) is the expansion in series of
the difficult terms that need to be averaged and with the great simplifications
(unacceptable) forcefully bring mathematical expressions to the Maxwell-Heaviside-Lorentz
conventional continuum mechanics set of equations; b) starting from the one atom
averaging of forces the following line of derivation using the mixed methods of
unacceptable simplifications along with the recursive use of known Maxwell-Heaviside-Lorentz
equations - the same equations that not yet been averaged in an algorithm.
Still, the worst thing in both approaches is that used the incorrect formulae for
averaging of differential operators.
5) Generally, these averaging formulae and pseudo-averaged EM governing equations used up to
now in homogeneous microscale electrodynamics, are not correct for atomic scale, for
the Upper scales averaging, for Heterogeneous media. That is why the orthodox
conventional physics for so many years since 1967 and during the following in
the 80-90s developments in the HSP-VAT tried to ignore, suppress and silence the
truthful physics and mathematics of multiphase microscale electrodynamics theory,
modeling with averaging and scaleportation, presented in the HSP-VAT methods and math.
Because of this way of homogeneous averaging in atomic and particle physics as
given above for averaging of Maxwell-Heaviside-Lorentz equations, the Upper scale
(continuum mechanics) equations have been falsified and are incomplete.
All conventional textbooks on electrodynamics and materials science are showing the same type
of incorrect mathematical procedures for heterogeneous averaging. Well - this is actual
cheating on the students and general public, professionals in various sciences and technologies!
Meanwhile, this falsified electrodynamics that is
being adjusted for every case, lies in the very core of the Contventional
Orthodox Homogeneous physics (COHP) - from particle and atomic
physics up to astrophysics.
6) Lorentz himself in his "Clerk Maxwell's Electromagnetic Theory.
The Rede Lecture for 1923, Cambridge" (1923) used to say that:
"Will it be possible to maintain these equations? I am not thinking here
of the comparatively slight modifications that have been necessary in
the theory of relativity;.....
A greater and really serious danger is threatening from the side of the
quantum theory, for the existence of amounts of energy that remain
concentrated in small spaces during their propagation, to which several
phenomena seem to point,
is in
absolute contradiction
to Maxwell's equations.
However this may be, even if further development should require
profound alterations, Maxwell's theory will always remain a step of
the highest importance in the progress of physics."
where he was citing Maxwell himself:
"It appears to me that while we derive great advantage from the recognition
of the many analogies between the electrical current and a current
of a material fluid, we must carefully avoid making any assumption not
warranted by experimental evidence,......
A knowledge of these things would amount to at least the beginning
of a complete dynamical theory of electricity, in which we should regard
electrical action, not, as in this treatise, as a phenomenon due to an
unknown cause, subject only to the general laws of dynamics,
but as the
result of
known motions of known portions of matter,
in which not only the total effects and final results, but the
whole intermediate mechanism and details of the motion,
are taken as the object of study."
7) We obtained the additional terms based on
averaging heterogeneous media techniques for every atomic scale
electrodynamics averaged
equation; for example the 6 additional atomic scale morphology related and
explained terms obtained for the averaged Upper continuum scale Ampere-Maxwell
equation for induced magnetic field. These and other equations terms should
extend our abilities in understanding, modeling and design of materials, media.
8) Notice, that these effects as of

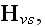

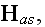

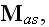

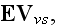

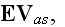 and
and

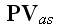 for
Ampere-Maxwell equation are just absent in the homogeneous physics
Maxwell-Heaviside-Lorentz continuum electrodynamics equations.
for
Ampere-Maxwell equation are just absent in the homogeneous physics
Maxwell-Heaviside-Lorentz continuum electrodynamics equations.
9) Notice, that there is no complete field of
magnetic induction

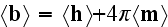 as in homogeneous pseudo-averaging obtained for the Gauss law for magnetic
field equation, but only the full averaged magnetic field
as in homogeneous pseudo-averaging obtained for the Gauss law for magnetic
field equation, but only the full averaged magnetic field

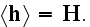 This result has been obtained by heterogeneous averaging for the Upper scale
form of this equation.
This result has been obtained by heterogeneous averaging for the Upper scale
form of this equation.
10) Notice, that the magnetic induction field in the
Ampere-Maxwell equation for induced magnetic field is written
as
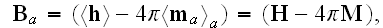 or
the sign before the magnetization term is proven as it is reversed to the notation used
in homogeneous physics Maxwell-Heaviside-Lorentz equations
(started from averaging by Lorentz) because in
homogeneous physics the micromagnetic field (of atomic scale)
or
the sign before the magnetization term is proven as it is reversed to the notation used
in homogeneous physics Maxwell-Heaviside-Lorentz equations
(started from averaging by Lorentz) because in
homogeneous physics the micromagnetic field (of atomic scale)

 instantly is replaced by the atomic scale magnetic induction field
instantly is replaced by the atomic scale magnetic induction field

 just before
an averaging even being declared - which is incorrect.
just before
an averaging even being declared - which is incorrect.
Meanwhile, there is no atomic scale magnetic induction field

 unless we either making a "SPECIAL" theory related to a separate particle (electron, nucleus)
and only, or
have been averaged the field over the some specified volume
that would include the "vacuum" and the particles, but not a homogenized
unknown one "phase" which is called vacuum (and which is the mix of "vacuum"
and of smeared particles presented as volumeless "dot-points")
- as of an atom or
of larger dimension as the REV and have already received that field
unless we either making a "SPECIAL" theory related to a separate particle (electron, nucleus)
and only, or
have been averaged the field over the some specified volume
that would include the "vacuum" and the particles, but not a homogenized
unknown one "phase" which is called vacuum (and which is the mix of "vacuum"
and of smeared particles presented as volumeless "dot-points")
- as of an atom or
of larger dimension as the REV and have already received that field

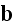 as a result of averaging with all components of this
as a result of averaging with all components of this

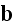 field, but obtaned as by averaging and shown as
averaged either over the atom or the REV.
Otherwise, the instant unjustified change of
field, but obtaned as by averaging and shown as
averaged either over the atom or the REV.
Otherwise, the instant unjustified change of

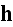 with
with

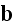 is just the "fixing" to the Lorentz form of continuum scale equations.
is just the "fixing" to the Lorentz form of continuum scale equations.
11) Notice, that there is no magnetic induction
field

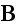 in the right hand side of the Faraday law of induction
equation, but only the averaged
in the right hand side of the Faraday law of induction
equation, but only the averaged

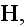 again because in homogeneous physics the field
again because in homogeneous physics the field

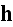 instantly is replaced by
instantly is replaced by

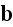 (see
in each atomic physics, electrodynamics textbook) just before an averaging
even being declared - which is incorrect.
(see
in each atomic physics, electrodynamics textbook) just before an averaging
even being declared - which is incorrect.
12) Notice, that there is NO ONE additional
coefficient appeared in the continuum equations for the Upper scale - that means
we should seek the effective coefficients based on the only fundamental
properties at atomic scale of constituent's atoms, "vacuum", and of morphology
of materials at atomic scale. Plus the external fields influence.
This was never achieved before.
13) Up to this development the communication
between the atomic scale microstructure and microfields and continuum medium
morphology and effective properties were based on the approximate tools
followed the incomplete (incorrect to some extent) Maxwell-Heaviside-Lorentz macroscale
(continuum) equations.
14) There would be many formulations in electrodynamics for different matters
and for different scales. Not as of the case that used right now which is
the application of the same kind of Lorentz' Continuum Mechanics electrodynamics
equations for any scale and any medium. Just using changed coefficients that
are the adjusting parameters right now.
15) As one can observe, the Upper scale continuum averaged electrodynamics equations that
have the Lower scale MHL equations, can be classified as the set of integro-differential
equations. One can derive on their base the numerous implementations reflecting the specific
physical task. That is the way to evaluate the standard test specific property "bulk"
coefficients for conventional homogeneous medium electrodynamics.
This problem is of incredible value itself.
16) The Upper scale averaged atomic scale fundamental electrodynamics
equations should help to design experiment(s) aiming at study of electrons
outer atomic shell spatial distribution and morphology.
17) The same kind of pseudo-averaging (continuum mechanics derivation within itself)
was brought into the contemporary models, mathematical
formulation in hydrodynamics that are the partial differential equations for hydrodynamics
phenomena - as the Navier-Stokes equations for laminar flow.
Having these incorrect averaging procedures from atomic to continuum mechanics formulation
as those used for Maxwell-Heaviside-Lorentz electrodynamics equations (besides of that, there was
no knowledge about the structure of atoms and molecules at the time of Stokes,
other physical and mathematical schemes of XX century are not qualified for correct
scaleportation of momentum and impulse as well);
it is not surprising that
the oldest unsolved problem in physics called the turbulence explanation and its dynamics
formulation has not been solved and can not be solved based on the accepted now
laminar form equations of fluid dynamics.
More than hundred years effort has given the engineering
approximations that are not suitable for phenomena inherently stated with the polyscale interactions,
as plasma modeling, for example, for projects like the ITER.
REFERENCES:
1) Hecht, L., "SHOULD THE LAW OF GRAVITY BE REPEALED? The Suppressed Electrodynamics of Ampere-Gauss-Weber,"
Editorial, 21st Century Science & Technology, Spring, (2001)
2) Hecht, L., "Science: To Be, or Not to Be Or, How I Discovered
the Swindle of Special Relativity,"
Editorial, 21st Century Science & Technology, Winter 1999-2000, (2000)
3) Hecht, L., "The Atomic Science Textbooks Don't Teach. The Significance of the 1845 Gauss-Weber Correspondence,"
Editorial, 21st Century Science & Technology, pp. 21-43, (1996)
4)
Jackson, J., Classical Electrodynamics, 3rd ed., Wiley and Sons, New York, NY,
(1999). pp. 1-808.
5)
Landau, L.D. and Lifshits, E.M., Electrodynamics of
Continuous Media,Pergamon Press, Oxford, (1960).
6)
Landau, L.D. and Lifshits, E.M., Electrodynamics of Continuous
Media, Gos. Izd. Tekh.-Teor. Lit., Moscow,
(1957). 532 pgs. (in Russian).
7)
Levich, V.G., Course of Theoretical Physics, Vol. 1, Nauka Publishing, Moscow,
(1969). 912 pgs.(in Russian).
8)
Lorentz, H.A., The Theory of Electrons and Its Applications
to the Phenomena of Light and Radiant Heat : a Course of Lectures Delivered in
Columbia University in 1906, Dover, New York, N.Y., (1952). pp. 1-343.
9)
Lorentz, Hendrik A., Clerk Maxwell's Electromagnetic Theory. The Rede Lecture
for 1923, Cambridge University Press, Cambridge, 1923. pp. 1-35.
10)
Maxwell, J.C., A Treatise on Electricity and Magnetism,
Vol. 1, 3rd Ed., Oxford University Press, New York, (2002a). pp. 1-506,
plus 14 pages with the figures attached.
11)
Maxwell, J.C., A Treatise on Electricity and Magnetism,
Vol. 2, 3rd Ed., Oxford University Press, New York, (2002b). pp. 1-500,
plus 6 pages with the figures attached.
12)
Dayton Miller, "The Ether-Drift Experiment and the Determination of the
Absolute Motion of the Earth", Reviews of Modern Physics, Vol.5(2),
p.203-242, July (1933).
13)
Dayton Miller, "The Ether-Drift Experiment and the Determination of
the Absolute Motion of the Earth", Nature, Vol.133, p.16-27, 3 Feb. (1934).
14)
Morley, E.W. and Miller, D., "Report of an Experiment to Detect
the FitzGerald-Lorentz Effect", Proceedings, Am. Acad.
Arts & Sciences, 41:321-328, (1905).
15)
Morley, E.W. and Miller, D., "Final Report on Ether-Drift Experiments",
Science, 25:525, 5, (1907).
16)
Mills, R.L., "Classical Quantum Mechanics," Physics Essays, Vol. 16, No. 4,
pp. 433-498, (2003).
17)
Mills, R.L., "Maxwell's Equations and QED: Which is Fact and Which is
Fiction,"
18)
Mills, R. L., "The Fallacy of Feynman's Argument on the Stability of the
Hydrogen Atom According to Quantum Mechanics," submitted; posted at
http://www.blacklightpower.com/theory/theorypapers/Fallacy_Feynmans_Argument_030705.pdf.
19)
Purcell, E.M., Electricity and Magnetism, Berkeley Physics Course, Vol. 2,
Nauka, Moscow, (1971). 448 pgs. (in Russian)
20)
Schwinger, J., DeRaad, L.L.Jr., Milton, K.A., and Tsai, W-y., Classical
Electrodynamics, Perseus Books, Reading, Massachusetts, (1998). 569 pgs.
21)
Smith, G.S., An Introduction to Classical
Electromagnetic Radiation, Oxford
University Press, New York, (1997). pp. 1-653.
22)
Vinogradov, A.P., Electrodynamics of Composite
Materials, Aditorial URSS, Moscow, (2001). 208 pgs.
23)
Vlasov, A.A., "On Vibration Properties of Electron Gas," J. Exp. Theor. Phys., Vol. 8, No. 3, pp. 291-, (1938). (in Russian).
24)
Vlasov, A.A., "The Vibrational Properties of an Electron Gas," Soviet Physics Uspekhi, No. 10, pp. 721- , (1968).
25)
Vlasov, A.A., "On the Kinetic Theory of an Assembly of Particles with Collective Interaction," Journal of Physics USSR, Vol. 9, No. 1, pp. 25 - 40, (1945).
26)
Vlasov, A.A., "On the Theory of the Solid State," Journal of Physics USSR, Vol. 9, No. 2, pp. 130-138, (1945).
27)
Vlasov, A.A., Many-Particle Theory and Its Application to Plasma, Gordon and Breach, New York, (1961).
28) Travkin, V.S., Catton, I., and Ponomarenko, A.T., "Three Scale Hierarchical
Modeling of Electrostatics and Electrodynamics in Porous Ferrites; Effective
Dielectric Properties and Experiments," in Proc. 5th
IUMRS-Int. Conf. Advansed Materials'99, Beijing, Vol. 2, p. 684, (1999a)
29) Travkin, V.S., and I. Catton, "Radiation Heat Transport in Porous Media,"
in Proc. ASME, HTD-364-3, Vol. 3, pp. 31-40, (1999)
30) Travkin, V.S., I. Catton, K. Hu, A.T. Ponomarenko, and V.G. Shevchenko,
(1999), "Transport Phenomena in Heterogeneous Media: Experimental Data
Reduction and Analysis", in Proc. ASME, AMD-233, Vol.
233, pp. 21-31, (1999b)
31) Ponomarenko, A.T., Ryvkina, N.G., Kazantseva, N.E., Tchmutin, I.A.,
Shevchenko, V.G., Catton, I.,and Travkin, V.S., "Modeling of Electrodynamic
Properties Control in Liquid-Impregnated Porous Ferrite Media", in
Proc. SPIE Smart Structures and Materials 1999,
Mathematics and Control in Smart Structures, V.V. Varadan, ed., Vol. 3667, pp.
785-796, (1999)
32) Travkin, V.S., Catton, I., Ponomarenko, A.T., Gridnev, S.A., Kalinin,
Yu.E., Darinskiy, B.M., (2000), "Electrodynamics and Electrostatics in
Heterogeneous Media. Effective Properties and their Assessments," in
Proc. PIERS'2000: Progress in Electromagnetics Res.
Symp., p. 1028, (2000a)
33) Travkin, V.S., Catton, I., Ponomarenko, A.T., Gridnev, S.A., Kalinin,
Yu.E., Darinskiy, B.M., (2000), "Ferromagnetism in Scaled Hierarchical
Materials. Wave Absorption on Micro- and Macroscale," in
Proc. PIERS'2000: Progress in Electromagnetics Res.
Symp., p. 1029, (2000b)
34) Travkin, V.S. and Catton, I.., "Transport Phenomena in Heterogeneous Media
Based on Volume Averaging Theory", Advances in Heat
Transfer, Vol. 34, pp. 1-144, (2001a)
35) Ponomarenko, A.T., Shevchenko, V.G., Ryvkina, N.G., Chmureva, V.V.,
Tchmutin, I.A., and Travkin, V.S., "Electrical Transport and Relaxation
Processes in Polymeric Materials: Modeling and Experimental Results",
Condensed Matter and Interfaces, Vol. 3, No. 1,
pp.73-81 (in Russian), (2001)
36) Travkin, V.S. and Catton, I., "Heat and Charge Conductivities in
Superlattices - Two-Scale Measuring and Modeling," in Proc.
Intern. Mech. Engin. Congress and Exposition (IMECE'2001),
IMECE/HTD-24260, pp.1-12, (2001b)
37) Travkin, V.S. and Catton, I., "Analysis of Measuring Techniques for
Superlattices Thermal Conductivity Measurements," in Proc.
Intern. Mech. Engin. Congress and Exposition (IMECE'2001),
IMECE/HTD-24348, pp.1-12, (2001c)
38) Travkin, V.S., Catton, I., Ponomarenko, A.T., and Kalinin, Yu.E., "Bottom
Up and Top Down, from Nano-Scale to Micro-Scale, Hierarchical Descriptions of
Electrodynamic, Thermal and Magnetic Fields in Ferromagnets and HTSCs", in
Proc. DOE 20th Symposium on Energy Engineering
Sciences, Argonne National Laboratory, pp. 296-304, (2002)
39) Travkin, V. S. and Ponomarenko, A. T., "Electrodynamic Equations for
Heterogeneous Media and Structures on the Length Scales of Their
Constituents", Inorganic Materials, Vol. 40, Suppl. 2,
pp. S128 - S144, (2004)
40) Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of
Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media,
the Two-Scale Solutions and Measurement Applications -1,"
Journal of Alternative Energy and Ecology, No. 3, pp.
7-17, (2005a)
41) Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of
Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media,
the Two-Scale Solutions and Measurement Applications - 2,"
Journal of Alternative Energy and Ecology, No. 4, pp.
9-22, (2005b)
42) Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of
Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media,
the Two-Scale Solutions and Measurement Applications - 3,"
Journal of Alternative Energy and Ecology, No. 5, pp.
34-44, (2005c)
UNDER CONTINUING DEVELOPMENT



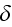 -function.
-function.

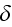 -function in 1929 there were solved two and even three tasks in atomic
physics:
-function in 1929 there were solved two and even three tasks in atomic
physics:

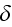 -function added greatly to the functionality of the hard solid rock of QM that is laying on
the road to further progress in physics for many decades.
-function added greatly to the functionality of the hard solid rock of QM that is laying on
the road to further progress in physics for many decades.

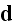 the electric force, the same symbol serving for the dielectric displacement,
because in the ether this has the same direction and, on account of the choice
of our units, the same numerical magnitude as the electric force. We shall
further represent by
the electric force, the same symbol serving for the dielectric displacement,
because in the ether this has the same direction and, on account of the choice
of our units, the same numerical magnitude as the electric force. We shall
further represent by

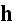 the magnetic force and by
the magnetic force and by

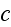 a constant depending on the properties of the ether.
a constant depending on the properties of the ether.

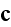 ,
which now consists only of the displacement
current of Maxwell. It exists wherever the dielectric displacement
,
which now consists only of the displacement
current of Maxwell. It exists wherever the dielectric displacement

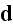 is
a function of the time, and is given by the formula
is
a function of the time, and is given by the formula
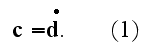
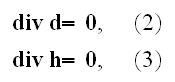
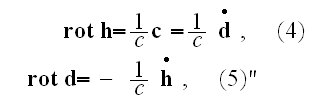

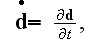

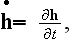 used as a partial derivative with respect to the time.
used as a partial derivative with respect to the time.

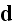 and
and

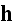 ,
where in an ether (or "vacuum") the
displacement
,
where in an ether (or "vacuum") the
displacement
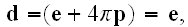 because the electric dipole
moment
because the electric dipole
moment
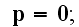 and where
and where

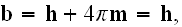 because magnetic dipole moment is
because magnetic dipole moment is

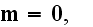

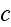 in Lorentz's physical statement is the "constant depending on the
properties..."
in Lorentz's physical statement is the "constant depending on the
properties..."

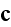 .
As to the last equation, it expresses the law according to which electric
forces are called into play in a system with a variable magnetic field, i.e.
the law of what is ordinary called electromagnetic induction. The formulae (),
() and (5) are vector equations and may each be replaced by three scalar
equations relating to the separate axes of coordinates."
.
As to the last equation, it expresses the law according to which electric
forces are called into play in a system with a variable magnetic field, i.e.
the law of what is ordinary called electromagnetic induction. The formulae (),
() and (5) are vector equations and may each be replaced by three scalar
equations relating to the separate axes of coordinates."

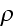 as
a continuous function of the coordinates, so that the charged particle has no
sharp boundary, but is surrounded by a thin layer in which the
density gradually sinks from the value it has within the electron to 0.
as
a continuous function of the coordinates, so that the charged particle has no
sharp boundary, but is surrounded by a thin layer in which the
density gradually sinks from the value it has within the electron to 0.

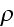 ,
which we have never to trouble ourselves about surfaces of discontinuity, nor
to encumber the theory by separate equations relating to these.
,
which we have never to trouble ourselves about surfaces of discontinuity, nor
to encumber the theory by separate equations relating to these.

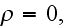 so that we have only to write down one system of differential equations.
so that we have only to write down one system of differential equations.
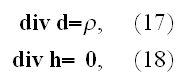
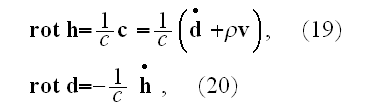

 contained within it. It is expressed by the
equation
contained within it. It is expressed by the
equation
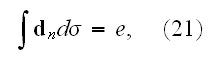

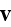 is the velocity of the charge".
is the velocity of the charge".

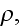 and
and

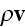 -
unless we consider the collective, averaged fields in an area.
-
unless we consider the collective, averaged fields in an area.
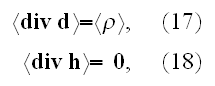
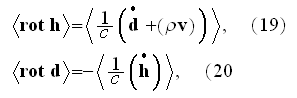
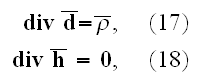
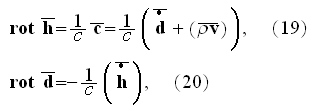

 ,
the magnetic force
,
the magnetic force

 ,
the current of electricity
,
the current of electricity

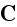 and
the magnetic induction
and
the magnetic induction

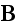 .
These are connected by the following fundamental equations:
.
These are connected by the following fundamental equations:
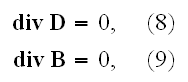
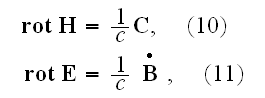

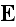 and
and

 on
the one hand, and that between
on
the one hand, and that between

 and
and

 on
the other. Confining ourselves to isotropic bodies, we can often describe the
phenomena with sufficient accuracy by writing for the dielectric displacement
on
the other. Confining ourselves to isotropic bodies, we can often describe the
phenomena with sufficient accuracy by writing for the dielectric displacement
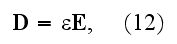
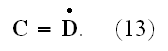
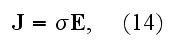

 is
a new constant. This vector is the only current and therefore identical to
what we have called
is
a new constant. This vector is the only current and therefore identical to
what we have called

 ,
if the body has only the properties of a conductor. In some cases however, one
has been led to consider bodies endowed with the properties of bothconductors
and dielectrics.
,
if the body has only the properties of a conductor. In some cases however, one
has been led to consider bodies endowed with the properties of bothconductors
and dielectrics.
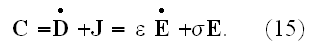
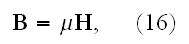

 is a new constant. "
is a new constant. "


![$[cm^{3}]$](/eldyn/incompat/IncompatMaxwell206__55.gif)