
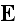 ,
the magnetic force
,
the magnetic force

 ,
the current of electricity
,
the current of electricity

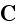 and
the magnetic induction
and
the magnetic induction

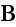 .
These are connected by the following fundamental equations:
.
These are connected by the following fundamental equations:
The Annals of Frontier and Exploratory Science
Vladi S. Travkin
Hierarchical Scaled Physics and Technologies (HSPT), Rheinbach, Germany, Denver, CO, USA
Any information displayed here is the propriatary information in the area of - What's Wrong with the Pseudo-Averaging Used in Textbooks on Atomic Physics and Electrodynamics for Maxwell-Heaviside-Lorentz Electromagnetism Equations.
This text below and information are so far a proprietary development. Any mentioning of the following should be strictly accompanied with the disclosure of this website (and/or of other our sites if applicable) and the exact context of the said information. So far it is an open information, but at any moment can be modified or deleted.
We would like to study the many claims related to the appearance of Maxwell-Lorentz electrodynamics equations at continuum scales.
**********************************************************************************
Lorentz' 1906'th Continuum Mechanics Electrodynamics Governing Equations
Lorentz (1923) on the Future Modifications of Maxwell Equations
Landau and Lifshits on Averaging of Atomic Scale Maxwell-Lorentz Electromagnetism Equations
Levich's "Averaging" of Atomic Scale Maxwell-Lorentz Equations
Electromagnetism Modeling and Maxwell-Lorentz Equations in Vlasov's Theory of Long-Range Collective Phenomena (Averaging)
Jackson (1999) Pseudo-Averaging of Atomic Scale Maxwell-Lorentz Equations
Schwinger et al. (1998) Pseudo-Averaging of Microscale Maxwell-Lorentz Equations
R.Mills' Theory of Classical Quantum Mechanics (CQM) and Maxwell Equations as a Communicator Between CQM and the Rest of Physics
What is objectionable in the CQM Theory regarding of what is being suggested:
CONCLUSIONS:
REFERENCES:
*******************************************************************************
We start with examination of Lorentz' points of view, who has done the most to establish the contemporary homogeneous format of Maxwell-Lorentz modeling equations.
The EM equations by Lorentz (1906) in a matter given as (p.7):
"4. There is one way of treating these phenomena that is
comparatively safe and, for many purposes, very satisfactory. In following it,
we simply start from certain relations that may be considered as expressing,
in a condensed form, the more important results of electromagnetic experiments.
We have now to fix our attention on four vectors, the electric force

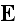 ,
the magnetic force
,
the magnetic force

 ,
the current of electricity
,
the current of electricity

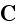 and
the magnetic induction
and
the magnetic induction

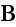 .
These are connected by the following fundamental equations:
.
These are connected by the following fundamental equations:
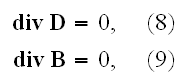
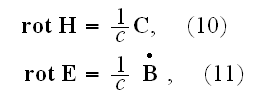
presenting the same form as the formulae we have used for the ether.
In the present case however, we have to add the relation between

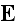 and
and

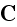 on
the one hand, and that between
on
the one hand, and that between

 and
and

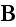 on
the other. Confining ourselves to isotropic bodies, we can often describe the
phenomena with sufficient accuracy by writing for the dielectric displacement
on
the other. Confining ourselves to isotropic bodies, we can often describe the
phenomena with sufficient accuracy by writing for the dielectric displacement
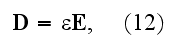
a vector equation which expresses that the displacement has the same direction as the electric force and is proportional to it. The current in this case is again Maxwell's displacement current
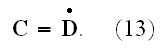
In conducting bodies on the other hand, we have to do with a current of conduction, given by
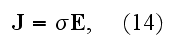
where

 is
a new constant. This vector is the only current and therefore identical to
what we have called
is
a new constant. This vector is the only current and therefore identical to
what we have called

 ,
if the body has only the properties of a conductor. In some cases however, one
has been led to consider bodies endowed with the properties of both
conductors and dielectrics.
,
if the body has only the properties of a conductor. In some cases however, one
has been led to consider bodies endowed with the properties of both
conductors and dielectrics.
If, in a substance of this kind, an electric force is supposed to produce a
dielectric displacement as well as a current of conduction, we may apply at
the same time (12) and (14), writing for the total current
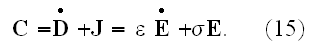
Finally, the simplest assumption we can make as to the relation between the magnetic force and the magnetic induction is expressed by the formula
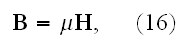
in which

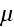 is a new constant. "
is a new constant. "
Our comments:
Note here, that there were no averaging operators at all by the Lorentz time. There were no atomic physics and the nucleus will be discovered only in 1911.
So, the mathematical formulation of the continuum electrodynamics were found based on general considerations of experiments and with the homogeneous Volume-Surface theorems by mostly as the Gauss-Ostrogradsky and Green's theorems.
But not with any kind of averaging techniques at atomic scale used for Maxwell-Lorentz equations.
In p. 8 further Lorentz gives few outstanding sentences regarding the role of modeling in electromagnetism:
"If we want to understand the way in which electric and magnetic propreties depend on the temperature, the density, the chemical constitution or the crystalline state of substances, we cannot be satisfied with simply introducing for each substance these coefficients, whose values are to be determined by experiment; we shall be obliged to have recourse to some hypothesis about the mechanism that is at the bottom of the phenomena."
More in p. 8 Lorentz writes:
"It is by this necessity, that one has been led to the conception of electrons, i.e. of extremely small particles, charged with electricity, which are present in immense numbers in all ponderable bodies, and by whose distribution and motion we endeavor to explain all electric and optical phenomena that are not confined to the free ether."
In pgs. 8-9 Lorentz writes:
"In a ponderable dielectric there can likewise be a motion of the electrons. Indeed, though we shall think of each of them as having a definite position of equilibrium, we shall not suppose them to be wholly immovable. They can be displaced by an electric force exerted by the ether, which we conceive to penetrate all ponderable matter, a point to which we shall soon have to revert."
Our comments:
In p. 9 Lorentz continues:
"Now, however, the displacement will immediately give rise to a new force by which the particle is pulled back towards its original position, and which we may therefore appropriately distinguish by the name of elastic force.
The motion of the electrons in non-conducting bodies, such as glass and sulphur, kept by the elastic force within certain bounds, together with the change of the dielectric displacement in the ether itself, now constitutes what Maxwell called the displacement current. A substance in which the electrons are shifted to new positions is said to be electrically polarized.
Again, under the influence of the elastic forces, the electrons can vibrate about their positions of equilibrium. In doing so, and perhaps also on account of other more irregular motions, they become the centers of waves that travel outwards in the surrounding ether and can be observed as light if the frequency is high enough. In this manner we can account for the emission of light and heat."
Our comments:
"Will it be possible to maintain these equations? I am not thinking here of the comparatively slight modifications that have been necessary in the theory of relativity;.....
A greater and really serious danger is threatening from the side of
the quantum theory, for the existence of amounts of energy that remain
concentrated in small spaces during their propagation, to which
several phenomena seem to point, is in

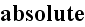

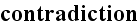 to Maxwell's equations.
to Maxwell's equations.
However this may be, even if further development should require profound alterations, Maxwell's theory will always remain a step of the highest importance in the progress of physics."
where he was citing Maxwell himself:
"It appears to me that while we derive great advantage from the recognition of the many analogies between the electrical current and a current of a material fluid, we must carefully avoid making any assumption not warranted by experimental evidence,......
A knowledge of these things would amount to at least the beginning of a complete dynamical theory of electricity, in which we should regard electrical action, not, as in this treatise, as a phenomenon due to an unknown cause, subject only to the general laws of dynamics, but as the result of known motions of known portions of matter, in which not only the total effects and final results, but the whole intermediate mechanism and details of the motion, are taken as the object of study."
Our comments:
Note that Maxwell said these words long before an electron, a nucleus, other particles, and atomic structures of matter were discovered.
It would be relevant to cite here what else Lorentz (1923) writes in p. 32:
"Maxwell did not always express himself so cautiously: at other times he did not shrink from imagining an elaborate mechanical model.
All physicists know its principal features. The magnetic energy is considered as a true vis viva, the magnetic field being the seat of invisible motions, rotations of small particles about the lines of force.
The system of these particles may be compared to a wheelwork, and Maxwell has to explain how it can be that all the wheels in an element of volume are rotating in the same direction.
This shows that the motion is not transmitted directly from one wheel to the next. So Maxwell is led to assume that between these wheels of the magnetic field and in contact with them, there are smaller ones which transmit the motion in the manner of friction wheels.
What I called wheels might in reality be spheres capable of turning about axes in any direction and, as Maxwell showed, a system of this kind is amenable to mathematical analysis. In his image the friction wheels represent what we call electricity; in a conductor we must conceive them to be freely movable, ....."
Our comments:
Yes, that might be atoms, molecules, electrons, other particles involved into magnetic fields of local and averaged (bulk) significance.
The words of Lorentz above are pretty on target regarding what was derived with the HSP-VAT application to the sub-atomic Lower scale wheelwork to get to the bulk properties and mathematical dependencies in - "Incompatibility of Maxwell-Lorentz Electrodynamics Equations at Atomic and Continuum Scales"
and
".... The outcome of these various attempts is, in my opinion, this: that we must admit the possibility of mechanical representations, a possibility that is already shown by the fact that the formulae of the electromagnetic field can be given the form of the general equations of dynamics.
On the other hand it cannot be denied that, when we desire them to be applicable to a comparatively wide range of phenomena, the theories that have proposed become so complicated that they give us but little satisfaction......"
Our comments:
What would Lorentz to say today when watching the ITER and LHC projects activities? He might's turning upside down.
In the very first page 11 (Russian publication) they wrote:
"That is, instead of real "microscopic" value of electric field strength

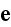 we will be considering its averaged value, determine it as
we will be considering its averaged value, determine it as
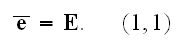
Basic equations of continuum mechanics electrodynamics usually obtained by averaging of equations of electromagnetic field in the vacuum. This transformation from micro- to macroscopic equations was firstly performed by G.A.Lorentz."
Our comments:
In p. 12 authors just boldly saying that averaging of microscopic equations

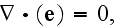 and
and

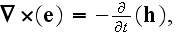 straightly bring the forms
straightly bring the forms

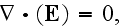

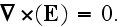 Averaging has been made mainly verbally.
Averaging has been made mainly verbally.
In the page 55 a reader can find:
"The second is made with the averaging of equation

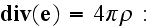
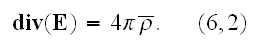
Assuming that inside dielectric substance there is none externally inserted
charges; this is the most usual and important case. Then the full charge in
the whole volume of dielectric is set equal to zero and after introduction of
it into electrical
field:
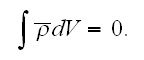
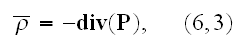
besides, outside of the body

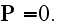 In fact, having integration over the volume that is surrounded by surface
having it inside and going everywhere outside, we will have
In fact, having integration over the volume that is surrounded by surface
having it inside and going everywhere outside, we will have
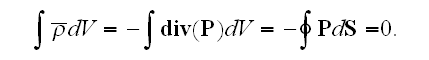
Further in the next page 12, authors derive:
"By definition of dipole moment, this is the integral
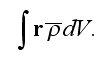
Making substitution

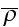 from (6,3) and taking integral
from (6,3) and taking integral

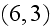 over
the volume, that is having the body within it, get
over
the volume, that is having the body within it, get
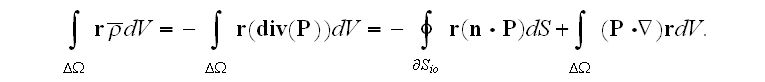
The surface integral is disappearing, and in the second one we have

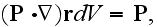 that means
that means
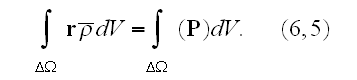
That is why the polarization vector presents itself the dipole moment ( or the electric moment) of dielectric unity volume."
Our comments:
The same derivation as in Levich (1969 we can see, only
Landau and Lifshits (1957, 1960) took that very simple with the outright
suggestion that the averaged

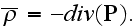
***************************************
Then, in the page 304 reader can find excerpts about the averaging process regarding the whole set of microscopic Maxwell-Lorentz equations:
"Equations
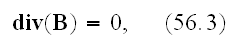
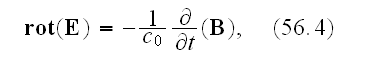
can be obtained immediately by changing

 and
and

 in exact microscopic Maxwell equations with their averaged variables
in exact microscopic Maxwell equations with their averaged variables

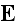 and
and

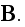 That is why these equations by no means are not needed any change. What
related to equation
That is why these equations by no means are not needed any change. What
related to equation
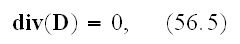
then this equation obtained with averaging of exact microscopic equation

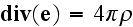 ,
besides here is used the fact that the full charge of the body equal to
zero."
,
besides here is used the fact that the full charge of the body equal to
zero."
"One more equation must be produced by averaging of the exact equation
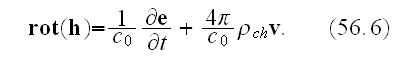
Immediate averaging gives
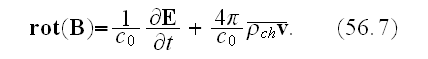
Meanwhile, when the macroscopic field is time dependent establishing the
connection of the mean value of

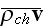 with the earlier introduced variables is pretty complicated task. It is easier
to make the needed averaging not directly, but using the following more normal
way."
with the earlier introduced variables is pretty complicated task. It is easier
to make the needed averaging not directly, but using the following more normal
way."
Then, authors make few transformations of like already "averaged" (in reality
not averaged, just declared as averaged) other equations from the Maxwell set
and bring to readers the following equation for magnetic field as the
"averaged" one
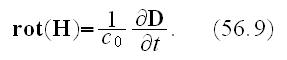
From this set (unaveraged)
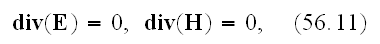
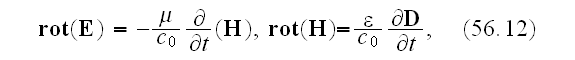
Landau and Lifshits immediately obtained the fundamental expression on the speed of electromagnetic field in the dielectrics - as the following equality
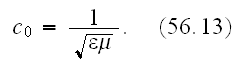
Our comments:
These exercises in formal interplaying of three Maxwell equations as of already averaged ones - but in reality just declared as "averaged," can not be considered as the averaging of microscale, atomic scale equations found from that set of electrodynamics equations.
Interesting to note that the immediate transformation of

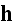 field into the
field into the

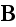 is not considered as the fault, error, etc.?
is not considered as the fault, error, etc.?
*******************************************************************
Then, at last the final text describing the no-one approach to averaging of microscopic equations by Landau and Lifshits (1957, 1960) we might cite from page 466 that:
"Electromagnetic quantities

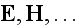 present in macroscopic electrodynamics, having obtained as the result of
averaging that can be imagined as the collection of two
operations. If to accept, for graphical picture, from the classic
point of view then that could be distinguished the averaging over the
physically infinitely small volume when the locations of all particles are
assigned and then by averaging of that value over the particles movements."
present in macroscopic electrodynamics, having obtained as the result of
averaging that can be imagined as the collection of two
operations. If to accept, for graphical picture, from the classic
point of view then that could be distinguished the averaging over the
physically infinitely small volume when the locations of all particles are
assigned and then by averaging of that value over the particles movements."
Our comments:
What does it mean - "averaging over the physically infinitely small volume" of a heterogeneous multiphase substance? Over the infinitely scaled down morphology of the same kind? Each part, each phase should be infinitely scaled down?
That was not a question in all over this book.
before averaging
for vacuum with charges-particles

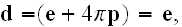

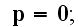
for vacuum

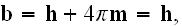

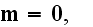 in
the CGSE system.
in
the CGSE system.
In pgs. 684-5 (Vol. 1) one can read that for microscale, atomic scale Maxwell-Lorentz equations we should use the following set:
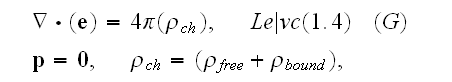
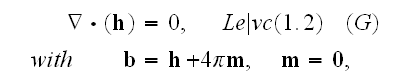
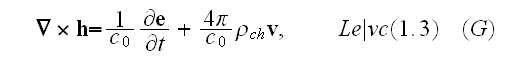
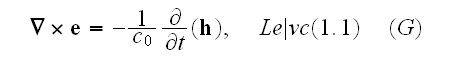
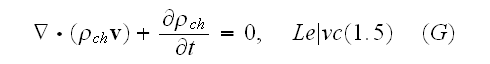
Our comments:
This set of local electrodynamics equations in a medium which consists of "vacuum" and point-particles - nuclei, electrons, we can find in Lorentz' equations - that Lorents meant in writing these kind of equations that the electrons and aether constitute the same medium just with the space depending properties with a smooth transition boundaries in between. And the electrons had a volumetrical character in his model.
Here in the set of post QM times - the electrons are considered as points (just no volume and boundaries!) and in the matter is just the "vacuum" in between.
Further in p. 685 we can read that:
"Providing averaging of the Maxwell-Lorentz equations over the physically
infinitely small volume

 and time interval
and time interval

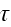 ,
we determine averaged values via
,
we determine averaged values via
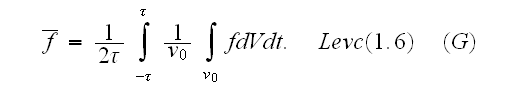
Then we have
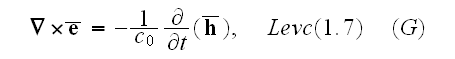
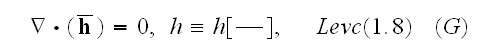
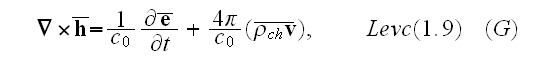
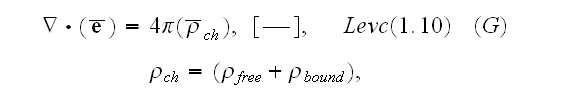
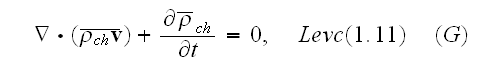
Let's introduce the following definitions
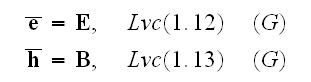
and will name the mean value of strength of electric field by strength of the
field

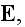 but the mean value of magnetic field strength in the medium by magnetic
induction
but the mean value of magnetic field strength in the medium by magnetic
induction

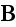 (this name of the mean magnetic field is connected exclusively to the historic
tradition)."
(this name of the mean magnetic field is connected exclusively to the historic
tradition)."
Our comments:

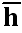 that is averaged incorrectly and declared as averaged volumetrically
that is averaged incorrectly and declared as averaged volumetrically

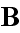 - Oh, yes, it is pretty convenient to do this!
- Oh, yes, it is pretty convenient to do this!At the same time - this is incorrect averaging. The
equality

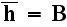 is the great streching in atomic physics.
is the great streching in atomic physics.
Because

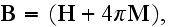 in CGSE in the already averaged induction equation; but assuming that
in CGSE in the already averaged induction equation; but assuming that

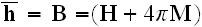 is not the same
as
is not the same
as
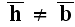 and making instantly
and making instantly

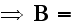

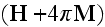 just
in the induction equation alone?! How is it by pure
averaging of this equation, let this explain to us someone with
clarity?
just
in the induction equation alone?! How is it by pure
averaging of this equation, let this explain to us someone with
clarity?
Also, there is no description on - What is the averaging volume? and
How it exactly will be averaged - if the bounding averaging volume surface is cutting through the particles, charges, atoms, molecules, etc.?
They did not need the form, shape and bounding surface of the REV, because they did not describe that REV at all!! Can we imagine this now?
And there is no correct way of saying that this surface will be moving
all the time with the closest (and not even closest?) to it particles, atoms,
etc., just to include all the previous particles within the

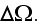
More on that - they just do the integration! In the first part of XX century they did not bother at all - how to do that averaging? They don't do averaging in most cases at all, a mean integral value, no - they do just the unspecified volume integration! That's it, no deletion on the volume of REV?! Unbelievable, but people are so accustomed to this incorrect 'averaging," that do not note - What is this mathematics all about?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Then in p. 686 (Vol. 1) one can continue to read that:
"Then, the equations (1.7) - (1.11) take forms
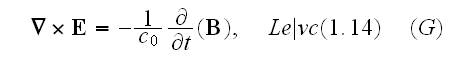
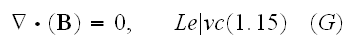
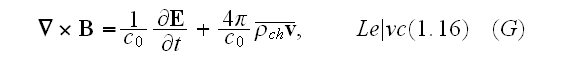
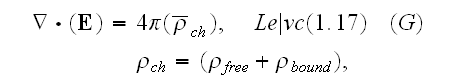
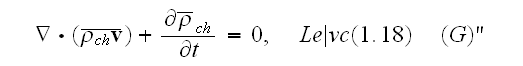
Our comments:
Also, the last equation ((1.18) should loose the

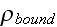 to
get to the correct (free charge flow) conservation final form. Let we see how
it can be performed in homogeneous volumeless particles atomic physics.
to
get to the correct (free charge flow) conservation final form. Let we see how
it can be performed in homogeneous volumeless particles atomic physics.
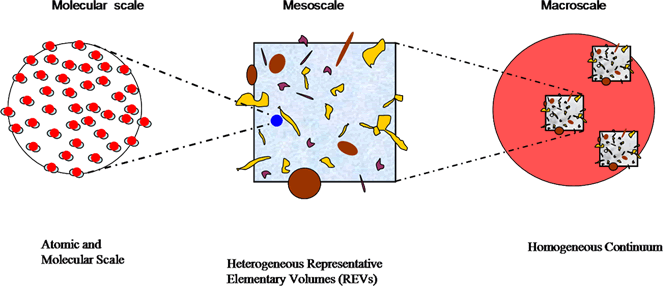
In Homogeneous physics - like in studied in this sub-section textbooks, there are no specifics, theorems to do averaging over these REVs, and even there are no definitions or wrong definitions (as in Continuum Homogeneous Mechanics) of a REV.

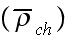 and
and

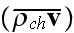 in
Atomic Scale Maxwell-Lorentz Equations
in
Atomic Scale Maxwell-Lorentz Equations
Then in pg. 686 (Vol. 1) one can continue to read that:
"Further transformation of equations is based on the finding of the mean
values of

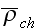 and
and

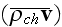 .
For finding these mean variables there are some assumptions regarding a
matter's sctructure should be made."
.
For finding these mean variables there are some assumptions regarding a
matter's sctructure should be made."
Our comments:
In p. 687 Levich starts to develop formulae for averaged charge

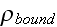 that is all physicists need to do to justify the established conventional
formulae for polarization and time dependent (transient) bound current within
the substance of interest (matter).
that is all physicists need to do to justify the established conventional
formulae for polarization and time dependent (transient) bound current within
the substance of interest (matter).
" Dipole moment, obtained by bulk substance, equal, by definition
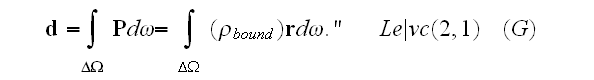
"The subscript (bound) defines that the mean charge caused by displacement of charges, that bound within atoms of a substance. This appearance of bound or induced charge named electrostatic induction or polarization.
To find out

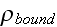 let's use the definition (2.1) and transform the integral
let's use the definition (2.1) and transform the integral

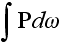 to
to

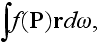 where
where

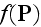 - is the some function of polarization. Then, comparing
- is the some function of polarization. Then, comparing

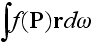 with the
with the

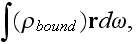 one can find
one can find

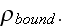 Using the formula (I,53) and denote in it
Using the formula (I,53) and denote in it

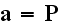 ,
,

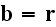 ,
find that it is used also the extension of homogeneous GO theorem as
,
find that it is used also the extension of homogeneous GO theorem as
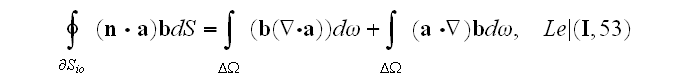
based on use of
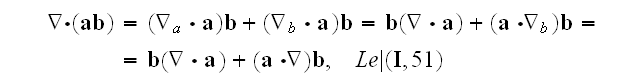
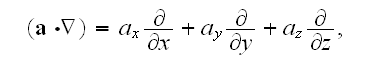
where

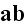 is the dyadic.
is the dyadic.
Then we can get (in Levich, 1969)
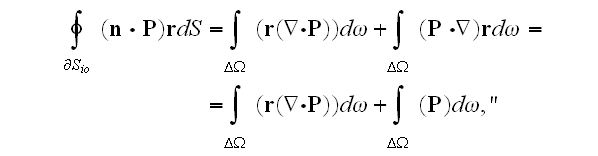
as soon as
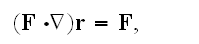
See for reference - Korn, G.A., and Korn, T.M. (1961, Russian edition) - p. 169-170.
Our comments:
We need to note that here in the above mathematics is used the
notation

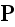 of
the polarization field as if it is
of
the polarization field as if it is

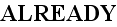

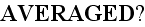 At
the Upper scale. That is - the substitution of the microscale values
(functions) under integral by the like ALREADY Averaged Macroscale
function!
At
the Upper scale. That is - the substitution of the microscale values
(functions) under integral by the like ALREADY Averaged Macroscale
function!







Then Levich (1969, V.1) writes the same trick conventional physicists did
while averaging over the unspecified REV and even for the whole body under
investigation.


He writes - "Choosing the surface of integration outside of volume occupied by body (subject matter), we have
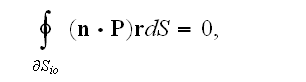
as soon as outside body polarization in equal zero."
Well, but this is the

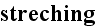 ,
,

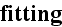 ,
and at the same time only for the bulk, the total body assessment is valid
procedure. How physicists are going to agree with this for 60-80? years? The
matter is about the "point" or the "dot" of physical matter estimation. And by
this way they suggest us to integrate over the whole body, even outside of
it?
,
and at the same time only for the bulk, the total body assessment is valid
procedure. How physicists are going to agree with this for 60-80? years? The
matter is about the "point" or the "dot" of physical matter estimation. And by
this way they suggest us to integrate over the whole body, even outside of
it?
"That is why
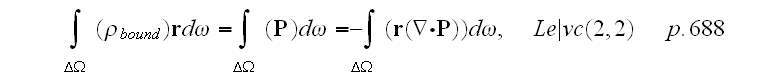
Comparing

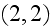 with
with

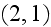
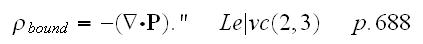
Our comments:
Meanwhile, this

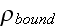 should be an averaged value! What a trick?
should be an averaged value! What a trick?
We would like to point out again - that here used the notation

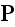 of
the polarization field as if it is
of
the polarization field as if it is

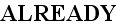

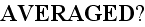 And
is at the Upper scale. That is - the substitution of the microscale values
(functions) under integral by the like ALREADY Averaged Macroscale function
And
is at the Upper scale. That is - the substitution of the microscale values
(functions) under integral by the like ALREADY Averaged Macroscale function

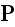 !
!

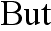






Because really should be
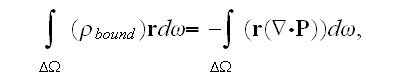
but we can not get functions out of integral sign BEFORE integration.
Nevertheless, in Levich (1969) presented the designation of the following equalities (for bound charges)
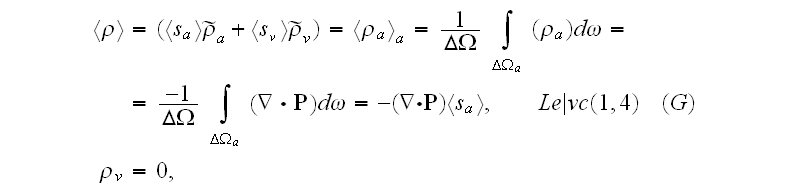
which is looks like

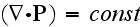 in
the domain
in
the domain

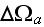 -
artificially, for this equation, then we can write
-
artificially, for this equation, then we can write
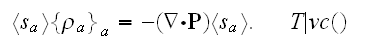
Meanwhile, even in brackets of assumed bulk outside

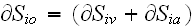 and acceptance that
and acceptance that

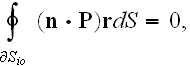 correct
will be the expression
correct
will be the expression
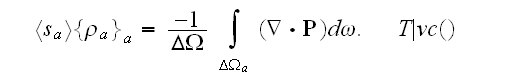

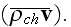
Starting in the p. 689:
"A bit more complicated is the task of calculation of the mean density of
current in the medium

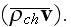 This calculation might be performed on the basis of some moleding ideas, or,
that is more formal, having general representations on electromagnetic
properties of a medium.
This calculation might be performed on the basis of some moleding ideas, or,
that is more formal, having general representations on electromagnetic
properties of a medium.
We will choose the second path, inasmuch as the models of atoms and molecules that being used usually along presentations of macroscopic electrodynamics not only far from reality,..."
Starting in the p. 690:
"The mean current density in a medium

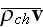 in each point of a body is the function of strength of electric and magnetic
fields. Apart of that, if these fields are changing in the space and in time,
the mean current density will depend of speed of changing of vectors
in each point of a body is the function of strength of electric and magnetic
fields. Apart of that, if these fields are changing in the space and in time,
the mean current density will depend of speed of changing of vectors

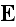 and
and

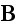 in time and of spatial derivatives of these variables, i.e.
in time and of spatial derivatives of these variables, i.e.
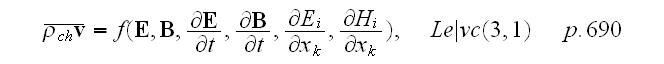
As soon as the fields apparently assumed to be weak, it is possible to expand
function

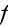 into the series over powers of the variables and restrain the expansion by the
first power terms."
into the series over powers of the variables and restrain the expansion by the
first power terms."
In the p. 691:
"Then to the accuracy of the first order terms
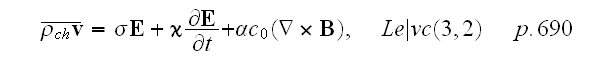
where

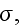

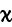 ,
and
,
and

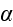 - are scalar values, dependent on the medium properties. The reason for
introduction into the last additive term the factor of light speed
- are scalar values, dependent on the medium properties. The reason for
introduction into the last additive term the factor of light speed

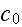 ,
will be obvious from the further text.
,
will be obvious from the further text.
The nil term in the expansion

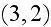 is absent, because the absence of field should correspond the current equal to
zero."
is absent, because the absence of field should correspond the current equal to
zero."
Our comments:
Author say straight in the explanations of the approach that the whole procedure and idea is of approximate nature, even the light speed is taken to fit the future substitution into the like "averaged" Amper-Maxwell law equation.
In the further derivation Levich takes course to introduce a few coefficients
and heavy use of the same unrealistic bulk assumption of surface integration
over the outside of studied piece of material (pgs. 693 in

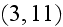 ,
694) just as of the frivolous measure to get to the needed form of final
mathematical expressions, as we respond above in comments.
,
694) just as of the frivolous measure to get to the needed form of final
mathematical expressions, as we respond above in comments.
In the p. 694:
"If the surface of integration passes outside of the volume occupied by the
body, then at this surface

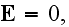 .."
.."
Then, at last, in the p. 695 one can find the resulting
expression for

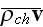 :
:
"Exploring values

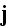 ,
,

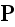 ,
,

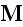 ,
the mean density of current in a substance can be finally written in the
following form
,
the mean density of current in a substance can be finally written in the
following form
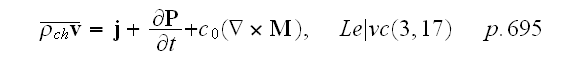
Our comments:
In a couple of pages author starts to warn reader on the domains of validity of derived in this way equations of Maxwell-Heavisde-Lorentz for a continuum mechanics applications.
In the p. 697:
"We would like to stress out that in comparison to the equations of Maxwell-Lorentz (for microscopic atomic scale electromagnetism- our note), that is among the most accurate and universal nature laws, the system of Maxwell equations has a restricted area of applicability due to limitations of domain of constitutive equations usage. "
In the p. 701:
"Let start investigation of assumptions, that were made for Maxwell equations derivation. Th emain assumption is the expansion (3.2)."
"....The more complicated is the issue applicability of expansion (3.2) in cases of high frequency and spatially-heterogeneous systems."
Our comments:
The Vlasov equation widely is known in circles of plasma physics and statistical mechanics professionals along with mathematical physics specialists.
Among many worthwhile arguments Vlasov had put forward regarding processes of collective character by physics itself, not by the theoreticians wish the few are most appealing and sound even today when researchers, people still are not getting through to the issue:
1) Theory of pair collisions formally not applicable to Coulomb interaction.
2) Theory of pair collisions is the Local events describer.
3) Long-range Coulomb interaction existence in many-many physical fields and processes (not only of plasma physics, as it is written on his intentions), is the strong reason to seek for another model, than the Boltzmann equation.
Well enough, it is known meanwhile, that Vlasov was run after even for that his arguments list above.
To this list we can add many issues, but of the only these two right now - And not only of Coulomb interaction. What about other known types of long-range collective interactions?
Another one point is that as it was written relatively recently and is not in a wide debating mode that - the Boltzmann Equation is Invalid in the Derivation. More than 100 Years of Misled Research?
The Vlasov equation can be seen as the first swallow in a series of theories, modeling schemes for a Long-Range interaction phenomena finalized with the new type of modeling equations - the integro-differential ones. In physics first of all, as well as in other sciences. This theory must be analyzed with regarding of its motivations, physical model, methods of mathematical approach and performance, and of its results so far.
Vlasov's set of equations is being presented mainly as the kinetic equation describing the behavior of a single(?) particle distribution functions of a plasma under the influence of electric and magnetic fields.
Just in case of questions - short summary is this - the Vlasov's theory and equations while are in the right direction and with good techniques, they are still of an insufficient base for a collective interaction description by physical and mathematical models.
In line with the statistical mechanics approach and equations for point-particles movement the Maxwell-Lorentz (ML) equations had been brought to the "collective self-consistent" electromagnetic fields array as the full standard set of ML equations where electric field E(r,t) and magnetic induction field B(r,t) are named as the fields of collective interaction (quasi-averaged). That form means that the Maxwell-Lorentz equations were not averaged neither in their atomic format nor in a continuum mechanics appearance. The effect of collective behavior is introduced into ML equations, model implicitly via the Vlasov equations themselves.
The techniques are still not averaging, but taking into account the collective phenomena - that we call quasi-averaging.
This piece of analysis to be continued with some mathematics.
In p. 248 Jackson (1999) starts the attempt to connect the microscale - atomic actually, and the continuum mechanics model of Maxwell-Lorentz equations, starting writing the macroscale Maxwell equations.
The discussion of electromagnetism in the preceding chapters has been based on the macroscopic Maxwell equations,
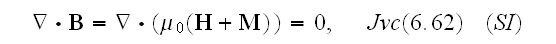
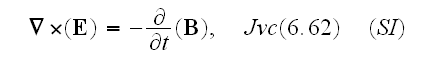
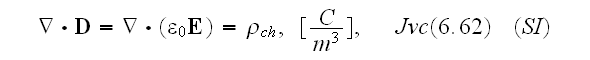
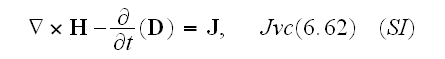
where

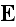 and
and

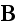 are
the macroscopic electric and magnetic field quantities,
are
the macroscopic electric and magnetic field quantities,

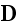 and
and

 are
corresponding derived fields, related to
are
corresponding derived fields, related to

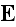 and
and

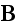 through
the polarization
through
the polarization

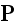 and
the magnitization
and
the magnitization

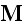 of
the material medium by
of
the material medium by
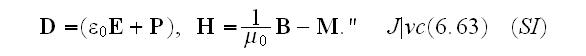
Our comments:
Which is the artificial move with regard of

 .
If one could attentively follow the further transformations of atomic scale
Maxwell-Lorentz equations to the macroscopic scale equations one would easily
locate the spot where the magnitization field
.
If one could attentively follow the further transformations of atomic scale
Maxwell-Lorentz equations to the macroscopic scale equations one would easily
locate the spot where the magnitization field

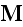 when substituted within the Ampere-Maxwell for induced magnetic field
equation
when substituted within the Ampere-Maxwell for induced magnetic field
equation
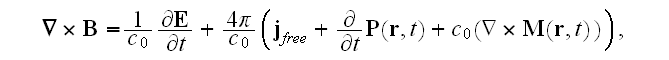
will forcibly return the formulation with

 field in the left hand side of the above equation to the original notation
with
field in the left hand side of the above equation to the original notation
with

 field that should be held just before averaging
field that should be held just before averaging
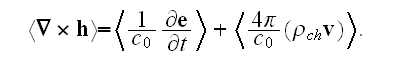
Well, it would be naturally writing that
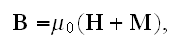
instead of

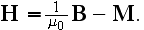
Further Jackson writes in the same page 248:
"Similarly,

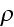 and
and

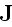 are
the macroscopic (free) charge density and current density, respectively.
Although these equations are familiar and totally acceptable, we have yet to
present a serious derivation of them from a microscopic starting point.
are
the macroscopic (free) charge density and current density, respectively.
Although these equations are familiar and totally acceptable, we have yet to
present a serious derivation of them from a microscopic starting point.
This deficiency is removed in the present section. The derivation remains within a classical framework even though atoms must be described quantum-mechanically. The excuse for this apparent inadequacy is that the quantum-mechanical discussion closely parallels the classical one,...."
"We consider a microscopic world made up of electrons and nuclei. For
dimensions large compared to

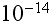

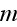 , the nuclei can be treated as point systems, as can the electrons. We assume
that the equations governing electromagnetic phenomena for these point charges
are the microscopic Maxwell equations,
, the nuclei can be treated as point systems, as can the electrons. We assume
that the equations governing electromagnetic phenomena for these point charges
are the microscopic Maxwell equations,
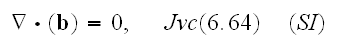
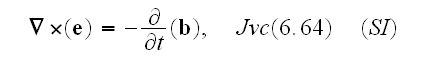
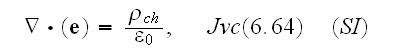
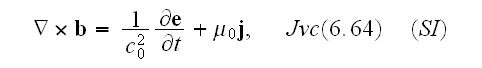
Our comments:
Well, comparing to the of really vacuum with point charges specified Maxwell-Lorentz equations as for homogenized medium, for example, these
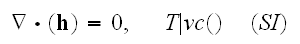
and where the Faraday law of induction equation is
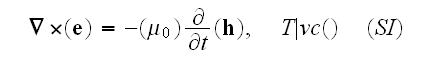

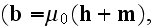

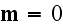 ;
;

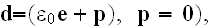
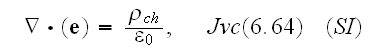
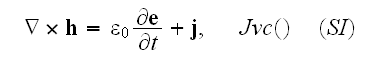
or as
above 
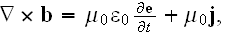

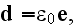



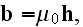
one can notice that there is difference of the three equations - first, second and the fourth.
In the Gauss law for magnetic field equation which can be written as

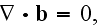 while in this and in other two equations scaling treatment dramatically change
the averaging output for a poly-"phase" atomic system, as we will sea below.
while in this and in other two equations scaling treatment dramatically change
the averaging output for a poly-"phase" atomic system, as we will sea below.
Jackson specifically hides here the real initial form of atomic scale
equations and writes equations in

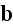 ,
,

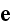 quantities (why not in al
quantities (why not in al

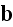 ,
,

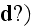 ,
not in
,
not in

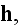

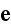 because
this would bring the pseudo-averaging done for homogeneous fields closer and
easier to the Lorentz' writing of macroscale EM equations.
because
this would bring the pseudo-averaging done for homogeneous fields closer and
easier to the Lorentz' writing of macroscale EM equations.
In p. 249 we can read the explanations for this form of microscale equations as of before averaging, specific for Homogeneous electrodynamics reasoning:
"where

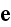 and
and

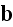 are the microscopic electric and magnetic fields and
are the microscopic electric and magnetic fields and

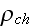 and
and

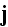 are the microscopic charge and current densities. There are no corresponding
fields
are the microscopic charge and current densities. There are no corresponding
fields

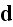 and
and

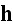 because all the charges are included in
because all the charges are included in

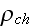 and
and

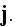 "
"
Our comments:
What if the charges are included into equations (3) and (4)?
The charge presence is not a justification or reason for substitution of averaging mathematics; the charges are included because the particles are artificial - meaning the particles are smeared all over the volume.

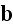 unless we either making a "SPECIAL" theory related to a separate particle
(electron, nucleus) and only, or have been averaged the field over the some
specified volume (that would include the "vacuum" and the particles, but not a
homogenized unknown one "phase" which is called vacuum (and which is the mix
of "vacuum" and of smeared particles presented as volumeless "dot-points") -
as of an atom or of larger dimension as the REV and have already received that
field
unless we either making a "SPECIAL" theory related to a separate particle
(electron, nucleus) and only, or have been averaged the field over the some
specified volume (that would include the "vacuum" and the particles, but not a
homogenized unknown one "phase" which is called vacuum (and which is the mix
of "vacuum" and of smeared particles presented as volumeless "dot-points") -
as of an atom or of larger dimension as the REV and have already received that
field

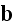 as a result of averaging with all components of this
as a result of averaging with all components of this

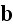 field,
but obtained as by averaging and shown as averaged either over the atom or the REV.
field,
but obtained as by averaging and shown as averaged either over the atom or the REV.
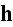 with
with

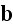 is just the "fixing" to the Lorentz form of continuum scale equations.
is just the "fixing" to the Lorentz form of continuum scale equations.
Also, why not having the same substitution with regard of the

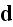 ?
Because anyway there is no polarization
?
Because anyway there is no polarization

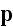 field so far in the equation?
field so far in the equation?
Well, the same should be said and about

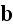 -
there is no still magnetization in the equations at atomic scale, right? Why
to change
-
there is no still magnetization in the equations at atomic scale, right? Why
to change

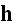 with
with

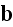 in this case?
in this case?
Further in p. 249 we can read:
"A macroscopic amount of matter at rest contains of the order of

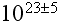 electrons and nuclei, all in incessant motion because of thermal agitation,
zero point vibration, or orbital motion. The microscopic electromagnetic
fields produced by these charges vary extremely rapidly in space and in time.
electrons and nuclei, all in incessant motion because of thermal agitation,
zero point vibration, or orbital motion. The microscopic electromagnetic
fields produced by these charges vary extremely rapidly in space and in time.
The spatial variationsoccur over distances of the order of

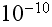 or less, and the temporal fluctuations occur with periods ranging from
or less, and the temporal fluctuations occur with periods ranging from

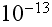

![$[s]$](DownM-L-203__242.png) for nuclear vibrations to
for nuclear vibrations to

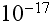

![$[s]$](DownM-L-203__244.png) for
electronic orbital motion. Macroscopic measuring devices generally average
over intervals in space and time much larger that these.
for
electronic orbital motion. Macroscopic measuring devices generally average
over intervals in space and time much larger that these.
All the microscopic fluctuations are therefore averaged out, giving relatively smooth and slowly varying macroscopic quantities, such as appear in the macroscopic Maxwell equations."
Further in p. 249 we can read:
"The question of what type of averaging is appropriate must be examined with some care. At first glance one might think averages over both space and time are necessary. But this is not true. Only a spatial averaging is necessary.
(Parenthetically, we note that a time averaging alone would certainly not be sufficient, as can be seen by considering an ionic crystal whose ions have small zero point vibrations around well-defined and separated lattice sites.)
To delimit the domain where we expect a macroscopic description of
electromagnetic phenomena to work, we observe that the reflection and
refraction of visible light are adequately described by the Maxwell equations
with a continuous dielectric constant, where as x-ray diffraction clearly
exposes the atomistic nature of matter. It is plausible therefore to take the
length

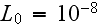

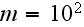 Å as the absolute lower limit to the macroscopic domain.
Å as the absolute lower limit to the macroscopic domain.
The period of oscillation associated with light of this wavelength is

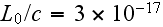 s. In a volume of
s. In a volume of

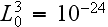

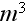 there are, in ordinary matter, still of the order of
there are, in ordinary matter, still of the order of

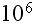 nuclei and electrons. Thus in any region of macroscopic interest with
nuclei and electrons. Thus in any region of macroscopic interest with

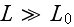 there are so many nuclei and electrons that the fluctuations will be
completely washed out by a spatial averaging.
there are so many nuclei and electrons that the fluctuations will be
completely washed out by a spatial averaging.
On the other hand, because the time scale associated with is actually in the range of atomic and molecular motions, a time-averaging would not be appropriate. There is, nevertheless, no evidence after the spatial averaging of the microscopic time fluctuations of the medium."
Our comments:
Well, we can comment with assessments for close by the sub-volumes REVs for continuum media averaging.
If in a REV

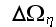 we have
we have

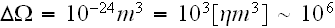

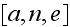 then in REV
then in REV

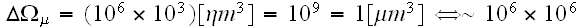

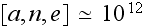

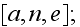
then in a REV

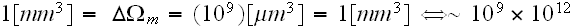

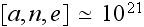

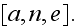
That is, in all these two macroscale REVs simulated above - of

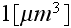 and of
and of

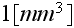 there are tremendous number of particles, atoms, small molecules.
there are tremendous number of particles, atoms, small molecules.
In p. 249 we can observe the firstly introduced the concept of averaging in Homogeneous electrodynamics:
"The spatial average of function

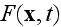 with respect to a test function
with respect to a test function

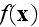 is defined as
is defined as
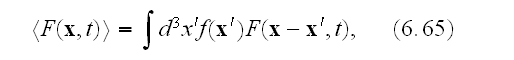
where

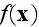 is real, nonzero in some neighborhood of
is real, nonzero in some neighborhood of

 and normalized to unity over all space. It is simplest, though not necessary,
to imagine
and normalized to unity over all space. It is simplest, though not necessary,
to imagine

 to be nonnegative. To preserve without bias directional characteristics of
averaged physical properties, we make
to be nonnegative. To preserve without bias directional characteristics of
averaged physical properties, we make

 isotropic in space. Two examples are
isotropic in space. Two examples are
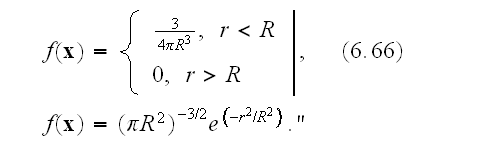
In p. 250 we can observe
"Since space and time derivatives enter the Maxwell equations, we must consider these operations with respect to averaging according to (6.65). Evidently, we have
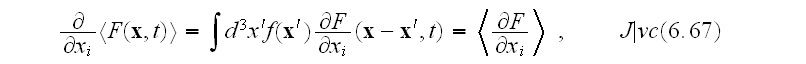
and
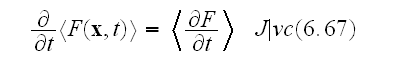
The operations of space and time differentiation thus commute with the averaging operation."
Our comments:
We ought to declare the complete ignorance also and of this rather well known author regarding the averaging mathematics as it was developed since 1967.
1) The first is that the real averaging volume - Representative Elementary
Volume (REV) has never been described or even briefly illustrated
in homogeneous physics.
Even there is no figure that students can locate in textbooks (if anyone find and point me out the place of publication, I will comment on that).
And this is common in orthodox homogeneous physics - researcher, reader or student can be easily driven into a variable false constructions in need at any moment. Mostly in atomic and particle physics this is the frivolous REV - most often the REV that is so large that it embraces the whole subject, piece of matter, material that is under investigation. This is done to declare many surficial integrals equal to zero.
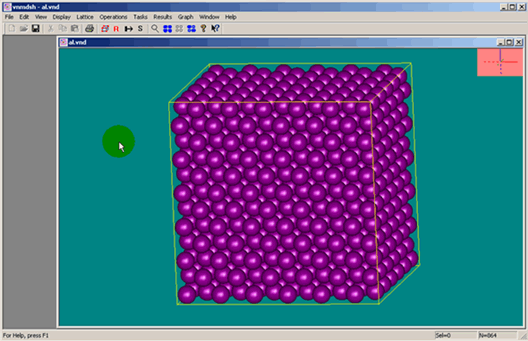
Figure 2: A computer generated picture of simulation Volume at molecular scale with the rigid for data reduction bounding surfaces. No one commercial software package can do the HSVAT for Heterogeneous and Atomic scale simulation.

 and
and

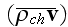 at the end needs to be fixed (fitted) the mathematical expressions for
surficial integral in a way that nullify the very important terms that we need
to retain for correct integration.
at the end needs to be fixed (fitted) the mathematical expressions for
surficial integral in a way that nullify the very important terms that we need
to retain for correct integration.
2) The formulae

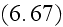 hide the important features of averaging for multiphase heterogeneous media.
hide the important features of averaging for multiphase heterogeneous media.
And they have been falsified anyway, because the correct physical and mathematical methods of HSP-VAT already have proved for many problems that homogeneous methods just bring approximate and often misleading incorrect results..
The thing is that the averaging for heterogeneous and scaled matter is the quite different operations comparing to what was accepted at the edge of XX century in physics and math, see basics in our -
and in
At the same time - it would be useful to remind here in more detail what is in many sciences including homogeneous electrodynamics understood under the term "averaging."
It is just
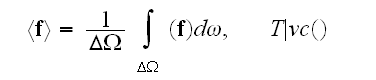
for whatever function or operator one might has.
Meanwhile, if the medium consists of at least two constituents then we need to
derive the REV averaged function over

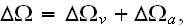 for example, by integration
for example, by integration
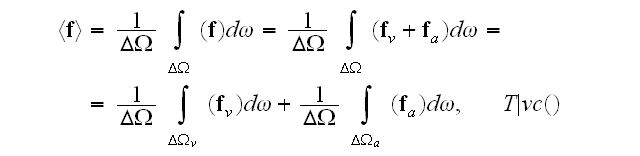
with the all heterogeneous, scaled consequences of that for derivatives, operators, and equations.
Further in p. 250 we can observe:
"We can now consider the averaging of the microscopic Maxwell equations
(6.64). The macroscopic electric and magnetic field
quantities

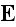 and
and

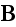 are defined as the averages of the microscopic fields
are defined as the averages of the microscopic fields

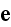 and
and

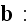
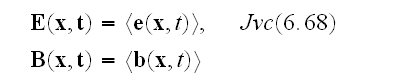
Then the averages of the two homogeneous equations in (6.64) become the corresponding macroscopic equations,
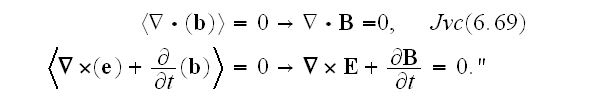
Our comments:

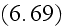 are the wrong averaging expressions and equations for our polyphase media in
the REV.
are the wrong averaging expressions and equations for our polyphase media in
the REV.
In p. 251 we can continue to observe the path with which author tries to pseudo-average the other two microscale equations:
"The averaged inhomogeneous equations from (6.64) become
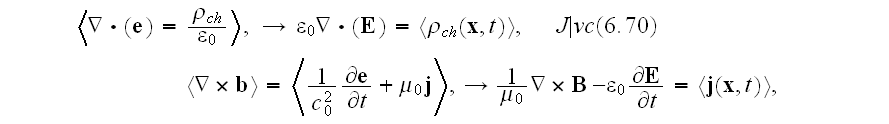
Comparison with the inhomogeneous pair of macroscopic equations in

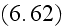 indicates
the already known fact that the derived fields
indicates
the already known fact that the derived fields

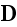 and
and

 are introduced by the extraction from
are introduced by the extraction from

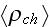 and
and

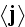 of certain contributions that can be identified with the bulk properties of
the medium. The examination of
of certain contributions that can be identified with the bulk properties of
the medium. The examination of

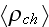 and
and

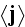 is therefore the next task."
is therefore the next task."
Our comments:
We are witnessing a trick in this path - first in

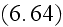 there
were just the substitution of
there
were just the substitution of

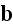 instead of
instead of

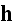 ,
then now in
,
then now in

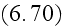 the
same like "averaged" quantity
the
same like "averaged" quantity

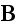 get back substituted to
get back substituted to

 in the following one-two steps in derivation, while the pseudo-averaged
in the following one-two steps in derivation, while the pseudo-averaged

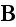 is declared as that it is in the final "averaged" equations the quantity
is declared as that it is in the final "averaged" equations the quantity

 will appear to be the "derived" field, along with the
will appear to be the "derived" field, along with the

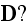
In the textbook by Schwinger et al. (1998) given the good example of reasoning, methods used in homogeneous physics to derive (and by this to validate, justify) the Maxwell-Lorentz electrodynamics equations for a continuum. Everyone was able to analyze these rather complicated mathematically ideas and methods used for "homogenized" mixing of atomic scale particles and of the "vacuum" to get Up to the continuum media electromagnetism governing equations.
We would extend our consideration of this theory in the pairing sub-section -
where the contribution to the multi"phase" Scaleportation theory for electrodynamics equations, models between atomic and continuum descriptions have been worked out.
Finally authors bring all the formulae working for the idea to get the Lorentz averaged electrodynamics equations.
In p. 42:
" The final form of the historical, macroscopic Maxwell equations is
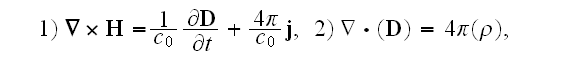
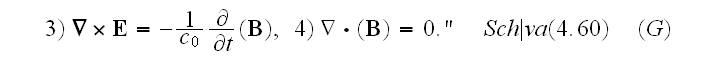
We are approaching this interesting and deep text on atomic to continuum mechanics Maxwell-Lorentz transformation basics with the open and adverse analysis in our accompanying sub-section -
One can read from the abstract of Mills (2003) paper:
"Despite its successes, quantum mechanics (QM) has remained mysterious to all who have encountered it. Starting with Bohr and progressing into the present, the departure from intuitive, physical reality has widened. The connection between QM and reality is more than just a "philosophical" issue. It reveals that QM is not a correct or complete theory of the physical world and that inescapable internal inconsistencies and incongruities arise when attempts are made to treat it as physical as opposed to a purely mathematical "tool.""
"In an attempt to provide some physical insight into atomic problems and
starting with the same essential physics as Bohr of

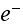 moving in the Coulombic field of the proton and the wave equation as modified
by Schrodinger, a classical approach is explored that yields a
remarkably accurate model and provides insight into physics on the atomic
level."
moving in the Coulombic field of the proton and the wave equation as modified
by Schrodinger, a classical approach is explored that yields a
remarkably accurate model and provides insight into physics on the atomic
level."
"Physical laws and intuition may be restored when dealing with the wave
equation and quantum-mechanical problems. Specifically, a theory of classical
quantum mechanics (CQM) is derived from first principles that successfully
applies physical laws on all scales. Rather than using the postulated
Schrodinger boundary condition "

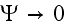 as r
as r

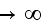 ,"
which leads to a purely mathematical model of the electron, the constraint is
based on experimental observation. Using Maxwell's equations, the classical
wave equation is solved with the constraint that the bound (n = 1)-state
electron cannot radiate energy."
,"
which leads to a purely mathematical model of the electron, the constraint is
based on experimental observation. Using Maxwell's equations, the classical
wave equation is solved with the constraint that the bound (n = 1)-state
electron cannot radiate energy."
Our comments:
Many good things are versed here in the abstract. The promise is great.
"The result gives a natural relationship among Maxwell's equations, special relativity, and general relativity. CQM holds over a scale of space-time of 85 orders of magnitude --- it correctly predicts the nature of the universe from the scale of the quarks to that of the cosmos."
Our comments:
That is seemed of too much of scales and of too much of physics included within these scales to make this connection all happens. Also, and the main drawback of this statement, that the different scales physics, objects, phenomena are of heterogeneous nature - so, it can not be described with the OSFA (One Scale For All) governing, modeling equations.
About 85 orders of magnitudes it is an excessive claim.
In p. 436 author writes on peculiarities of atomic physics:
"2. CLASSICAL QUANTUM THEORY OF THE ATOM BASED ON MAXWELL'S EQUATIONS THAT HOLDS OVER ALL SCALES
In this paper the old view that the electron is a zero or one-dimensional point
in an all-space probability wave-function Y(x) is not taken for granted. The
theory of CQM, derived from first principles, must successfully and
consistently apply physical laws on all
scales.
 Historically, the point at which QM broke with classical laws can be traced to
the issue of nonradiation of the one-electron atom that was addressed by Bohr
with a postulate of stable orbits in defiance of the physics represented by
Maxwell's
equations.
Historically, the point at which QM broke with classical laws can be traced to
the issue of nonradiation of the one-electron atom that was addressed by Bohr
with a postulate of stable orbits in defiance of the physics represented by
Maxwell's
equations.
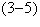
Later, physics was replaced by "pure mathematics" based on the notion of the inexplicable wave-particle duality nature of electrons, which lead to the Schrodinger equation, where the consequences of radiation predicted by Maxwell's equations were ignored. Ironically, both Bohr and Schrodinger used the electrostatic Coulomb potential of Maxwell's equations but abandoned the electrodynamic laws."
In p. 437 author continues:
"The mass energy and angular momentum of the electron are constant; this requires that the equation of motion of the electron be temporally and spatially harmonic. Thus the classical wave equation applies and
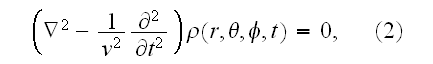
where

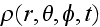 is the time-dependent charge density function of the electron in time and
space. In general, the wave equation has an infinite number of solutions. To
arrive at the solution that represents the electron a suitable boundary
condition must be imposed. It is well known from experiments that each single
atomic electron of a given isotope radiates to the same stable state. Thus the
physical boundary condition of nonradiation of the bound electron was imposed
on the solution of the wave equation for the time-dependent charge density
function of the
electron.
is the time-dependent charge density function of the electron in time and
space. In general, the wave equation has an infinite number of solutions. To
arrive at the solution that represents the electron a suitable boundary
condition must be imposed. It is well known from experiments that each single
atomic electron of a given isotope radiates to the same stable state. Thus the
physical boundary condition of nonradiation of the bound electron was imposed
on the solution of the wave equation for the time-dependent charge density
function of the
electron.
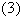 The condition for radiation by a moving point charge given by
Haus
The condition for radiation by a moving point charge given by
Haus
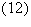 is that its space-time Fourier transform possess components that are
synchronous with waves traveling at the speed of light."
is that its space-time Fourier transform possess components that are
synchronous with waves traveling at the speed of light."
"Conversely, it is proposed that the condition for nonradiation by an ensemble of moving point charges that makes up a current density function is as follows: For nonradiative states, the current density function must not possess space-time Fourier components that are synchronous with waves traveling at the speed of light."
"Thus an electron is a spinning, two-dimensional spherical surface (zero thickness1), called an electron orbitsphere, that can exist in a bound state at only specified distances from the nucleus, as shown in Fig. 1. The corresponding current function shown in Fig. 2, which gives rise to the phenomenon of spin, is derived in Section 4."
Our comments:
No matter what is in the CQM theory is right and what is wrong, the acute issues, questions raised by other interested physicists, mathematicians should be either overthrown or explained. In line with critics from participants of http://tech.groups.yahoo.com/group/hydrino/message/11316
this is a partial list of serious questions toward the theory of CQM:
1. The claimed function f(r) for the radial component of the solution to the wave equation does not satisfy the differential equation.
2. The computation of the orbitsphere radius is wrong, with the consequence that the computation of the potential energy is also wrong.
3. The computation of angular kinetic energy is wrong.
4. The two computations of angular momentum are both wrong.
5. The computed energy of trapped photons is wrong.
6. The computation of mass/charge density of the orbitsphere
is wrong.
7. The computed moment of inertia is wrong.
8. There is no coherent explanation for resonant transfers of energy.
9. The 'free' electron configuration is not a solution to the 'wave equation'.
10. The computations of spectral lines are done incorrectly.
Our further comments:
The number of issues in CQM also are of serious value for understanding of physical realities, not modeled with SQM, or modeled without connection to reality.
Among them what is welcomed have a long rather list of things that describe at least the attempts to model phenomena with the nature recognized tools. We would enumerate some as:
1) The claim to present particles, at least electron, photon as the objects in 3D space with behavior partially, at least, complied with the Maxwell-Lorentz modeling equations. There are issues remained about an orbitsphere and other.
2) The attempts to describe phenomena with help of classical deterministic tools. It is known that the deterministic picture of the events, phenomena in physics or elsewhere always are in change of statistical (statistical mechanics) methods when the amount of knowledge about that phenomena of objects is accumulated above the certain level when it is preferable or even obligatory to turn to more elucidative and accurate deterministic (causal) methods, tools.
1) The presentation of particles still as the point objects.
This contradicts to the idea of particles as the physical objects - the points are not the physical objects. Those are just the points with the assigned BY US PROPERTIES.
2) Directly related to the above is the issue of using the Maxwell-Lorentz equations for modeling of the POINTS?
3) The attempts to deal with the collective behavior of electrons, other particles in a surrounding media as things that could be described as at the same scale and with the homogeneous theoretical approach.
1) All the effort spent by physicists in XX century when for justifying the appearance of Maxwell-Heaviside-Lorentz electrodynamics continuum scales equations was to find out the appropriate or approximate mathematical procedures which can be called "fixing" for making way to pseudo-average the atomic scale Lorentz electromagnetism equations and present them looking as the macroscale equations also by Lorentz, but for which Lorentz could not use the correct averaging (scaled) mathematics and physics that appeared at the end of XX century.
Up to now physicists had not used the correct scaled averaging methods for atomic scale Maxwell-Heaviside-Lorentz electrodynamics equations.
2) Because the problem of averaging of the array of moving atoms, molecules, free electrons embedded in a medium that can be called vacuum (and is not really empty space) is the problem of scaled heterogeneous physics, it should be treated with the tools of that physics including first of all the various Volume-Surface integration theorems, developed for Heterogeneous media.
That is why the methods used in homogeneous physics must fail and have been failing for >130 years to develop the correct macroscale medium electrodynamics governing equations.
3) What is used right now in physics as the macroscale continuum medium, even homogeneous, Maxwell-Heaviside-Lorentz electrodynamics equations is the statement that adjusted (and we have shown how it is usually done) to the form developed by Lorentz and that is the incomplete governing equations set for electromagnetism phenomena.
4) Generally, these averaging formulae and pseudo-averaged EM governing equations used up to now in homogeneous microscale electrodynamics, are not correct for atomic scale, for the Upper scales averaging, for Heterogeneous media. That is why the orthodox conventional physics for so many years since 1967 and during the following in the 80-90s developments in the HSP-VAT tried to ignore, suppress and silence the truthful physics and mathematics of multiphase microscale electrodynamics theory, modeling with averaging and scaleportation, presented in the HSP-VAT methods and math.
Because of this way of homogeneous averaging in atomic and particle physics as given above for averaging of Maxwell-Heaviside-Lorentz equations, the Upper scale (continuum mechanics) equations have been falsified and incomplete.
5) Lorentz himself in his "Clerk Maxwell's Electromagnetic Theory. The Rede Lecture for 1923, Cambridge" (1923) used to say that:
"Will it be possible to maintain these equations? I am not thinking here of the comparatively slight modifications that have been necessary in the theory of relativity;.....
A greater and really serious danger is threatening from the side of the quantum theory, for the existence of amounts of energy that remain concentrated in small spaces during their propagation, to which several phenomena seem to point, is in absolute contradiction to Maxwell's equations.
However this may be, even if further development should require profound alterations, Maxwell's theory will always remain a step of the highest importance in the progress of physics."
6) There would be many formulations in electrodynamics for different matters and for different scales. Not as of the case that used right now which is the application of the same kind of Lorentz' Continuum Mechanics electrodynamics equations for any scale and any medium. Just using changed coefficients that are the adjusting parameters right now.
7) We have found the ways to obtain the Upper macroscale of Continuum Mechanics modeling electrodynamics equations all based on correct heterogeneous mathematics applied to the atomic scale Equations of Maxwell-Heaviside-Lorentz -
Hecht, L., "SHOULD THE LAW OF GRAVITY BE REPEALED? The Suppressed Electrodynamics of Ampere-Gauss-Weber," Editorial, 21st Century Science & Technology, Spring, (2001)
Hecht, L., "Science: To Be, or Not to Be Or, How I Discovered the Swindle of Special Relativity," Editorial, 21st Century Science & Technology, Winter 1999-2000, (2000)
Hecht, L., "The Atomic Science Textbooks Don't Teach. The Significance of the 1845 Gauss-Weber Correspondence," Editorial, 21st Century Science & Technology, pp. 21-43, (1996)
Jackson, J., Classical Electrodynamics, 3rd ed., Wiley and Sons, New York, NY, (1999). pp. 1-808.
Landau, L.D. and Lifshits, E.M., Electrodynamics of Continuous Media, Pergamon Press, Oxford, (1960).
Landau, L.D. and Lifshits, E.M., Electrodynamics of Continuous Media, Gos. Izd. Tekh.-Teor. Lit., Moscow, (1957). 532 pgs. (in Russian).
Levich, V.G., Course of Theoretical Physics, Vol. 1, Nauka Publishing, Moscow, (1969). (in Russian). 912 p.
Lorentz, H.A., The Theory of Electrons and Its Applications to the Phenomena of Light and Radiant Heat : a Course of Lectures Delivered in Columbia University in 1906, Dover, New York, N.Y., (1952). pp. 1-343.
Lorentz, Hendrik A., Clerk Maxwell's Electromagnetic Theory. The Rede Lecture for 1923,Cambridge University Press, Cambridge, (1923). pp. 1-35.
Maxwell, J.C., A Treatise on Electricity and Magnetism, Vol. 1, 3rd Ed., Oxford University Press, New York, (2002a). pp. 1-506, plus 14 pages with the figures attached.
Maxwell, J.C., A Treatise on Electricity and Magnetism, Vol. 2, 3rd Ed., Oxford University Press, New York, (2002b). pp. 1-500, plus 6 pages with the figures attached.
Mills, R.L., "Classical Quantum Mechanics," Physics Essays, Vol. 16, No. 4, pp. 433-498, (2003)
Mills, R.L., "Maxwell's Equations and QED: Which is Fact and Which is Fiction,"
Mills, R. L., "The Fallacy of Feynman's Argument on the Stability of the Hydrogen Atom According to Quantum Mechanics," submitted; posted at http://www.blacklightpower.com/theory/theorypapers/Fallacy_Feynmans_Argument_030705.pdf.
Purcell, E.M., Electricity and Magnetism, Berkeley Physics Course, Vol. 2, Nauka, Moscow, (1971). 448 p. (in Russian)
Schwinger, J., DeRaad, L.L.Jr., Milton, K.A., and Tsai, W-y., Classical Electrodynamics, Perseus Books, Reading, Massachusetts, (1998). 569p.
Smith, G.S., An Introduction to Classical Electromagnetic Radiation, Oxford University Press, New York, (1997). pp. 1-653.
Vinogradov, A.P., Electrodynamics of Composite Materials, Moscow, Aditorial URSS, (2001). 208 p.
Vlasov, A.A., "On Vibration Properties of Electron Gas," J. Exp. Theor. Phys., Vol. 8, No. 3, pp. 291-, (1938). (in Russian).
Vlasov, A.A., "The Vibrational Properties of an Electron Gas," Soviet Physics Uspekhi, No. 10, pp. 721- , (1968).
Vlasov, A.A., "On the Kinetic Theory of an Assembly of Particles with Collective Interaction," Journal of Physics USSR, Vol. 9, No. 1, pp. 25 - 40, (1945).
Vlasov, A.A., "On the Theory of the Solid State," Journal of Physics USSR, Vol. 9, No. 2, pp. 130--138, (1945).
Vlasov, A.A., Many-Particle Theory and Its Application to Plasma, Gordon and Breach, New York, (1961).
5) Travkin, V.S., Catton, I., and Ponomarenko, A.T., "Three Scale Hierarchical Modeling of Electrostatics and Electrodynamics in Porous Ferrites; Effective Dielectric Properties and Experiments," in Proc. 5th IUMRS-Int. Conf. Advansed Materials'99, Beijing, Vol. 2, p. 684, (1999a)
7) Travkin, V.S., and I. Catton, "Radiation Heat Transport in Porous Media," in Proc. ASME, HTD-364-3, Vol. 3, pp. 31-40, (1999)
8) Travkin, V.S., I. Catton, K. Hu, A.T. Ponomarenko, and V.G. Shevchenko, (1999), "Transport Phenomena in Heterogeneous Media: Experimental Data Reduction and Analysis", in Proc. ASME, AMD-233, Vol. 233, pp. 21-31, (1999b)
9) Ponomarenko, A.T., Ryvkina, N.G., Kazantseva, N.E., Tchmutin, I.A., Shevchenko, V.G., Catton, I.,and Travkin, V.S., "Modeling of Electrodynamic Properties Control in Liquid-Impregnated Porous Ferrite Media", in Proc. SPIE Smart Structures and Materials 1999, Mathematics and Control in Smart Structures, V.V. Varadan, ed., Vol. 3667, pp. 785-796, (1999c)
10) Travkin, V.S., Catton, I., Ponomarenko, A.T., Gridnev, S.A., Kalinin, Yu.E., Darinskiy, B.M., (2000), "Electrodynamics and Electrostatics in Heterogeneous Media. Effective Properties and their Assessments," in Proc. PIERS'2000: Progress in Electromagnetics Res. Symp., p. 1028, (2000a)
11) Travkin, V.S., Catton, I., Ponomarenko, A.T., Gridnev, S.A., Kalinin, Yu.E., Darinskiy, B.M., (2000), "Ferromagnetism in Scaled Hierarchical Materials. Wave Absorption on Micro- and Macroscale," in Proc. PIERS'2000: Progress in Electromagnetics Res. Symp., p. 1029, (2000b)
12) Travkin, V.S. and Catton, I.., "Transport Phenomena in Heterogeneous Media Based on Volume Averaging Theory", Advances in Heat Transfer, Vol. 34, pp. 1-144, (2001a)
13) Ponomarenko, A.T., Shevchenko, V.G., Ryvkina, N.G., Chmureva, V.V., Tchmutin, I.A., and Travkin, V.S., "Electrical Transport and Relaxation Processes in Polymeric Materials: Modeling and Experimental Results", Condensed Matter and Interfaces, Vol. 3, No. 1, pp.73-81 (in Russian), (2001)
14) Travkin, V.S. and Catton, I., "Heat and Charge Conductivities in Superlattices - Two-Scale Measuring and Modeling," in Proc. Intern. Mech. Engin. Congress and Exposition (IMECE'2001), IMECE/HTD-24260, pp.1-12, (2001b)
15) Travkin, V.S. and Catton, I., "Analysis of Measuring Techniques for Superlattices Thermal Conductivity Measurements," in Proc. Intern. Mech. Engin. Congress and Exposition (IMECE'2001), IMECE/HTD-24348, pp.1-12, (2001c)
16) Travkin, V.S., Catton, I., Ponomarenko, A.T., and Kalinin, Yu.E., "Bottom Up and Top Down, from Nano-Scale to Micro-Scale, Hierarchical Descriptions of Electrodynamic, Thermal and Magnetic Fields in Ferromagnets and HTSCs", in Proc. DOE 20th Symposium on Energy Engineering Sciences, Argonne National Laboratory, pp. 296-304, (2002)
17) Travkin, V. S. and Ponomarenko, A. T., "Electrodynamic Equations for Heterogeneous Media and Structures on the Length Scales of Their Constituents", Inorganic Materials, Vol. 40, Suppl. 2, pp. S128 - S144, (2004)
18) Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications -1," Journal of Alternative Energy and Ecology, No. 3, pp. 7-17, (2005a)
19) Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 2," Journal of Alternative Energy and Ecology, No. 4, pp. 9-22, (2005b)
20) Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 3," Journal of Alternative Energy and Ecology, No. 5, pp. 34-44, (2005c)
![]()

![]()