The main differences are due to different Heterogeneous mathematics and naturally governing equations for the UPPER scale physics description. These equations are mainly different because the Heterogeneous Whitaker-Slattery-Anderson-Marle (WSAM) kind of theorems applied to problem's formulation bring out equations with few (many) additional, often nonlinear terms.
| Cross-Section of Phase #1 on the Bounding Surface | |
 | |
| Homogeneous Gauss-Ostrogradsky Theorems | Heterogeneous WSAM Whitaker-Slattery-Anderson-Marle "Gauss-Ostrogradsky" Theorems |
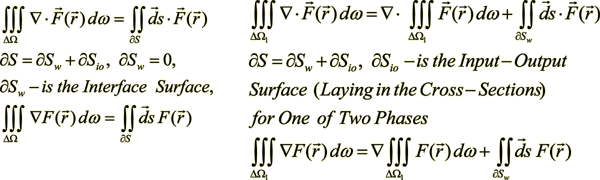 | |
The Difference is in the Additional Differential and Integral Terms in the Right Hand Side of Equalities for Heterogeneous Theorems and Governing Equations
Later efforts in 70s-90s (see among others including ours, the great publications by Gray, et al., 1993; Gray and Hassanizadeh, 1989) brought in the substantial number of various averaging HSP-VAT theorems for 1D - 3D cases.
The Detailed Micro-Modeling - Direct Numerical Modeling (DMM-DNM) method used predominantly now as the most "full and correct" method for Upper scale models, is mostly incorrect for this purpose. Especially, when the effective properties and the upper scale characteristics sought as the calculated ones based on these Lower Scale model's solution fields or when compared with experiment or sought to be used for experimental basics.
The DMM-DNM is good for the Lower scale, but averaging and other operations for and over the Upper scale functions, operators, etc. done with the Homogeneous GO theorem are mostly wrong.
On the other hand, we would like to state again and again that the Homogeneous subject physics is just the genuine constituent part of the broader business of the Heterogeneous description of matter. And there is no contradiction in this statement.
What physics was and is using for the Homogeneous matter - on this or that particular scale, is the internal part of the next Upper or the outer part of the preceding Lower scale of the substance described. This is nobody seems object to! But when the connection, interaction between the scales are in need to be assessed precisely and definitely, then the conventional contemporary "Homogeneous" physics has failed so far to address the issue.
INTRODUCTION
The formulation of heterogeneous medium transport equations has evolved a great deal since the 1950-s. Even so, the proper form of the governing equations for a heterogeneous (including porous) media is still a source of frequent discord.
Determination of the flow-variables and the magnitude of the scalar fields transport for problems involving heterogeneous porous media is difficult, even when subject to simplifications allowing specification of the medium periodicity or regularity. Linear or linearized models fail to intrinsically account for transport phenomena, requiring dynamic coefficient models to correct for short-comings in the governing models. Additionally, when attempting to describe processes in a heterogeneous media the correct form of the governing equations remains an area of debate among various researchers (see, for example, Whitaker, [7, 8, 9, 10]; Koch and Brady, [11]; Travkin, [1-3,16-27]; Travkin and Bolotina, [6]; Travkin and Catton, [4,5]). Allowing inhomogeneities to be of random or stochastic character further compounds the already daunting task of properly identifying pertinent transport mechanisms and predicting transport phenomena.
Mathematical simulation of physical processes in a highly non-homogeneous media, in general, calls for obtaining averaged characteristics of the medium and, consequently, the averaged equations. Those equations would be of the Upper spatial scale. The averaging of processes in a randomly organized media can be performed with different levels of rigorousness. If a physical model has several interdependent structurally organized levels of processes underway, it is expedient to employ one of the hierarchical methods of simulation ( for example, see Kheifets and Neimark [12], and Cushman [13] among others). The hierarchical principle of simulation consists of successively studying the processes at a number of structural levels.
One first deals with the smallest scale element, for example a small smooth capillary or globular media. Next, various types of capillary wall morphology are incorporated. This is followed by studies of a range of diameters, first smooth then rough, and then networking. Regular variations of the parameters are treated first, followed by random. This is done at each level. This approach is used for capillary morphologies as well as for granular or other morphologies in Continuum Media sciences. Meanwhile, the same physical and mathematical challenges are at the first place at any scale physics - Continuum Mechanics, Nano-scales, or/and Sub-atomic scales physical sciences.
The process leads one to find ways to deal with the large number of closure expressions that result from the Volume Averaging Theory (VAT) used to obtain the original governing set of equations for Upper scale. Although of a common form, the resulting usable form depends on the media morphology and the local boundary conditions at the each level of the hierarchy. A particular closure expressions will be different for energy, mass or momentum transfer between the fluid and the solid matrix in a porous media, between the one phase of the Heterogeneous medium and another (or others) phase in part because of their different boundary conditions, while in part due to different physics phenomena being investigated Travkin, [1-3,16-27]; Travkin and Bolotina, [6]; Travkin and Catton, [4,5].
There are many disagreements about the applicability of models based on conventional diffusivity type models of transport phenomena in Heterogeneous (and porous) media to media with the following features: 1) multi-scaled media; 2) media with non-linear physical characteristics; 3) polydisperse morphologies; 4) materials with phase anisotropy; 5) media with non-constant or field dependent phase properties; 6) transient problems; 7) presence of imperfect interface surfaces; 8) presence of internal (mostly at the interface) physico-chemical phenomena, etc.
The most common way to treat such problems has been to seek a solution by doing numerical experiments over more or less the exact morphology of interest. This leads to heavy use of large computers to solve large algebraic statements. The treatment and analysis of the results of such a Direct Numerical Modeling (DNM) is difficult and needs to follow some guidance "known" for averaging, whether ensemble or volumetric.
What is vital, that these Detailed Micro-Modeling - Direct Numerical Modeling (DMM-DNM) numerical approaches, methods are using as a common value tool the Homogeneous Gauss-Ostrogradsky Theorems when summarizing in COHP (Conventional One-scale Homogeneous Physics) the Lower scale calculations or even for analytical solution fields for the Upper scale, and that is erroneous.
We have shown in many sciences, places in this website, by means of the Two scale solutions, especially with the exact Two scale solutions of those few common textbooks known problems, see in -
that this new kind of Mathematical Physics old problems - the two-scale problems can be successfully tackled and solved exactly on both scales.
While also obtained after 2002 the analytical solutions of the following classical problems that have not been solved for many decades by other methods (given in textbooks the Lower Homogeneous scale "solutions" are wrongly attributed to the Upper Heterogeneous scale averaged fields)
These solutions leave no chances for calculations or comparison with experiment of the Upper scale characteristics using the basis of Homogeneous GO of COHP. This has no sense, invalid for Heterogeneous problems.
In various parts of this website we also have been analyzing the used now, proclaimed as the multiscaled, physically sounded etc. methods, approaches dealing with Heterogeneous, scaled media. We need to do this as long as the large population in physics scientific and engineering communities studying these issues have no desire to learn something more mathematically challenging than what they had been taught in their educational years.
And on the other hand, most of mathematicians have no qualification, knowledge and understanding of genuine physical problems, but considering mathematical tasks in established fields with mathematical statements known for decades.
Meanwhile, the HSP-VAT (Heterogeneous Scaled Physics-Volume Averaging Theory) presents an incredibly powerful tool for dealing with complex heterogeneous media problems - those are just the prevailing number in physics and technologies that having features like those enumerated above. The equations resulting from the use of HSP-VAT methods have strange additional integro-differential terms that are not usually seen in the Lower scale equations [1-10,14-27].
One needs to ask whether or not these new terms are small enough to ignore. In the above mentioned studies and exact solutions, as well as throughout the whole this website information we have shown that they are not. In fact, they are of the same order of magnitude as the terms that are normally kept - see for the two-scale exact solutions in the 7 links-references above with the publications, also in many other ours (published and unpublished) solved problems as well as of researchers involved in the HSP-VAT investigations.
An important aspect of heterogeneous medium transport theory is the development of appropriate boundary condition equations for both (at least) scales in addition to the equations governing transport in the internal region. Most existing treatments conveniently rely upon the first (I), second (II) or third (III) kind boundary conditions for heat, potential, mass, momentum or other field transport. However, the I, II and III kind boundary statements are insufficient for Heterogeneous portions of the near-boundary regions and as a basis for the upper scale boundary conditions direct formulation. There are numerous ways to account for the additional including jump terms between phases - heterogeneous (including porous) medium - homogeneous fluid, two heterogeneous (porous) media interface, other heterogeneous media interactions, which need to be addressed.
Few of the well understood scaled HSP-VAT disciplines with some advancement are discussed in the following our publications
and in
These publications embrace only the part of known today HSP-VAT knowledge base for different disciplines. The main features described in these publications are - nonlinearities in governing equations, advancements in experimental applications of HSP-VAT, electrodynamics and engineering applications of two-scale description of scaled processes, many aspects of atomic scales physics outlined using employment of the HSP-VAT: Travkin, [1-3,16-27]; Travkin and Bolotina, [6]; Travkin and Catton, [4,5], etc.
References:
1. Travkin, V.S., "What Classical Mechanics of XVIII Provided in XX Has Done Wrong to the Base of Mechanical Science Including the Classical Mechanics of Continuum Particles and Conventional Orthodox Homogeneous Particle Physics", http://travkin-hspt.com/rottors/classmechwrong/classmechwrong.htm, (2014)
2. Travkin, V.S., Electrodynamics 2 - Elements 3P (Polyphase-Polyscale-Polyphysics), http://travkin-hspt.com/eldyn2/index.htm, (2013)
3. Travkin, V.S.,"Torsion" or Spinning (Rotation) Physics Scaled (SPS), http://travkin-hspt.com/rottors/index.htm, (2013-2014)
4. Travkin, V. S. and Catton, I., "Porous Media Transport Descriptions - Non-Local, Linear and Non-linear Against Effective Thermal/Fluid Properties," Advances in Colloid and Interface Science, Vol. 76-77, pp. 389-443, (1998).
5. Travkin, V.S. and Catton, I., Transport phenomena in heterogeneous media based on volume averaging theory// Advances in Heat Transfer, New York, Academic Press, Vol. 34., pp.1-144, (2001).
6. Travkin, V.S. and Bolotina, N.N., "The Classical and Sub-Atomic Physics are the Same Physics," http://travkin-hspt.com/parphys/pdf/51_PrAtEd-QM-Ref-2HSPT.pdf, (2013)
7. Whitaker, S., "Diffusion and Dispersion in Porous Media," AIChE Journal, Vol.13, No. 3, pp. 420-427, (1967).
8. Whitaker, S., "Simultaneous Heat, Mass and Momentum Transfer in Porous Media: a Theory of Drying," Advances in Heat Transfer, Vol. 13, pp. 119-203, (1977).
9. Whitaker, S., "Flow in Porous Media I: A Theoretical Derivation of Darcy's Law," Transport in Porous Media, Vol. 1, No. 1, pp. 3-25, (1986a).
10. Whitaker, S., "Flow in Porous Media II: The Governing Equations for Immiscible, Two-Phase Flow," Transport in Porous Media, Vol. 1, No. 2, pp. 105-125, (1986b).
11. Koch, D. L. and Brady J. F., "Dispersion in Fixed Beds," Journal of Fluid Mechanics, Vol. 154, pp. 399-427, (1985).
12. Kheifets, L. I. and Neimark, A. V., Multiphase Processes in Porous Media, Nadra, Moscow, 288 pages, (in Russian), (1982).
13. Cushman, J.H., "Hierarchial Problems: Some Conceptual Difficulties in the Development of Transport Equations," Presented at the International Seminar of the International Centre for Heat and Mass Transfer, Dubrovnik, Yugoslavia, May 20-24, 13 pgs., (1991).
14. Gray, W.G. and Hassanizadeh, S.M., "Averaging Theorems and Averaging Equations for Transport of Interface Properties in Multiphase Systems," Int. J. Muliphase Flow, Vol. 15, No. 1, pp. 81-95, (1989).
15. Gray, W.G., Leijnse, A., Kolar, R.L., Blain,C.A., Mathematical Tools for Changing Spatial Scales in the Analysis of Physical Systems, CRC Press, Boca Raton, (1993).
16. Travkin, V.S., "Reductionism and/versus Holism in Physics and Biology - are Both Defective Concepts without Scaleportation," http://travkin-hspt.com/fundament/scaleport/scaleport.htm, (2004)
17. Travkin, V.S.,"The Major Forces Have Been Missing From Governing Equations for Dynamics of Sub-atomic and Continuum Particles, Bodies in XVIII - XX ", http://travkin-hspt.com/rottors/forcemissing/forcemissing.htm, (2014)
18. Travkin, V.S., What's Wrong with the Pseudo-Averaging Used in Textbooks on Atomic Physics and Electrodynamics for Maxwell-Heaviside-Lorentz Electromagnetism Equations, http://travkin-hspt.com/eldyn/maxdown/maxdown.htm, (2009)
19. Travkin, V.S., Incompatibility of Maxwell-Lorentz Electrodynamics Equations at Atomic and Continuum Scales, http://travkin-hspt.com/eldyn/incompat/incompat.htm, (2009)
20. Travkin, V.S., Particle Physics - Heterogeneous Polyscale Collectively Interactive, http://travkin-hspt.com/parphys/index.htm, (2011)
21. Travkin, V.S., Particle Physics (Particle Physics 2). Fundamentals, http://travkin-hspt.com/parphys2/index.htm, (2013)
22. Travkin, V.S., Nuclear Physics Structured. Introduction, http://travkin-hspt.com/nuc/index.htm, (2006-2013)
23. Travkin, V.S., Statistical Mechanics Homogeneous for Point Particles. What Objects it Articulates? http://travkin-hspt.com/statmech/index.htm, (2014)
24. Travkin, V.S., Solid State Polyscale Physics. Fundamentals, http://travkin-hspt.com/solphys/index.htm, (2014)
25. Travkin, V.S., Continuum Mechanics of Heterogeneous (Ht) Media; Elasticity, Plasticity, http://travkin-hspt.com/elastic/index.htm, (2005)
26. Travkin, V.S., Experimental Science in Heterogeneous Media, http://travkin-hspt.com/exscience/index.htm, (2005)
27. Travkin, V.S., Atomic and Subatomic Physics 2 - Elements 3P, http://travkin-hspt.com/atom2/index.htm, (2003-2015)
In the Bibliography Section below are given more references to publications on Fundamentals of the HSP-VAT. Meanwhile, we need here to take note of that the Bibliographies and References in this website are not maintained up to the latest fresh publications. There is no necessity in this so far. The noticeable publications on VAT and HSP-VAT are rare events. For that reason we do comments, analysis of some works, often just related to HSP-VAT topics and intentions, selectively.