Are there any other Methods and Theories available?

There were numerous methods and theories developed for heterogeneous media applications during more than hundred last years. That needs to be said also that the new wave of "multiscale" theories appeared since ~1990s years due to new fashion toward Multiscaling of physical phenomena.

Practically all of them are the One scale (Upper) approximate (often ad-hoc) theories - when after brief acknowledgment that there is the low scale physics and its mathematical models do exist, the further description focuses completely at the Homogeneous physics (used homogeneous GO theorem) of the Upper scale with the same kind (it is supposed to be no difference at all with mathematics or used almost the same homogeneous equations with the small variations of the source terms, source terms is the Magic Bullet in these "theories") of mathematics and homogeneous governing equations (GE's). Then, the variety of "coupling," "bridging" methods is suggested.

Some claims were developed during the last 10-15 years, when workers started to connect the Lower scale Homogeneous each-phase models, solutions to the kind of "Upper" scale assessments, coefficients while saying no word or model regarding that "Upper" scale nonlocal field, phenomena, or/and governing equations. Meaning, that reader does that himself or knows that?

In materials science, physical chemistry there are numerous methods appeared that connect the two neighboring scale physical models - most popular are the molecular (atomic) and continuum mechanics scales, with application of ad-hoc adjusting techniques that give some appropriate results at the moment, group of problems, etc.

Well, in this way authors play infinite kind of models and pseudo-theories. No Scaleportation strict or valid means are concerned via these ad-hoc "multiscalings." The important thing is how to better find out the Bulk Coefficients for that homogeneous Upper scale mathematical models and GE's?

We address most of noticed modes of pseudo-averaging, "multiscaling," etc. in our web sections and sub-sections.

Through the years we collected actually many reviews and analytical texts with regard of various methods and theories people developed and used for mathematics of transport in heterogeneous media. Few of the most relevant and obvious remarks are given here.

The starting point for multifluid, multiphase medium theories examination was just the analysis of the studies done at that time by the very active and well known researcher Dr. Yu.Buyevich - Buyevich's works ()

Then, as long as the research field of Dr. A.Prosperetti is in the same multiphase media transport arena we started to analyze his publications and few remarks from the more prolonged texts are in -

Few Remarks on Prosperetti's studies ( part 1,)

Few Remarks on Prosperetti's studies ( part 2,)

Some concluding observations must follow the above texts as we want to summarize the only few published approaches in stochastic ensemble averaging and the volumetric method (VAT) of averaging in multiphase transport - ()

One of the latest examinations of understanding of heterogeneous media field formulations in the turbulent transport in porous structures published in - Discussion: "Alternative Models of Turbulence in a Porous Medium, and Related Matters" ()

which reflects on the publication by Prof. D.Nield - "Alternative Models of Turbulence in a Porous Medium, and Related Matters" ()

In few other subsections-physical sciences we are making remarks (with some delays due to alleged expectations for positive outcomes) regarding an Averaging, Multiscaling etc. procedures that might be developed in published works.

07-dd-2004 (written and published on) - Unfortunately, the state of affairs with education on the Two and more scale multiphase (and multiphysics) problems in many fields (sciences) are close to what happened in Meteorology through the last 25-30 years when the wrong governing equations and mathematics of the Upper scale equations has being taught to students through all these years. See our analysis and summaries on that in -

"Modeling and Averaging in Meteorology of Heterogeneous Domains - Follow-up the NATO PST.ASI.980064"

and in

"Experiments, Experimental Data Reduction and Analysis; Numerical Experiment (Simulation) Data Mining."

The similar situation with the Multiscaling, Multiphase, Hierarchical concepts and treatment of those problems in Continuum Mechanics through the last ~30-35 years, see our investigation in -

"What is in use in Continuum Mechanics of Heterogeneous Media as of Through ~1950 - 2005 ? "

10-dd-2012 (completed and published in this month) - Recently we have finished a few analytical texts regarding the current state of affairs in Hierarchical Scaled Physics, primarily addressing the fields of Fluid Mechanics, again spotting the work of A.Prosperetti as an important figure in the field of polyphase transport, see in:

"Homogeneous Mathematical Schemes for Heterogeneous Multiphase Fluids - 14 Years After 1998 Analysis and Criticism"

and in Heterogeneous Particle Physics

"What's Going on in Particle Physics with Homogeneous Approach?"

~1999 - 2001; (what is down here was written and published in) -

We encourage submitting manuscripts and reports for being analyzed under the angle of heterogeneous HSP-VAT - Inquiry form for visitors

In the following table the heterogeneous media treatment features including the few most known approaches, methods, and theories are compared with the HSP-VAT properties -

COMPARISON OF METHODS AND SOFTWARE FOR HETEROGENEOUS MEDIA MODELING AND SIMULATION

	METHOD and SOFTWARE
FEATURE	Software by Using the Scaled Two-Phase HSP-VAT (HiPhyTech)	Two-Phase Traditional Existing Engineering and Scientific Theories and Software Based on HGOT… (the best is via the DMM-DNM)	Homogenization Theory and Software	Monte-Carlo Methods
Domain Problem Formulation as a 2-Scale Problem - #1	X		X*
Boundary Conditions (BC) for the Lower (1st) Scale	X	X	X	X
Two-Scale BC for Heterogeneous Media - #2	X
Effective 1st Scale (lower) Coefficients	X	X	X	X
Upper(2nd) Scale Effective Coefficients - #3	X	X*
Bulk (Volumetric) Properties for HtMM - #4	X	X**	X**	X**
Top-Down Problems Formulation for the Both Scales Field Equations - #5	X
Top-Down BC Formulation for the Both Scales	X
Effects of Interface and Grain Boundaries - via direct Input Into Governing Equations (GE) - #6	X
Effects of Morphology of Each Phase - via Direct Input Into GE - #7	X
Interaction of Each Phase Physical Fields Between Themselves - via direct Input Into GE - #8	X
Heterogeneous Media Experiments - Upper Scale Data Reduction - #9	X
Discrete - Continuum Gap Closure or Simulation for the DMM-DNM and the HSP-VAT - #10	X
Spatial Inhomogeneity of Heterogeneous Media Properties Handling - #11	X

* - Traditional agreement in favor of this statement is not valid (incorrect)
** - Except the dynamic involved variables or parameters with the differential operators used for the definition

HGOT - Homogeneous Gauss-Ostrogradsky Theorem
DMM-DNM - Detailed Micro-Modeling - Direct Numerical Modeling

#1 - The Two-Scale problem formulation means that there are two (2) spatial scales in the physical problem, such as the most recognized problems with - porous media, composites, two- or more phase heterogeneous medium, material or process. This fundamental issue is often not recognized and not given a proper handling, because the general perception is that it is the untreatable problem for having the strict level of scientific approach. Even if the bulk physics of the problem is the same on both scales, the governing equations for the heterogeneous media are dramatically different for each scale.

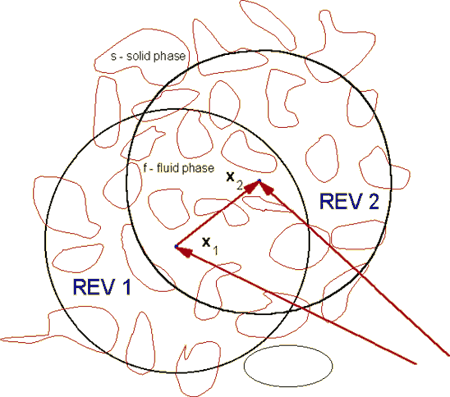
Representative Elementary averaging Volumes (REVs) with the fixed points of representation

#2 - The boundary conditions for each scale of the two-scale media need to be different even for the same physical problem stated as, for example, for the porous medium fluid mechanics.

#3 - Effective coefficients for transport phenomena on the second (upper) scale in the two-scale heterogeneous medium problem need to be evaluated as the scale dependent (depending on the neighboring scales physical phenomena) properties. As such, these coefficients are to be calculated in accordance with a more complex procedures, formulae then used to be in a conventional assessment methods (see Travkin and Catton, 1998, 2001a,b,c; Travkin, 2001; Travkin et al., 1999)- see this website sub-sections on "Effective coefficients".

#4 - The bulk static properties (named as such for the absence of participation of derivative operators in the mathematical formulation) are calculated as mean volumetric values, even for the methods called as "stochastic". There are quite different mathematical formulations for dynamic (with the inclusion of dynamical, derivative-dependent components) bulk variables in Heterogeneous and hierarchical Media Modeling (HtMM).

#5 - Quite often the primarily forceful impact (influence) on the volume or piece of medium starts with an application of an external field onto the heterogeneous medium as it is applied on over the upper scale material-field interaction. In this situation the secondary, following physical phenomena are formulated on the lower spatial scale after formulation the problem on the upper (still initial) scale. And this is just the reverse order of conventionally understood physical and mathematical model sequence, other than the usual Bottom-up sequence of models.

#6 - There is no other mathematical theory (or science, including the homogenization theory with its variety of mathematical formulations) than the HSP-VAT that provides the direct description of the interface (grain boundaries, etc.) surficial physical phenomena through the mathematical formulation in the problem's governing equations as via the parts (terms) of those equations or boundary conditions of the problem.

#7 - The morphological features (geometry, topology) of each phase are present (exist) in the formulation of the two-scale HSP-VAT problem in the governing equations directly.

#8 - There is also the explicit, direct presence of the phase-to-phase interaction of physical fields in the HSP-VAT GE.

#9 - So far, as we have been observing up to the nowadays situation (), there is no one explicit, direct involvement of any heterogeneous media modeling theories into the mainstream of experimental science, but the HSP-VAT. What is known as implementation of any heterogeneous theory, but HSP-VAT, is the pure incorrect mathematics and physics under the umbrella of "heterogeneous" words. Meanwhile, it is the simple and obvious statement that the physical and mathematical models for physical phenomena, or processes should be of the same nature for the theory needs as well as it should serve for an experiment. The homogeneous matter is well suited with the HGOT, which is unfortunately not the case with the heterogeneous media served so far mainly with the mathematical models developed for HOMOGENEOUS media.

#10 - The mode, the ability to perform mathematical modeling via computer simulation gave birth to many great discoveries. As for today's mode to apply this way of studying toward the heterogeneous medium phenomena, the question arises about what is the relation between the Detailed Micro-Modeling - Direct Numerical Modeling (DMM-DNM) and the upper scale physical phenomena? As it seems that the very purpose and existing goal of modeling via the DMM-DNM is to find out the relation not for a pure DN modeling of phenomena on the lower scale medium, but to access the properties of the medium and of the process in that medium which is being characteristic for the medium as for a whole on the upper scale of consideration. Only the VAT treats correctly this scale transition because the HSP-VAT uses the correct heterogeneous Volumetric-Surficial structure-properties connection theorems, as the Whitaker-Slattery-Anderson-Marle (WSAM) theorem, which is being the first one directly applicable to the nature of the problem.

#11 - When the heterogeneous medium changes its properties throughout the space, mainly inside the problem's domain, there is the issue of how to incorporate these changes within the upper scale problem understanding and consequently into the GE of the problem. The lower scale coefficient's spatial changes are not the only valid features, which need to be incorporated into the upper scale GE. The HSP-VAT provides this input naturally via application of the various heterogeneous WSAM kind of theorems.

Collaborators in Continuum Mechanics HS Sciences: