As in other sciences - sections of this website when reviewing the current or last years publications as the evidence of how the organized government financed science is doing in this or that science or large enough field in science - our goal is not to find out some real breakthrough, unfortunately it is the very rare event, but to find out what is considered in Conventional Orthodox Homogenous Physics (COHP) or Homogenous (Hm) Biology, Biophysics as the "state of the art" and give to this "state" some analysis and critique that inside of the box workers won't write about because of fear for their positions.
But to only a handfull publications, that are or of immediate interest to us or the works are just happened to be on the table at a proper time for the review.
Again, nothing of personal interests unless the research is of outstanding worker as, for example, Craig Venter, Luc Montagnier, some other personalities, or of new pioneers in the fields.
Blood Flow and Cancerous Tumor Growth=============================================================================================
Paper:
"We investigate a three-dimensional multiscale model of vascular tumour growth, which couples blood flow, angiogenesis,
vascular remodelling, nutrient/growth factor transport, movement of, and interactions between, normal and tumour cells,
and nutrient-dependent cell cycle dynamics within each cell. In particular, we determine how the domain size, aspect ratio
and initial vascular network influence the tumour's growth dynamics and its long-time composition. We establish whether it
is possible to extrapolate simulation results obtained for small domains to larger ones, by constructing a large simulation
domain from a number of identical subdomains, each subsystem initially comprising two parallel parent vessels, with
associated cells and diffusible substances. We find that the subsystem is not representative of the full domain and conclude
that, for this initial vessel geometry, interactions between adjacent subsystems contribute to the overall growth dynamics.
We then show that extrapolation of results from a small subdomain to a larger domain can only be made if the subdomain
is sufficiently large and is initialised with a sufficiently complex vascular network. Motivated by these results, we perform
simulations to investigate the tumour's response to therapy and show that the probability of tumour elimination in a larger
domain can be extrapolated from simulation results on a smaller domain. Finally, we demonstrate how our model may be
combined with experimental data, to predict the spatio-temporal evolution of a vascular tumour."
We are making here a criticism for educational purposes, as we made this kind of critique many times in various fields and sciences. There is almost no professional interest in this time waste, but only for students demonstration what is the difference with the Conventional Orthodox Homogeneous Physics (COHP) or (Hm) Biology, Biophysics understanding and the HSP-VAT Physics 2, Ht Biology 2, Ht Biophysics 2 philosophy and methods. Sometimes the excerpts are of a few sentences - that is because for better grasping the way of thoughts.
Orthodox - because the main points of this approach (HSP-VAT) to the Hierarchical Scaled phenomena in Physics 2 are known for >45 years already. That means competent professionals know about HSP-VAT for many years, still don't follow in this direction because it requires the re-educating himself effort, high probability of job loss and dishonest attitude from colleagues.
And people after their 30-40 don't like to educate themselves too much or at all.
In p. 1 we can find that:
"..... Angiogenesis is initiated when hypoxic cells secrete
tumour angiogenic factors (TAFs), such as vascular endothelial
growth factor (VEGF) [3,4]. The TAFs are transported through
the tissue by diffusion where they stimulate the existing vasculature
to form new sprouts. The sprouts migrate through the tissue,
responding to spatial gradients in the TAFs by chemotaxis. ......"
Our comments:
The word "factor" is usually explored when there is no more professional, field's terminology pertained to the explanation of phenomenon(a).
So, here the words TAF and VEGF are because biologists cannot formulate them more professionally, at least in terms of bio-chemistry and biophysics as they can and like to do typically.
In the same p. 1 we can find more interesting notes regarding the understanding of contemporary medicinal, biological methods by authors among them are a lot of mathematicians specializing in biology:
" Tumour growth and angiogenesis can be modelled using a
variety of approaches (for reviews see [9,10]). Spatially-averaged
models can be formulated as systems of ordinary differential
equations (see [11,12]). Alternatively, a multiphase approach can
be used to develop a spatially-structured continuum model that
describes interactions between tumour growth and angiogenesis
and is formulated as a mixed system of partial differential
equations (PDEs) [13].
Alternatively a 2D stochastic model that
tracks the movement of individual endothelial cells to regions of
high VEGF concentration is introduced in [14]. Following [14],
McDougall and coworkers [15] have developed a model for
angiogenesis and vascular adaptation in which the tissue
composition is static and attention focusses on changes in the
vasculature. This framework was then extended by Stephanou
et al. [16] to produce the first 3D simulations of angiogenesis and
vascular adaptation. "
Our comments:
There is a fashion to call everything taken at different scales as a "multiscale." This is not correct usually, because the connection of these "scales" is merely semantic.
People combine the consideration related to different spatial and temporal scales and saying -- it is a "multiscale" modeling. It's a professional joke, but not a multiscale approach.
It is usually in most of biology, biophysics and medicinal studies an arbitrary, physically and mathematically groundless, lump sum of each scale related models (partial) and adjustments.
Some authors (main) of this paper have been started to use the terms and language of "multiscale" biological and mathematical models only in ~2005 (before that year they did not know this word probably), while this science has been existed since ~1967-70!
Their "multiscale" like models is not multiscale ones strictly speaking.
In spite that many authors of this reviewed paper are mathematicians, they don't look around much about "multiscaling".
In the p. 2 we can find:
"More recently, Macklin et al. [17] coupled a
multiphase model to a discrete model of angiogenesis that
accounts for blood flow, non-Newtonian effects and vascular
remodelling. The models are coupled in two ways: via hydrostatic
pressure which is generated by the growing tumour and acts on the
vessels, and via oxygen which is supplied by the vessels and
stimulates growth.
Our comments:
We have made a review of this paper (see below), while here might mention that their model is not "multiscale," is incorrect in momentum transport physics as well as regarding the "non-Newtonian" feature, etc. etc.
More in the p. 2 we can find:
"... In separate work, Owen et al. [19],
building on the work of Alarcon and co-workers [20--23],
proposed a 2D multiscale model for vascular tumour growth
which combines blood flow, angiogenesis, vascular remodelling
and tissue scale dynamics of multiple cell populations as well as the
subcellular dynamics (including the cell cycle) of individual cells.
.... In this paper, we extend the multiscale model proposed by Owen et al. [19] from 2D to 3D...."
Our comments:
We would comment on the present paper with the glance back to the start of this modeling effort -- that not surprisingly takes so far near 10 years of large group financed for studies..
More in the p. 2 we can find:
"Methods
.......Our model is formulated on a regular grid that subdivides the
simulation domain into lattice sites. Each lattice site can be
occupied by several biological cells whose movement on the lattice
is governed by reinforced random walks, and whose proliferation
is controlled by a subcellular cell cycle model. The vascular
network consists of vessel segments connecting adjacent nodes on
the lattice, with defined inflow and outflow nodes with prescribed
pressures. We also specify the amount of haematocrit entering the
system through the inlets.
The vessel network evolves via (i)
sprouting of tip cells with a probability that increases with the local
VEGF concentration, (ii) tip cell movement is described by a
reinforced random walk, and (iii) new connections forming via
anastomosis. In addition, vessel segments with low wall shear stress
may be pruned away. "
Our comments:
All the equations in mathematical model in this work, TextS1 -- (1 -- 5), (6,7), (14 -- 16) belong to the one scale Homogeneous physics mathematical models with only the semantic connection to the physics of the problem.
Equation (16) is for only the straight pore (pipe, blood vessel) laminar Stokes flow.
The model's mathematical formulation was definitely intended to be as of polyscale nature, while it is not neither polyscale nor even the correct in physics and math the one-scale equations.
More in the p. 2 we can find that:
" Elliptic reaction-diffusion equations for the
distributions of oxygen and VEGF are implemented on the same
spatial lattice using finite difference approximations, and include
source and sink terms based on the location of vessels (which act as
sources of oxygen and sinks of VEGF) and the different cell types
(e.g. cells act as sinks for oxygen and hypoxic cells as sources of
VEGF). The flowchart in Figure 2 summarises the algorithm and
shows how processes that act on different space and time scales are
accommodated. In summary, after initialising the system, the
diffusible fields, cellular and subcellular states are updated
(including cell division and movement), before the vessel network
is updated, this process being repeated until the simulation ends.
Further details about each step of the computation and the model
parameter values can be found in the Text S1. The model is
implemented in C++, using CVODE (https://computation.llnl.
gov/casc/sundials/main.html) to integrate the subcellular ODEs,
and SuperLU (http://crd.lbl.gov/,xiaoye/SuperLU/) to solve
the linear systems for the flow calculation."
Our comments:
So, this is a one-scale Homogeneous model of the p.d.e. with the sources, as it should be in a one-scale mathematical model.
In p.3 we can find that:
"... Periodic
boundary conditions are implemented for the random walks of the
cells (including endothelial tip cells), for the vessel network and
flow calculation, and for the reaction-diffusion equations. In order
to integrate more closely with experiments, an interface is
implemented to import experimentally-derived vascular network
data, in order to specify the initial vasculature and then apply the
tumour growth and angiogenesis model. The 3D results are
visualised in Povray (http://www.povray.org) and OpenInventor
(http://oss.sgi.com/projects/inventor/)."
Our comments:
Periodic Boundary Conditions (BC) are not correct for this kind of problems.
In p. 3 we can find more:
"Results
3D vascular tumour growth
The results from a typical simulation showing the development of a tumour and its associated network of blood vessels are
depicted in Figure 3. Simulations were performed on a 50\50\50 lattice with spacing Dx~40mm, which corresponds
to a 2mm\2mm\2mm cube of tissue. For the following simulations, each lattice site can be occupied by at most one cell
(either normal or cancerous), which implies that, for the grid size used (40mm), the tissue is loosely packed. A small tumour was
implanted at t~0 in a population of normal cells perfused by two parallel parent vessels with countercurrent flow (i.e. the pressure
drops and hence flows are in opposite directions). Initially, insufficient nutrient supply in unvascularised areas causes widespread death of the normal cells. .... "
Our comments:
The one cell in 40mkm -- means that there is no physical cell presence is modeled. The model plays with the mathematical objects. There are no physical cells, no cells objects, no tissue at all.
There are imaginary assigned subjects of healthy medium, cancerous tumor, and endothelial cells and assigned initial blood vessels network.
These objects supplied by mathematical rules for their interplay.
There is no sense to consider, comment on the further results - BUT Figures!
"Figure 1. Multiscale model overview (interaction diagram). This figure shows the connections between the different modelling layers. In the subcellular layer the cell cycle protein concentrations and the p53 and VEGF concentrations are modelled via systems of coupled ordinary differential equations. The local external oxygen concentration influences the duration of the cell cycles. Cells consume oxygen, and produce VEGF in the case of hypoxia. Extracellular VEGF also influences the emergence of endothelial sprouts and their biased random walk towards hypoxic regions. If endothelial sprouts connect to other sprouts or the existing vascular network, new vessels form. Vessel diameter is influenced by the local oxygen concentration and flow-related parameters, such as pressure and wall shear stress. The vascular network delivers oxygen throughout the tissue."
Our comments: Given in Fig. 1 here is the schematic of subcellular, cellular and tissue models that are connected by medical semantics and with the mathematical assigned algorithms.
There is no physics (real biochemistry) involved.
The scheme is completely mathematical -- the mix of discrete algorithms plus the differential One Scale (sub-cellular scale) equations for chemical substances transport.
It is completely imaginary construction (IC), with no scale physics, no proper hierarchical mathematics.
"Figure 2. Multiscale model overview (flowchart). The flowchart shows the temporal sequence of the computational steps in our simulation."
Our comments:
As we wrote above on the TAFs (factors) and VEGF (factor) are the summarized factors -- physical variable-fields from the Below-scale pertinent phenomena models, comparing to the scales actually taken into account in this study.
As in ever appearing in medicinal literature -- the scales and scale physics (biophysics if someone likes) are communicated just on the semantic, algorithms designed base. There is no correct physical, mathematical and chemical interscale connection applied as seen in the Figs. 1,2.
"Figure 5. Schemes of numerical studies. A) We consider two parallel vessels running in the x-direction and centred with respect to the variable z-extension, with equal mean pressures and opposite pressure drops. B) We analyse how the interference between neighbouring subsystems influences the behaviour in a larger domain: Bi) We consider a large (50\50\50) domain, where all 10 subdomains, each with two parent vessels, are allowed to interfere with each other and farfield communication is incorporated in this setting. Bii) Depicts a 50\50\10 subsystem with two parent vessel pairs. Thus nearfield (but not farfield) interaction in the z-direction is now included. Biii) The most restricted example, a single 50\50\5 subdomain, thus preventing all communication in the z-direction. In A) and B) we apply reflecting (zero-flux) boundary conditions.
C) Different boundary conditions are considered: Ci) Periodic boundary conditions in the y- and z-direction. The grey subdomain is effectively surrounded by other networks. Cii) Periodic boundary conditions in the z-direction only, which should produce similar behaviour to Bi)."
Our comments:
These Figures 5 and 9, and (1,2) are the pure essence of the incorrect heterogeneous media modeling and simulation.
We can talk on many wrongly accounted physics and math features ( and we will make it below), but mentioning here just the four ones, that might be the globally main features for failure.
Those features are:
1) Incorrect definition and conceptual design of REVs domains in Fis. 5,9. What authors name the "domain" is the REV -- should be, which is a Representative Elementary Volume (REV), coined as such more than 30 years ago, when these authors probably went to school, some of them.
And the REV assignment is incorrect -- we wrote intensively on this subject in many spots of this website and in hard copy publications.
For example, the REV's bounding surfaces DO NOT INTERSECT the both phases as they should be.
Authors don't know -- Why is that? Actually they DO KNOW Why? They don't know just related thing - How to avoid that Why, because they don't know the basics of Hierarchical Heterogeneous mathematics and physics. Who can help?
2) The absence of a tissue, actually with the funny explanation of the tissue presence in the model. The model really is the one-phase formulated.
3) Incorrect "averaging" -- means of a scale representing models. There is no averaging at all. We are surprised by this fact as a few mathematicians in the team did not go through the literature to learn -- what is the averaging all about?
4) Incorrect Boundary Conditions (BC). No sense to talk about "correctness" or "influence" of such BC.
Among other really numerous defects of this modeling effort in the paper by Perfahl at el. [2011] can be mentioned also:
5) One needs to read our critique of Continuum Mechanics studies (mathematically and ideologically they are close to the present study, and a serious studies of the present pool of authors) of Kushch at el. in --
6) There are no correct phase related governing equations in this study.
7) There is no correct interphase exchange in this study.
8) There is no correct blood flow model in this study. Blood is the polyphase medium.
9) There are no vessels and tissue soft solid media models here as well. Without these models -- there are no correct blood transport in this model. We are not talking about the tumor growth model, because it is much more complicated thing.
The present authors are not ready for comprehension of what is about to comprise within this field, nevertheless they started to getting funds for this?
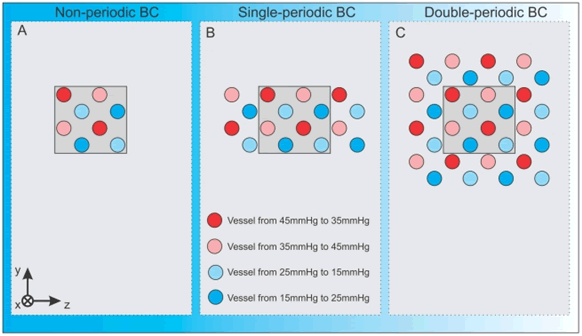
"Figure 9. Multi-vessel basic vascular unit. A) A basic parent vessel unit that includes eight vessels with equal pressure differences, but with four different mean pressures, arranged so that the nearest parent vessel in each case is at a different mean pressure, which should enable functional vessels to form within and between subdomains. Non-periodic means that we consider reflection boundary conditions in all directions. B) Periodic boundary conditions in the z-direction. C) Periodic boundary conditions in the y- and z-directions."
Our comments:
This is the error that will be placed in the encyclopedias of biology, physics and mathematics - How the Homogeneous description of biomedia and problem in them are different from a Heterogeneous Scaled (at least two scales) polyphase models (correct ones).
The "solutions," simulations of the problem stated are not worth to consider as such while the initial concepts and mathematical statements are incorrect.
Note -- that there is the one only phase being intersected by the boundary surfaces of the REV!
On purpose? What is the purpose of keeping one only phase divided by bounding surfaces?
Authors should learn from Dr. V.Kushch to do that --
He does this craft of one phase REV in much more sophisticated ways.
Our comments:
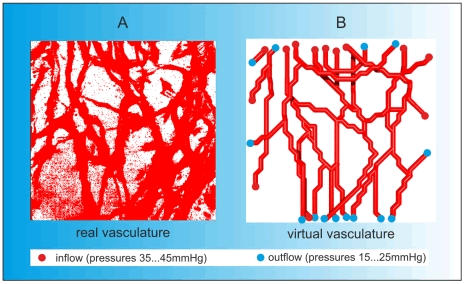
"Figure 13. Image reconstruction. We reconstructed the vascular network by applying the following strategy. 3D multiphoton fluorescence microscopy images (A) taken from mouse models in vivo formed the basis of our geometrical reconstruction. These images were transferred to OpenInventor and Matlab for image analysis. Based on the data we reconstructed the vascular graph model that describes the connectivity of the vascular network. B) We assigned inflow (red points) and outflow nodes (blue points) at various pressures in order to obtain a persistent and stable network. The vascular graph is characterised by the spatial coordinates of the nodes and the connections between them."
Our comments:
Note and this is important that the diameters of generated vessels are of the one scale pores with the OpenInventor and Matlab software that is known have no features of scaled fluid mechanics. Still, the great difficulty is that the vascular network is the polyfluid-soft-polysolid Heterogeneous transport system with only partially assigned exchange of substances. Model for this one of the main component of tumor growth should be really polyscale Hierarchical.
Summary:
1) There is no tissue dynamics (locomotion of tissue as a polyphase medium) in this study; no sub-cellular dynamics as allegedly stated in this paper -- but discrete mathematical algorithms that describe the "imaginable" processes, pretty complicated polyphysics processes.
2) What are these "diffusion' "reaction" p.d.e. for "p53' and VEGF macromolecules?
And what is the tissue in which they are spreading -- "diffuse"?
We can respond to these questions -- the "p53" and TAFs (tumor angiogenic factors) as VEGF (vascular endothelial growth factor) are the biopolymeric huge molecules not of atomic size.
That means they (macromolecules) do not "diffuse" -- but they are transported in a polyphase extracellular matrix (ECM) by a number of forces.
The ECM medium is not just soft homogenous solid, it is a polyphase soft porous solid (elasto/plastic) with the fluids and particulate phases that are migrating in it (solutions, lymphatic debris, soft elastic particles).
It can be said that this kind of modeling for the medical/mathematical communities right now, even in 2011, is a way too premature the move to have a hand on that complexity.
3) As we wrote above and in many spots in the web (this sentiment is out of academic publishing), these communities should be of some kind of knowledge, skills in scaling, in HSP-VAT, in major physical phenomena modeling for polyphase, polyscale media, etc.
Nothing of this right now in their possession, that is why we observe such Homogeneous, allegedly "multiscaled," with the broken physics and mathematics modeling effort.
Never mind, if workers would learn from HSP-VAT tools then in a 5-8 years they might start to get to polyscaling correctly.
4) Also, the another kind of scenario of the slow progress is not unknown in medicine ( and science in general) throughout the XX century. In this mode of scientific "progress" the incremental improvements, advancements are made of the controlled, small steps that allowing researchers to live all the professional life exploring this pleasant smooth path of tiny advances.
In this way the proposals and projects are being downgraded to the level of more common or lower level reviewer, even a single lower level reviewer can kill the project.
5) Also, there are existing temporary attractions to one or another fashion (mode) in using methods, techniques while doing studies. Right now in physics and many technologies for a few last years it is a fashion to call everything as a "multiscale," "multiscaling." Before that it was the "nanotechnologies" magic word. In 99% these works are of old Continuum -- discrete physics, methods.
Conclusions:
1) Now, after ~18 years of our officially recorded commence in the US (2003-2004) of the biological, medicinal, blood transport modeling research (this review is written in 2011), and of the proposal to NIH on that topic for muscles in 2004 --
we can see that the time and money spent by NIH and NIC, European programs for blood transport modeling and cancer tumor genesis research support are poorly spent.
In our proposal of 1994 the outsmarting features (features that current generation of medical-biophysical-mathematical professionals cannot apprehend. That most of authors that now are writing on "multiscale" topics:
They can not overcome "the historical feature of inhibition of apprehension, I ascribe the hypothesis of formation of inhibiting apprehension to what is called "hard wiring" of brain structure by cognitive scientists. People have suspected and taught for at least centuries that once one accepts a theory about rationalized phenomena, that the person can not implicitly understand another kind of theory about phenomena or develop it themselves, and for centuries more, people have believed that it is difficult for someone to change his ideas to accept a new idea;" - by Edward Lewis in his "The Periodic Production of Rationalized Phenomena and the Past Periodic Depressions"
..." )
as, for example :
"polyphase," "two-scale modeling inside of the blood vessels," also as "blood vessels polyphase, polyphysics two-scale wall's modeling," the tissue -- real tissue, not of only by the coefficients exposed involvement in the models, the correct scale based elasticity-viscoelasticity Hierarchical mathematical governing equations and models, and the most thing that may be important -- the knowledge base for that Heterogeneous physics, biophysics, hierarchical mathematics.
One can see also more arguments about apprehension of new phenomena for polyphase physics in our:
The time has gone, and now the only chance for conventionally supported by NIH and NIC research teams is to set up classes, and in a 5-8 years some workers can "apprehend" and begin using the truly multiscale techniques in biology and medicinal research.
Hardly believable thing to imagine, and by the way, we think that conventional science would like to find out the way around as they try to slip through in conventional Homogeneous Continuum Mechanics for >40 years:
Conventional physics slowly apprehends the knowledge of heterogeneous scaled technologies in Heterogeneous Thermophysics, Polyphase Fluid Mechanics, Composites, Chemical Engineering, Meteorology, Particle Physics, etc. etc.
Another examples are the attempts to outdo the shame with the Cold Fusion and Magnet Motors -- the physical things that COHP officially rejected as the nonsense, but "unfortunately" these technologies existing notwithstanding the verdict of COHP.
More of that, the Cold Fusion technology products and Magnet Motors are already in the market!
Many fundamental principal problems standing up front of researchers studying the human vessels fluid transport had been resolved far before the present days (2011) authors obtained their Ph.D.'s in biophysics or medicine (well, some of them).
Among them:
1.1) Presentation of human tissue (soft-solid) and blood, lymphatic fluids (lymph), vessels functioning as a two- or more phase systems (solid-fluid or polyphase in a fluid, and soft-solid polyphase) of the two scales (at least) for modeling --
18-20 years back the NIH proposal:
1.2) Development of the two-scale mathematical statements and the most important - the solutions and study of the basic, fundamental problems in the polyscale Physics 2.
1.3) Development of the methodology, that is extremely important for polyphase flow as of blood, for example, of problem statements for the irregular, curved and stochastic pores (vessels) with polymode fluids transport (laminar, turbulent, intermediate) in a matrix and the mathematical methods for the 2-scale Hierarchical problem of this kind.
1.4) Some portion of this knowledge base (as of 1994) was presented in our proposal to NIH of 1994 and hangs in the internet from ~2003 --
At present level of the HSP-VAT knowledge that proposal is obsolete, nevertheless, the sum of technologies
in it is not achievable by current time researchers in biophysics and medicine.
We wrote about this new for biologists, biophysicists, medicinal professionals knowledge base to many authors in these fields. The usual level of "inhibition of apprehension" had been exhibited.
2) Regarding this paper's review content we can cite from our:
about the similar state of affairs "Other faculties when making study on heterogeneous, famous now "multiscale" topics - they waste the public money, pretending that they can do heterogeneous, multiscale studies. Or they should admit that their qualifications are not good enough to understand the mechanics and physics of HS media.
Unfortunately for .......need to say a word on most of "heterogeneous" like research and publications by MAE and other departments professionals. Few other departments also making themselves the targets for future mockery. Through the years we also tried to make professors at MAE department involved, but without success. These professionals, nevertheless, doing also the heterogeneous and fashioned lately "multiscale" media studies are wasting just their time and public money in a real sense.
They do the incorrect research; some publish incorrectly written books, for decades.
......Anyway, they also doomed to be the Wheel Re-Inventors. There is no other fundamentals exist for doing Heterogeneous Scaled, Hierarchical physics than the HSP-VAT for more than 40 years. Correct fundamentals. They will need to use some elements of HSP-VAT and better sooner than later....."
3) We would like to cite also the words of ~2003 on the Homogeneous "multiscaling" from our:
"Announcements" - http://www.travkin-hspt.com/fundament/Announcements.htm;
"...Of course, technically speaking it might be named the multiscale method when few scales those differentiated one from another just by some coefficient (not by physics) being applied to the same mathematical problem governing equations and to the same physical scale model for each of these scales ? But what is really should be understood under the specific different scale models name in this case - is that it is the MULTIRESOLUTION method.
Meaning, that the same understanding of physical problem and statement is being treated using the different (various) scales for better reflection of the specifics of physics and for easier and better solution of this ONE SCALE HOMOGENEOUS statement problem.
That's it. Nothing more if not HSP-VAT used. Especially, when the task is set about a heterogeneous medium (material).
More than ever, when the problem constituted for a heterogeneous medium or when the scales are different by their peculiar physics - as, for example, the scale of a singular star, planet (or an atom) and the scale of a star nebula (or a piece of solid (or other) state medium). Everybody realizes that the difference is of many orders of magnitude. And the physics on each scale is different. Nevertheless, everything and the physics including are interdependent!
How many physical theories do you know that are capable to describe a variety of interdependent via a scale physics phenomena? ..."
And no, no coefficients thing we are talking about.
4) We had written to authors of this paper on some of their problems with the model and modeling in 2011 and had not published this review at the time. Giving them the time period for an "apprehension" and for turning again to the agencies for a new cycle of funding ?
We will see the result and publish and disseminate the findings regarding the "inhibition of apprehension" of these specific biologist communities of a few countries?
Paper:
"In this article, we present a new multiscale mathematical model for solid tumour growth which
couples an improved model of tumour invasion with a model of tumour-induced angiogenesis. We
perform nonlinear simulations of the multi-scale model that demonstrate the importance of the
coupling between the development and remodeling of the vascular network, the blood flow
through the network and the tumour progression. Consistent with clinical observations, the
hydrostatic stress generated by tumour cell proliferation shuts down large portions of the vascular
network dramatically affecting the flow, the subsequent network remodeling, the delivery of
nutrients to the tumour and the subsequent tumour progression. In addition, extracellular matrix
degradation by tumour cells is seen to have a dramatic affect on both the development of the
vascular network and the growth response of the tumour. In particular, the newly developing
vessels tend to encapsulate, rather than penetrate, the tumour and are thus less effective in
delivering nutrients."
In p. 2 we can find that:
"The aim of this paper is to formulate a
multi-scale mathematical model of solid tumour growth, incorporating three key features:
the avascular growth phase, the recruitment of new blood vessels by the tumour
(angiogenesis) and the vascular growth and host tissue invasion phase."
Our comments:
According to what is written in the paper this is not true as long as authors even don't know -- What is the "multi-scale mathematical model of solid tumour growth" ? What are the equations for a multiscale phenomena?
"Fig. 1.
Schematic of the tumour regions.
and
are the proliferating, quiescent/hypoxic
and necrotic regions, respectively"
Our comments:
This figure depicts the three large Heterogeneous areas with the interphases between all of them. Inside of each region is also the Heterogeneous media and the Multiscale models in each region should consist of Heterogeneous Hierarchical biophysical and mathematical models with only coefficients that might be assigned as for this scale homogeneous fields with the coefficients from the unspecified/specified below spatial/temporal scale, which is of no interest at the moment for this specific biophysical model/process.
In p. 4 we can find that:"In this paper, we couple an improved continuum model of solid tumour invasion (following
[48]) that is capable of spanning the 102 μm-cm scale and accounts for cell--cell, cell--ECM
adhesion, ECM degradation, and tumour cell migration, proliferation, and necrosis with a
model of tumour-induced angiogenesis (following [50]) that accounts for blood flow
through the vascular network, non-Newtonian effects and vascular network remodeling, due
to wall shear stress and mechanical stresses generated by the growing tumour, to produce a
new multi-scale model of vascular solid tumour growth. ....."
Our comments:
What is stated here is the wish-list, but what was performed is the pretty simplified physically and
mathematically model.
"We perform simulations of the multi-scale model that demonstrate the importance, on
tumour invasion of the host tissue, of the nonlinear coupling between the growth and
remodeling of the vascular network, the blood flow through the network and the tumour
progression. ...."
Our comments:
This is not a "multi-scale" model.
In p. 5 we can find at last the start of governing equation's depiction:
"... Since oxygen diffusion occurs more rapidly than cell-mitosis (the time
scale on which the equations are non-dimensionalized), these processes are described by the
quasi-steady reaction diffusion equation
where D is the diffusion coefficient, the parameter
combines the effects of oxygen uptake and decay ....."
Our comments:
This is the Homogeneous one scale diffusion equation with the three conjectural source-terms.
In p. 6 those source terms are described:
"The two remaining terms
and
in Eq. 1 reflect the oxygen-tissue transfer from the pre-existing and
neo-vascular blood vessels respectively, and are given by:
and
where
and
are constant transfer rates from the pre-existing and neo-vascular vessels. "
Our comments:
All these source-parameters are conjectural models. Nevertheless, these processes are from the below physical scales and must be modeled at the lower biophysics scales. With the really another scale(s) models and governing equations. Then it would be the two-three scale exchange models.
In p. 7 one can find :
"2.1.2 Tumour mechanics and the cell velocity---The tumour cells, the ECM and host
(non-cancerous) cells are influenced by a combination of forces which contribute to the
cellular velocity field."
"Following previous work, we assume that all solid phases move with a single cellular
velocity field and we model the cellular motion within the ECM as incompressible fluid
flow in a porous medium. In the future, we plan to use mixture models ...... ."...
Our comments: Very simplified soft solid biomedia modeling concepts.
Further in p. 7 one can find:
".... Accordingly, the non-dimensional velocity is given by
where
is the cell-mobility which models the net effects of cell--cell and
cell--matrix
adhesion,
is the ECM density (e.g. a non-diffusible matrix macromolecule such as
fibronectin, collagen or laminin) and
is the haptotaxis coefficient. ...."
"......... the growth of the tumour is then associated with the rate of volume change:
where
is the non-dimensional net proliferation rate. "
Our comments:
Pretty simplified Homogeneous (mixed) media governing equations, not the multiscale ones.
Further in p. 10 one can find:
".... We model the remaining processes as follows. For the MDE, we take
where
is the nondimensional MDE concentration,
is the diffusion coefficient (assumed to be constant),
and
are
the non-dimensional rates of production of MDE by the viable tumour cells
and the sprout tip ECs, respectively. "
"The ECM density satifies:
where
and
are
the non-dimensional rates of production of ECM by the viable
tumour cells and sprout-tip ECs and
is the non-dimensional rate of matrix degradation by the MDE. "
" Finally, the original ECM and the pre-existing blood vessel density are assumed to be
degraded by the MDE:
Our comments:
All these and some other p.d. governing equations are the Homogeneous media one scale equations with the sorce-terms as was established in Homogeneous physics in XIX - first half of XX.
These are not the Multiscale equations.
Further in p. 12 one can find the model of blood flow in capillary network:
"In order to calculate the flow within the entire interconnected network of capillaries, it is
first necessary to decide upon a local relationship between the pressure
gradient vessel
and flow rate
at the scale of a single capillary element of length
and radius
.
Such a
relationship in the case of a non-Newtonian fluid can be approximated by the following
Poiseuille-like expression:
Our comments:
The most simplistic model for a very complicated and basic process. Even for absolutly rigit pores (vessels) this network flow rate algorithm would be a great simplification.
Finally in p. 12 one can find in Conclusions:
"In this paper, we have coupled an improved continuum model of solid tumour invasion
(following [48]) with a model of tumour-induced angiogenesis (following [50]) to produce a
new multi-scale model of vascular solid tumour growth. ......."
"........Regarding the model, we plan to develop a more detailed analysis of the effect of solid
pressure on the constriction and collapse of vessels in the microvasculature and on the
corresponding response of the microvascular network. We also plan to include the effects of
the venous system. Other features, such as the recruitment of pericytes by the vascular ECs
will also be investigated. In addition, we will incorporate more realistic models for soft
tissue mechanics.
The work presented here demonstrates that nonlinear simulations are a powerful tool for
understanding phenomena fundamental to solid tumour growth. A biophysically justified
computer model could provide an enormous benefit to the clinician, the patient, and society
by efficiently searching parameter space to identify optimal, or nearly optimal,
individualized treatment strategies involving, for example, chemotherapy and adjuvant
treatments such as anti-angiogenic or anti-invasive therapies. This is a direction we plan to
explore in the future."
Our comments:
There is no multiscale physics and mathematics and multiscaling equations here - but the "physiological" like and oncology specific features brought in together just by Algorithms, numerical algorithms.
Computers endure everything workable.
Summary:
1) So - where are the scales, the multiscaling"?
Conclusions:
1) In this paper are so many adjustable coefficients that it is no sense to consider seriously the value of the model as itself, also the results of numerical simulation.
This free set of parameters/coefficients allows getting to a very large manifold of pseudo-solutions.
Any honest consideration of conjectures and equations in sections 2.1.2 and 2.1.3, for example, get to the conclusion that this is the artificial creation of biophysical model of the first part of XX century with the knowledge of some biochemistry of the second half of it.
The only difference is that in the first half of XX there were no really functioning computers -- but the idea and some computers were already known from the XIX, and that there was no computational mathematics for partial differential equations.
2) The tedious search gives an approximate number of adjustable parameters/coefficients as of 47 in this model and study. Most of them are the mathematical conjectures arising from inability to take the problem as it is -- as Hierarchical Heterogeneous Polyscale biophysical problem. Pretty complicated for 7 - 9 people teams.
This is the Manhattan kind of problem if really taken as the Hierarchical Polyscale for a layman to compare.
3) This is the disaster paper. Not in terms of intentional defects, but of gross oversimplifications.
In spite that workers of the paper are all (well not all by the work place), but in reality all are mathematicians, while with the modeling philosophy and mathematical approach have been from the Homogeneous physics and math of XIX.
Especially the last author with numerous grants from the NSF and NIH is probably the mathematical motor behind the study direction, unfortunately.
The words "multiscale modeling" and "simulation of vascular tumor growth" have in common only the list of known chemical processes based phenomena associated with cancerous tumor growth, that's it.
4) All the problems with the design and implementation of this study were growing from the main premise -- is that the mathematical and physical base for the initial idea and model design is the "multiscale" while the authors obviously do not know, they lack of knowledge, what is the multiscale and heterogeneous physics and mathematics.
They just dwell in an ivory tower of old homogeneous physics and math.
5) Important is that if authors knew and applied the basics of HSP-VAT then the number of frivolous adjustable parameters would be dramatically scaled down. But equations' complexity and number would increase also dramatically.
As mathematicians they could read some research around?
Well, the polyscale model for this kind extremely complicated medicinal problem will be significantly more complex. That is the real price for improvement of quality.
=============================================================================================We will touch further few confined areas of Non-Local Two-Scale "Analysis of Current Studies on Scaled, Collective Phenomena in Medicine Fields Presented as the One-Scale Concepts" to lay down the used now in medicine homogeneous medium mathematical foundations, and then move to some extent into formulation of Non-Local Upper Scale Two-Scale (at least) "Analysis of Current Studies on Scaled, Collective Phenomena in Medicine Fields" main definitions.
These are also the well known problems - that in no way can be solved within the Homogeneous One-Scale Collective Phenomena in Medicinal Science theories.
