
 is why the collection of annotated texts is rather the freely selected one for
some reason studies, than the thorough balanced review on the topic.
is why the collection of annotated texts is rather the freely selected one for
some reason studies, than the thorough balanced review on the topic.
One of the main points in the exposition here is that we do not intend to teach or describe with detail the peculiarities of traditional theories and methods treating the scattering in Electrodynamics and Optics, but rather we need (As In Other Respected Sciences at This Website) to point out on hidden, unsolved, or untouchable themes, topics on scattering in both mentioned sciences and speak about the VAT possibilities to fill the gaps.

 is why the collection of annotated texts is rather the freely selected one for
some reason studies, than the thorough balanced review on the topic.
is why the collection of annotated texts is rather the freely selected one for
some reason studies, than the thorough balanced review on the topic.

 frankly speaking, we don't pursue here the idea to develop the wall of
indestructible arguments in our favor. We put forward the demanding issues
picture and then follow the main ideology of this website that - the VAT
Scaling Tools for Heterogeneous Media are like the Gauss-Ostrogradsky theorem
for a Homogeneous medium.
frankly speaking, we don't pursue here the idea to develop the wall of
indestructible arguments in our favor. We put forward the demanding issues
picture and then follow the main ideology of this website that - the VAT
Scaling Tools for Heterogeneous Media are like the Gauss-Ostrogradsky theorem
for a Homogeneous medium.
We will demonstrate in this subsection the few features showing that the subject is better to approach with the two- or more physical scales to theorize, model, and simulate - using the VAT, because it is the best tool at this time around.
The pretty good analysis of one scale scattering problem in linear acoustics and electrodynamics has been given in old review paper by Barabanenkov et al. (1971) and other nice researches which we discuss in the "Acoustics" section of this website -
Meanwhile, the same famous problem of wave scattering in Optics has some specifics on its own, some of them we would like to expose and discuss here.
The review paper by Flytzanis, C., Hache, F., Klein, M.C., Ricard, D., and Roussignol, Ph. (1991) concerns mostly the composites consisting of metal or semiconductor particles in a transparent dielectric matrix.
On page 323 we can read that:
''....artificial heterogeneous semiconductor-dielectric or
metal-dielectric microstructures where quantum confinement plays a central
role. The fundamental aspect is related to the long-standing
question of the validity range of crystal solid-state concepts (and behavior)
and their relation to molecular and atomic properties. This issue is essential
in the understanding and prediction of properties in crystals with extended
electronic states, like metals, semiconductors, or conjugated polymers, where
the electronic density distribution of the constituent elements undergoes
drastic modifications in the course of forming the crystal. ''...
On page 338 we read good words on collective phenomena :
''First, in the metal or semiconductor nanocrystals or microcrystals, the otherwise delocalized valence electrons in the bulk can find themselves confined in regions much smaller than their delocalization length, which is infinite in the ideal perfect metal and of the order of several tens to a hundred Ångströms in a perfect semiconductor; this drastically modifies their quantum motion as probed by optical beams but also their interaction with other degrees of freedom.
Second, because the size of the crystallites is much smaller that the wavelength and their dielectric constant is very different from that of the surrounding transparent dielectric, the electric field that acts on and polarizes the charges of these crystallites can be vastly different from the macroscopic Maxwell field. These two effects, the first quantum-mechanical and the second classical, go under the names of quantum and dielectric confinements, respectively, and are particularly conspicuous in the optical frequency range. The first requires the solution of the Schrödinger equation in a spatially confined region whose boundary conditions impose a significantly different eigenfunction and eigenenergy spectrum from those of the bulk, and the second requires introduction of the effective dielectric medium approach."
Note - What about the connection between these two - between the quantum and the dielectric confinement, at least, scale models ??
Later in that same paper authors came to talk about the effective-medium
approximation and the Maxwell-Garnett formula for effective dielectric
permittivity and of the Bruggeman's effective-medium formula
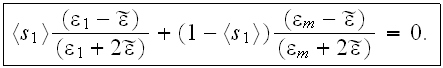
Which is the quite obsolete technique for this solid state formulated field as Nonlinear Optics in composites.
So, they did try to describe the dielectric confinement via the one scale traditional model, even referring to the "appropriate statistical averaging".
For quantum confinement authors used the Schrödinger equation
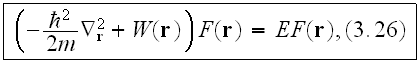
to find out confinement regimes in the spherical(?) semiconductor and metal crystallites.
Interesting enough is - How authors treat the presence of interfaces: "the
interface with the surrounding dielectric will introduce an additional
potential term W in eq. (3.29), so that the equation
for
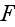 will be
will be
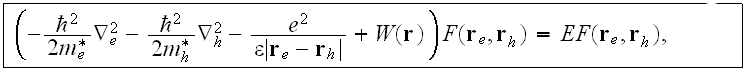
where for simplicity we will assume that

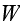 is the same as the metallic crystallites; namely,
is the same as the metallic crystallites; namely,

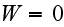 for
for

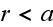 and
and

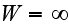 at
at

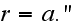 ??
??
The rest of the paper devoted to traditional one scale homogeneous physics treatment of composites, mostly offering quantum confinement procedures and discussions.
The review paper by Barabanenkov et al. (1991) devoted to Enhanced Backscattering in optics.
There is the explanation of backscattering phenomena on page 68 - "The double passage of a wave through the same inhomogeneities gives rise to the effect of backscatter enhancement (BSE)."
The text supported by Figs. 1-1 and 2-1.
While we see that the more pleasant would be the explanation based on the already known from other fields non-local effects noticeable via the Upper scale VAT GE. Also, observe the thoroughly disputed results on "Internal generation" by Pereverzev and Ufimtsev (1994) - see their figures below in the subsection -
The Fig.2-18 by authors themselves depicts the part of more realistic scattering picture in heterogeneous media -
Page 125 - "Averaging the respective expansions of

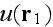 and
and

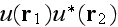 over the ensemble of realizations of the scatterers yield the Dyson and
Bethe-Salpeter equations for average field and coherence functions (Frisch
[1965[ and Finkelberg [1967])
over the ensemble of realizations of the scatterers yield the Dyson and
Bethe-Salpeter equations for average field and coherence functions (Frisch
[1965[ and Finkelberg [1967])
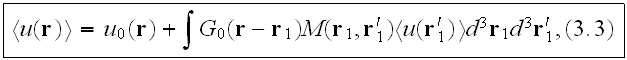
and
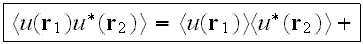
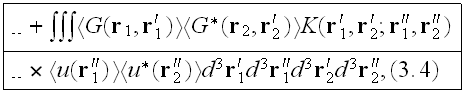
where

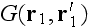 is the Green function of Helmholtz equation (3.1) having the average
is the Green function of Helmholtz equation (3.1) having the average

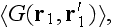 which satisfies the Dyson equation, which differs from eq. (3.3) by having
which satisfies the Dyson equation, which differs from eq. (3.3) by having

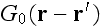 and
and

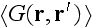 in place of
in place of

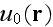 and
and

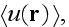 respectively."
respectively."
Page 131 - authors present the figure like REV in the scattering slab Fig. 3.3 -
for other then averaging reasons.
Page 185 - "As long as a well-developed theory of scattering from large, steep, and rough heights is unavailable, it is logical to resort to a model description of antispecular scattering." The Fig. 5.2 on this page -
illustrate the incident upon grating on the surface. We need to note only that again in the modeling in this mode thinking being involved only the one phase - an upper half-space, which is admittedly an air medium.
The body of texts in this subsection openly speaks out that the theory and methods are meant and used now for the one scale local field values. Even when problem stated as with the Dyson equation.
We see that the way of treatment in numerous, not only few works discussed above and mentioned in references, studies the methods employed - those addressing the one phase wave scattering.
But when the second phase is undeniably need to be present

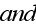

 - then, the stochastic equations are brought into the scene with the Dyson and
Bethe-Salpeter equations.
- then, the stochastic equations are brought into the scene with the Dyson and
Bethe-Salpeter equations.
References
Barabanenkov, Yu.N., Kravtsov, Yu.A., Rytov, S.M., and Tamarskiï, V.I., (1971), "Status of the Theory of Propagation of Waves in a Randomly Inhomogeneous Medium," Sov. Physics Uspekhi, Vol. 13, No. 5, pp. 551-680.
Barabanenkov, Yu.N., Kravtsov, Yu.A., Ozrin, V.D., and Saichev, A.I., (1991), "Enhanced Backscattering in Optics," chap. 2 in Progress in Optics, Vol. XXIX, E.Wolf, ed., Elsevier Science Publ., Amsterdam, pp. 64-197.
Flytzanis, C., Hache, F., Klein, M.C., Ricard, D., and Roussignol, Ph., (1991), "Nonlinear Optics in Composite Materials. 1. Semiconductors and Metal Crystallites in Dielectrics," Chap. V in Progress in Optics, Vol. XXIX, E.Wolf, ed., Elsevier Science Publ., Amsterdam, pp. 321-411.
Frisch, U., Wave Propagation in Random Media. II. Multiple Scattering by n Bodies, Institut d'Astrophysique, Paris, 1965.
Goldberger, M.L. and Watson, K.M., Collision Theory, Wiley, New York, 1964.
Gurbatov, S.N., Malakhov, A.N., and Saichev, A.I., Nonlinear Random Waves in Nondispersive Media, Manchester University Press, Manchester, 1991.
Keller, O., Nonlinear Optics in Solids, Springer-Verlag, Berlin, 1990.
Klyatskin, V.I., Stochastic Equations and Waves in Randomly Inhomogeneous Media, Nauka, Moscow, 1980.
Hutley, M.C., Diffraction Gratings, Academic Press, London, 1982.
Electromagnetic Theory of Gratings, R.Petit, ed., Springer-Verlag, Berlin, 1980.
Maystre, D., in Progres in Optics, E.Wolf., ed., Elsevier, Amsterdam, 1986.
Rytov, S.M., Kravtsov, Yu.A., and Tatarskii, V.I., Principles of Statistical Radiophysics, Vol. 3, Random Fields, Springer, Berlin, Heidelberg, 1989.
Rytov, S.M., Kravtsov, Yu.A., and Tatarskii, V.I., Principles of Statistical Radiophysics, Vol. 4, Wave Propagation Through Random Media, Springer, Berlin, Heidelberg, 1989.
Shen, Y.R., The principles of Nonlinear Optics, John Wiley & Sons, New York, 1984.
Sheng, P., ed., (1990), Scattering and Localization of Classical Waves, World Scientific, Rivers Edge, NJ.
Soukoulis, C.M., ed., (1993), Photonic Band Gaps and Localization, Plenum, New York.
Soukoulis, C.M., ed., (1996), Photonic Band Gap Materials, Kluwer Academic Publishers, Dordrecht. 729 p.
Turner, J.A. and Weaver, R.L., "Radiative Transfer of Ultrasound," J. Acoust. Soc. Amer., Vol. 96, No. 6, pp. 3654-3674, 1994.
Turner, J.A. and Weaver, R.L., "Radiative Transfer and Multiple Scattering of Diffuse Ultrasound in Polycrystalline Media," J. Acoust. Soc. Amer., Vol. 96, No. 6, pp. 3675-3683, 1994.
Ufimtsev, P.Ya., The Method of Edge Waves in the Physical Theory of Diffraction, US Air Forse, Wright-Patterson AFB, OH, 1971.
Yariv, A., Quantum Electronics, John Wiley & Sons, New York, 1975.
Yariv, A. and Yeh, P., Optical Waves in Crystals, John Wiley & Sons, New York, 1984.