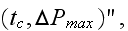Pseudo-Science of Constructal Theory (Hierarchy) in Heat Transfer Modeling
Among numerous publications (there is the website) by A.Bejan on the subject
of volumetric heat transport features, modeling and even optimization, we
might be able to include here just few of many discussed and examined mostly
in 1990s, following with few recent publications. The reason is simple - to
explain to the professional and student communities the unsatisfactory claims
on usefulness, generality and applicability of the "Constructal theory" for
the heterogeneous scaled heat transfer problems.
Again as I said in -
"Announcement #3: There is our intention in this website first of all
to serve better to this field and to people studying and working in it. The
issue of analysis of published in the field research papers, reviews, books is
the inseparable activity. That is why everybody should understand and think
about critical materials appearing on these pages - as of usual component of
healthy movement in the area.
There is no personal critique on these pages........."
There is the old starting paper on volumetric heat transfer by Bejan, A.:
"Theory of Heat Transfer From a Surface Covered with Hair,"
Trans. ASME, J. Heat Transfer, Vol. 112, pp. 662- 667,
(1990).
In p. 662 one can read that: "The objective of this paper is to describe the
fundamental heat transfer mechanism of a surface covered with hair."
The idea of the paper is good - but the mathematical models and GE (3,4), (17)
are incorrect, that unfortunately precludes any further reasonable analysis.
In the p. 665 the homogeneous Linear [W/m] heat transfer rate definition is
given. For the Heterogeneous Volumetric (or 2D as in this case) this kind of
heat transfer characteristic is inappropriate due to loss of few transport
features, see the explanation in -
and
,
where given an in-depth analysis of some two-scale thermal transport in
porous medium of surface porous layers and in heat exchangers.
The paper can be used as one of examples of - How not to treat the 2D
Heterogeneous problem. Anyway, formulation of a problem, where instead of the
total number of constituted parts missed one or more of them, will direct the
statement and solution in an insufficient territory regarding its results.
That is why; the conjugation of heat transfer two-phase problems has been
debated in 70s-80s, rather long ago. All of that is - to improve the validity
and increase the accuracy and power of solution. Well, since then we
understand the power of collective polyscale phenomena better and better, that
is why the HSP-VAT appeared on scene.
~~~~~~~~~~~~~~~~~~~~~~~~~
Bejan, A. and Sciubba, E. (1992), "The Optimal
Spacing of Parallel Plates Cooled by Forced Convection," Int.
J. Heat Mass Transfer, Vol. 35, No. 12, pp. 3259-3264.
In the study by Bejan and Sciubba (1992) authors did the problem where - the
stack of one size width

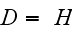 (in our notations)
(in our notations)

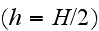 flat layers in which moves in x-direction in laminar regime a fluid has the
average fluid velocity
flat layers in which moves in x-direction in laminar regime a fluid has the
average fluid velocity

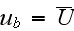
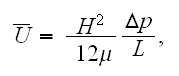
where

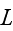 is the length of the channel,
is the length of the channel,
while the mass flow rate per slit unit width is
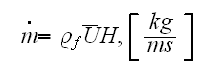
(when usual mass flow rate is

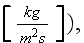 and the heat transfer rate
and the heat transfer rate

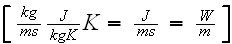 the amount of heat removed per slit unit width is
the amount of heat removed per slit unit width is
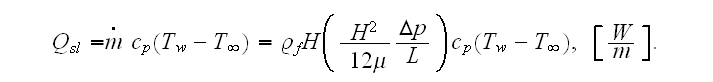
Authors give the optimal spacing (width of the channel) for developed laminar
regime in the stack of equal flat channels when the walls are heated to
constant temperature

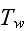 as
as
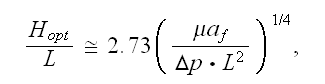
where

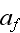 is the thermal diffusivity of the fluid.
is the thermal diffusivity of the fluid.
Also, authors created few more formulae for the case of developing flow, one
wall is at

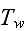 while other is adiabatic, uniform heat flux at the entrance part of the
channel. The all analysis is obtained by using the extreme transition method -
when investigated the cases of
while other is adiabatic, uniform heat flux at the entrance part of the
channel. The all analysis is obtained by using the extreme transition method -
when investigated the cases of

 and to
and to

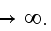
The problem stated as a
non-conjugate one.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Morega, A.M., Bejan, A. and Lee, S.W., (1995),
"Free Stream Cooling of a Stack of Parallel Plates," Int. J.
Heat Mass Transfer, Vol. 38, No. 3, pp. 519-531.
Morega et al., (1995) did the work based on the numerical solution of the free
convection problem over a number of (vertical) plates attached to a surface.
The problem stated as a
non-conjugate one.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The work by Rocha, L.A.O. and Bejan, A., "Geometric Optimization of Periodic
Flow and Heat Transfer in a Volume Cooled by Parallel Tubes,"
J. Heat Transfer, Vol. 123, No.2, pp.
233-239, (2001).
This is the good article for comparison and for criticism on the approach
followed by Bejan,
which here was done for the "non-conjugate"
problem, which instantly deprive any sense to talk about optimization,
- because authors have just thrown away the second phase !!
In p. 233 from the abstract one can read that - "This paper addresses the
fundamental problem of maximizing the thermal contact between an entire
heat-generating volume and a pulsating stream of coolant that bathes the
volume. The coolant flows through an array of round and equidistant tubes. Two
laminar flow configurations are considered: stop-and go flow, where the
reservoir of coolant is on one side of the volume, and back-and forth flow,
where the volume is sandwiched between two reservoirs of coolant. The total
heat transfer rate between the volume and the coolant is determined
numerically for many geometric configurations in the pressure drop number
range

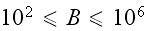 ,
and
,
and

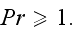 "
"
How dare authors saying about heat transport "between the volume and
the coolant" - if the study does not have a solid phase in the
problem!
Also in the p. 233 authors refer mostly to the Bejan's own studies - where:
"The most recent constructal work dedicated to compact heat exchanger and the
cooling of electronic packages has focused attention on
geometry - how shapes and structures can be designed
so that a global performance objective is met subject to global constraints
[1]." - this is reference to the Bejan's (2000) book.
"Examples that come closer to the geometric optimization, that spacing between
heat generating components are optimized, so that the given volume is used to
its fullest."
That is the stretching - No one ever and up to now can tell
that the Volumetric Heterogeneous Heat Transfer Optimization achieved. Not in
a Single instance.
p. 234 - given the equation for the fluid phase - inside the tube as (eq. (4))
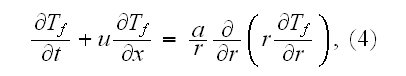
"where

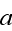 is the thermal diffusivity of the fluid. There are the three boundary
conditions:
is the thermal diffusivity of the fluid. There are the three boundary
conditions:
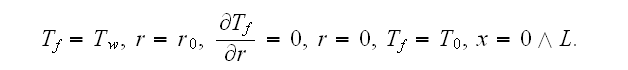
The fluid flow statement corresponds to
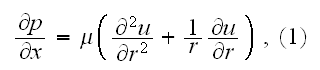
which is the usual laminar flow equation with the solution
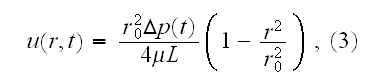
They have not the heat transfer rate per unit volume
- but rather the "unit of duct volume" which is not used and known unity for
heat transfer.
In p. 234: "The quality of interest is the average heat transfer rate per
unit of duct volume use."
Noting - "per unit of duct volume use"? Is it cooled the solid or the fluid
"duct volume"?
Doing this definition, on p. 235 "the average heat transfer rate per unit
volume" introduced
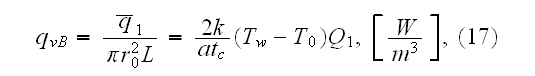
where

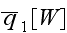 is the time-averaged "heat transfer rate" in their definition and in units
is the time-averaged "heat transfer rate" in their definition and in units

![$\left[ W\right] $](/thermph/pic/PseudoH__25.gif) ,
,

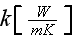 is the fluid's thermal conductivity,
is the fluid's thermal conductivity,

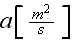 is the thermal diffusivity (of fluid),
is the thermal diffusivity (of fluid),

 is the time period
is the time period

![$\left[ s\right] $](/thermph/pic/PseudoH__29.gif) ,
and
,
and

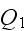 is the dimensionless integral of temperature gradient integrated over the tube
wall and over the time period.
is the dimensionless integral of temperature gradient integrated over the tube
wall and over the time period.
Authors later, on p. 235 (expr. (27)) also give the real volumetric flux "heat
transfer rate per unit volume" of medium
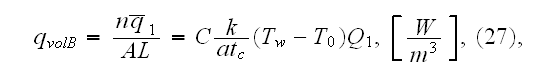
where

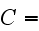

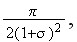

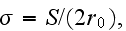 and
and

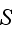 is the spacing between adjacent tubes
is the spacing between adjacent tubes

![$\left[ m\right] $](/thermph/pic/PseudoH__36.gif) .
.
So, according to dimensions, this is not a "heat transfer rate per unit
volume" - this is the volumetric heat flux in general, as for the same reasons
the meaning of the HSP-VAT variable
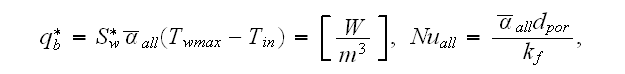
using which we can compare the current set up with the correct conjugate
volumetric flux following the VAT developments for the straight stochastic
diameter pore capillary morphology medium (see the definitions and explanation
in
as this volumetric flux is
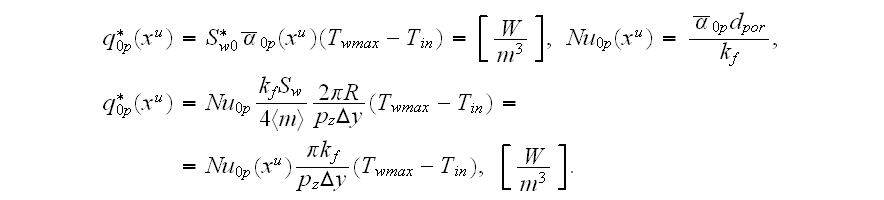
The value

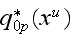 would be expected significantly different from the
would be expected significantly different from the

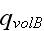 because
because

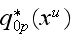 obtained following the solution of the conjugate problem - meaning the
two-phase problem.
obtained following the solution of the conjugate problem - meaning the
two-phase problem.
Let's explore in more detail what is meant by Bejan and co-authors when the
"volumetric cooling" terms made use of?
In this and other papers (works) by Bejan and co-authors he considers - as for
the "Modeling and Optimization" in the heat transfer solid-fluid systems ONLY
the Fluid system's phenomena? Non-conjugate models and mathematical statements
used.
How it can be told that the heat transfer problem and Optimization is sought
and performed, when the solid phase temperature or heat flux are fixed?
It's out of a good reasoning; it's the pseudo-science at present time. Well,
30-40 years ago when no mathematical tooling and computers mostly were
utilized that might constitute the advancement, but not nowadays.
It's said - the "duct volume," and at the same time authors saying - "..in a
volume cooled parallel tubes.."
Well, then this is the pseudo-statement and pseudo-claim on the distributed
heat transfer "optimization".
There is no such thing as to "optimize" the volume process and discard at the
same time the part of the said volume completely.
When one can read further in the p. 235 that - "In other words, the geometric
maximization of

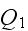 teaches us how to select the dimensions of the tube bundle so that the entire
volume
teaches us how to select the dimensions of the tube bundle so that the entire
volume

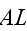 is reached most effectively by the fluid when the pressure cycle is specified
is reached most effectively by the fluid when the pressure cycle is specified

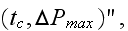
we would surely say - this is just conventional homogeneous heat transfer
statement for quite different task that can not be covered by the one scale
local physics concepts.
Also, one would think
again that the problem is about the "entire volume" heat dissipation rate
optimization?
And will be wrong, there is the trick here with substitution of one real thing
- the total volume where a heat dissipates, by the one phase only volume -
which is the very simple physics disconnected from the other phase.
Also, the approach demonstrated by Rocha and Bejan (2001) won't allow to
consider the problem with the irregular or distributed diameters of pores (and
any other heat transfer elements in other similar publications). Because again
- one needs to average over the space (and in time, if needed) the heat
transfer characteristics while applying this principle. And they can not do
that within this approach.
See more features on Volumetric Heat Transfer Device (VHTD) modeling in our -
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Closer to our times - one can see more on how this conceptual description of
the pseudo-science of "Constructal Theory" works for the Volumetric Flow and
Heat exchange.
Lorente, S., and Bejan, A., "Heterogeneous porous media as multiscale
structures for maximum flow access," J. Appl. Phys.,
Vol. 100, pp. 114909-1- 114909-8, (2006).
We can read from the abstract:
"We develop completely multiscale configurations that guide the flow from one
side of the porous structure to the other line to line and plane to plane and
show analytically the advantages of tree structures over the usual stacks of
parallel microchannels. The "porous medium" that has tree-shaped labyrinths is
heterogeneous, with multiple scales that are distributed nonuniformly."
Our comment: Well, we see now the word "multiscale" appeared
in the texts! So what? What does this mean -- constructing the graph
figures?
Those figures are not connected to a scaled physics --
because each element is constituted, thought and modeled as a Lower scale only
the simplified physics physical and mathematical model.
No path to go to generalization of the Upper scale because
there is no theory for the Upper scale mathematics, physics and
modeling!
p. 114909-5: "Although the structure of Fig. 5 is marginally less
permeable this is another confirmation of the earlier work
done on trees, Figs. 2 and 3, Fig. 5 is simpler than Fig. 1. It
has fewer channels: this is an attractive feature for the design
of microchannel structures."
So, what? These figures we drew in 1992-93 and found that
this way of doing scale construction and communication is going to the
dead-end without the second Upper scale consideration -
Because, there is no way by childish drawings to develop,
design, model and simulate the network of pores, tubes as the finite set of
elements and to raise the physics and theoretical generalization to the Upper
scale.
There should be the way to figure out the Upper scale physics and mathematics
tight to these drawings in a meaningful way - as the HSP-VAT does.
2) For the round tubes the equations (7) -- (18) have no
sense to model and simulate unless we have the tools, mathematics, models to
make the generalization of those calculations.
Which only the HSP-VAT has and demonstrated with problems and
models solved.
About Figs. (1)-(5) in the paper; I have created numerous
figures like that for purposes to model and simulate the lower network scale
flow process and fields. But I did that freely because I had the tools to
obtain the data reduction, the data analysis for understanding --How flow is
going on and how morphology affects the flow rate and pressure drop at the
Upper (averaged fields) scale.
This is not possible with the one scale modeling by
"constructal" theory!
Besides, and this is quite important thing -- the HSP-VAT
gives the ability to see the second scale physical effects (phenomena- as we
found in the direct modeling of those additional integral and
integro-differential terms) -- that the "constructal" theory is not able to
deliver, to detect, show up, or model!
3) The same in many similar graphs of flow in porous media
for the Lower scale description in HSP-VAT we had drawn in 1992-94 and
presented in the proposal for the DOE grant at UCLA.
The reasons for our exercises in drawing were different --
that were the methods of the Lower scale depiction and simulation with the
imperative aim to seek and solve the Upper scale momentum transport in porous
media.
This is the real Goal of all these constructions, not to draw
the figures for qualitative reasoning on their qualities.
p. 114909-5: "The opportunity to discover the best architecture of a
point-to-plane tree is illustrated by the following analysis of the construct of Fig. 7."
Our comment -- There is no opportunity to discover anything
with this approach as soon as just the mechanistic connection of the tubes
(pores) (without nodes specific characteristics as pressure drop and flow
turbulence) does not create the model to analyze the physical process of flow
in that network as a whole for the Upper scale processes. Hydraulic estimation
is used in the Hydrology for long ago -- still nobody (but Bejan) would claim
that the hydraulic network calculation creates the new level of generality for
better understanding and design of a pipe flow network as a porous
medium.
Also, again -- there are a number of physical effects that
the Lower scale pipe network simulation can not discover and include in
modeling and data reduction for the Upper physics scale.
In Conclusions p. 114909-7 one can read:
"The observer who looks from the outside at the side of the porous medium
e.g., from the top of Figs. 1 and 6 sees a few large pores surrounded by many
small pores. From this viewing position, the porous medium appears to have two
scales."
Our comment -- Really? Oh, now at last, authors can see the
two scales in porous medium that was obvious from the beginning.
Unfortunately, there are also the two-phase media and the 3-scale distinct
means to model the process of fluid flow.
Does the "constructal" theory, this the one scale method of
graph description of flow in porous media able to deliver the solution of any
(one) classical problem in fluid mechanics of porous media? As the HSP-VAT
does -
Of course, not.
Can this "constructal" theory to deliver the effective
transport coefficients for fluid mechanics of porous media? As the HSP-VAT
does -
Of course, not.
Can this "constructal" theory deliver the transport problem
solutions in fluid mechanics of porous media, as in the soil and groundwater
contamination science, for example? As the HSP-VAT does -
and
Of course, not.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Dai, W., Bejan, A., Tang, X., Zhang, L., and Nassar, R., "Optimal temperature
distribution in a three dimensional triple-layered skin structure with
embedded vasculature," J. Appl. Phys., Vol. 99, pp. 104702-1- 104702-9,
(2006).
In p. 104702-2 we can read that: "Here, the dimension and blood flow of
multilevel blood vessels are determined based on the constructal theory of
multiscale tree-shaped heat
exchangers.
 "
"
Our comments: This is the pretty obsolete and incorrectly
stated homogeneous model for the blood distribution and heat transport in
human tissue. For example, and that is the main error:
The basic initial statement equations (4) --(7) are not
matching one to another -- meaning the first three supposed to be matching to
the last one -- (7). And the first three -- are supposed to interface in a
meaningful way between themselves -- not using the algebraic terms assignment.
Authors can not develop the models of heat transfer in the
three scale blood network imbedded into tissue, tumor's tissue!
Their model -- Bejan's based "constructal" model, is just
hand glued singled out lower scale homogeneous equations with no ability to
get the local-non-local averaged model and its mathematical statement for this
task.
Among the few first coming questions after reading this paper we can ask:
2) Does the "constructal" theory, this one scale method of graph description
of heat transport and flow in porous media -- human tissue (that is much more
complicated); able to deliver the modeling and solution of any (one)
reasonably stated problem of the heat transfer in human tissue, tissue model?
Remember, this is the polyscale media and physical processes. As the HSP-VAT
does -
and
Of course, not.
Is the "constructal" theory able to deliver the solution of any (one)
classical problem in Thermal Physics of porous media? As the HSP-VAT does -
Of course, not.
Can this "constructal" theory do deliver the effective transport coefficients
within Thermal Physics of porous media? Which we need for the intermediate and
preliminary results tissue modeling. As the HSP-VAT does -
Of course, not.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Bejan, A. and Lorente, S., "Constructal theory of generation of configuration
in nature and engineering," J. Appl. Phys., Vol. 100, pp. 041301-1- 041301-27,
(2006).
From the p. 041301-1: "This principle was formulated in 1996 as the
constructal law of the generation of flow configuration.1--5 "For a flow
system to persist in time to survive it must evolve in such a way that it
provides easier and easier access to the currents that flow through it."
Also from the abstract: ". The same principle yields new designs for
electronics, fuel cells, and tree networks for transport of people, goods, and
information."
Our comments: There is the law in an equally (as the
"constructal" theory) great science as the philosophy and it says:
"The sufficient amount of something (entity, events, matter,
etc.) would inevitably transfer the means and values of that "something" to
another qualitative state, another quality of a subject."
The Law of Quantity-to-Quality transfer.
That means the few facts with the mechanical simple
observation as we might find in the "constructal" theory, is not qualified to
be the next scale generalization ground breaking theory!
That would be careful to say
-- that the general observation is not yet a scientific conclusion, not a
worthwhile ground for claiming a World actuality discovery and so on.
In the p. 041301-16 we can read: "Optimal spacings
have been determined for several configurations, depending
on the shape of the heat transfer surface that is distributed
through the volume: stacks of parallel plates e.g., Fig. 20,
bundles of cylinders in crossflow, arrays of staggered plates,
and arrays of pins with impinging flow."
Our comments - These are the same arguments we dealt with in
the above mentioned and analyzed studies by Bejan on the "constructal" theory
applied to the heat transport!
Read the above notes.
This is not a science -- it is the system of desires, the
theological system.
In page 041301-25 : "In summary, the body of work reviewed for the first time
in this article introduces a paradigm that is universally applicable in
natural sciences physics and biology, engineering, and social sciences."
Well, that kind is familiar from the history -- this is the
self-appointment for everything without a limit!
This claim is for a "law" of universality and greatness.
In the whole text we could not find some original reasonable
scientific arguments -- apart of simplistic geometric observations, like the
famous allometric laws in biology. Which we have noted is an analog of Darcy
law in Fluid Mechanics and really should be greatly advanced when applied to field problems.
For all the more strict comparisons and mathematically
strict modeling quality we just spoke in our above remarks on the studies with
the words "constructal" theory in texts, and in other parts of this website.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Why Bejan continues to do this kind of claims well over more than 18 years?
Our guess would be that in spite the correct words Bejan writes - "The
optimization proceeds in a series of volume subsystems of increasing sizes
(elemental volume, first construct, second construct. The shape of the volume
and the relative thicknesses of the fins are optimized at each level of
assembly"
- in reality he can not do neither the each scale correct modeling, nor the
connection between each of the two (at least) neighboring scale models.
Summarizing the above
said features about this approach to the heat transfer modeling - the
"Constructal theory" we can enumerate the mortal highlights of it:
1) Not included the second of at least, phase for modeling and optimization.
2) Not included the physical phenomena of the two-phase scaled transport. It's just
not possible to do that.
It is not even possible because this formula of operation - the concept for
the phenomena does not allow involving the other then the homogeneous
mathematical statements for a one phase modeling.
3) There is the wrong understanding and modeling mathematical statements as
long as the GE's (governing equations) are used at the Lower (local) scale
phenomena while the heat transfer design and optimization goals have taken for
the Upper scale phenomena (those should be averaged, but they are not) - as
the heat transfer rate, etc.
4) But the most important is that the HSP-VAT statement gives possibilities to model and
calculate the really hidden components of the heat transfer, those are not
seen in the "constructal" theory works with homogeneous mathematical
statements for heterogeneous scaled problems.
5) The two-scale local-non-local VAT formulation of Heterogeneous,
Hierarchical heat transfer problems have additional terms on the Upper scale.
These are reflecting the additional physical phenomena which physically known,
but can not be observed via the modeling through the one-scale homogeneous
models.
Otherwise, the scaled VAT formulation allows one to include and study the
phenomena for the Upper scale that are not observable when conventional
homogeneous modeling is used.
Among these features in Heterogeneous Scaled Heat Transfer are:
5.1) the heat transport due to the
interface surface (could be a few percent of the overall rate for HE
processes);
5.2) an exact description of interphase transport and its connection to
the morphology (could be 20% or more);
5.3) field interaction based heat transport
(as driven by fluctuations in temperature and in fluid velocity (could be as
much as 10%));
5.4) and nonlinearities resulting from physical models and their
coefficients and forces interacting one with another.
5.5) The VAT based averaged
Upper scale heat sink heat transfer parameters are vector and tensor variables
tied directly to the each phase performance -
6) There is the slogan in the HSP-VAT:
"There exists no way to find out, to control or to optimize the performance of
the two- or three scale volumetric heat transfer device (VHTD) while using the
only Lower Scale modeling equations."
REFERENCES:
Bejan, A., "Theory of Heat Transfer From a Surface Covered with Hair,"
Trans. ASME, J. Heat Transfer, Vol. 112, pp. 662- 667,
(1990).
Bejan, A. and Sciubba, E., "The Optimal Spacing of Parallel Plates Cooled by
Forced Convection," Int. J. Heat Mass Transfer, Vol.
35, No. 12, pp. 3259-3264, 1992.
Bejan, A. and Morega, A.M., "Optimal Arrays of Pin Fins and Plate Fins in
Laminar Forced Convection," J. Heat Transfer, Vol. 115, pp. 75-81, 1993.
Bejan, A., "The Optimal Spacing for Cylinders in Crossflow Forced Convection,"
J. Heat Transfer, Vol. 117, pp. 767-770, 1995.
Morega, A.M., Bejan, A. and Lee, S.W., "Free Stream Cooling of a Stack of
Parallel Plates," Int. J. Heat Mass Transfer, Vol. 38,
No. 3, pp. 519-531, 1995.
Ledezma, G., Morega, A.M., and Bejan, A., "Optimal Spacing Between Pin Fins
with Impinging Flow," Journal of Heat Transfer, Vol.
118, pp. 570-577, 1996.
Bejan, A., "Constructal Trees of Convective Fins," Journal of
Heat Transfer, Vol. 121, pp. 675-682, 1999.
Bejan, A., Shape and Structure: From Engineering to
Nature, Cambridge U. Press, Cambridge, (2000), and references therein.
Rocha, L.A.O. and Bejan, A., "Geometric Optimization of Periodic Flow and Heat
Transfer in a Volume Cooled by Parallel Tubes," J. Heat
Transfer, Vol. 123, No.2, pp. 233-239, (2001).
Dai, W., Bejan, A., Tang, X., Zhang, L., and Nassar, R., "Optimal temperature
distribution in a three dimensional triple-layered skin structure with
embedded vasculature," J. Appl. Phys., Vol. 99, pp.
104702-1- 104702-9, (2006).
Bejan, A. and Lorente, S., "Constructal theory of generation of configuration
in nature and engineering," J. Appl. Phys., Vol. 100,
pp. 041301-1- 041301-27, (2006).
Lorente, S., and Bejan, A., "Heterogeneous porous media as multiscale
structures for maximum flow access," J. Appl. Phys.,
Vol. 100, pp. 114909-1- 114909-8, (2006).
Under Editing


Copyright © 2001...Wednesday, 02-Jul-2025 02:13:51 GMT V.S.Travkin, Hierarchical Scaled Physics and Technologies™

 (in our notations)
(in our notations)

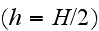 flat layers in which moves in x-direction in laminar regime a fluid has the
average fluid velocity
flat layers in which moves in x-direction in laminar regime a fluid has the
average fluid velocity

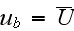
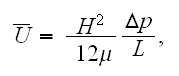

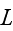 is the length of the channel,
is the length of the channel,
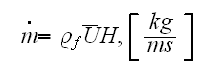

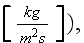 and the heat transfer rate
and the heat transfer rate

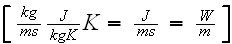 the amount of heat removed per slit unit width is
the amount of heat removed per slit unit width is
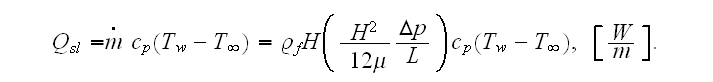

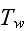 as
as
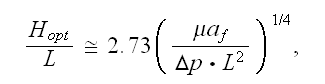

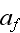 is the thermal diffusivity of the fluid.
is the thermal diffusivity of the fluid.

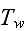 while other is adiabatic, uniform heat flux at the entrance part of the
channel. The all analysis is obtained by using the extreme transition method -
when investigated the cases of
while other is adiabatic, uniform heat flux at the entrance part of the
channel. The all analysis is obtained by using the extreme transition method -
when investigated the cases of

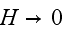 and to
and to

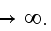

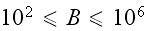 ,
and
,
and

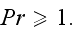 "
"
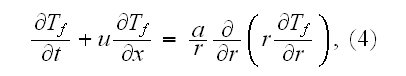

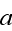 is the thermal diffusivity of the fluid. There are the three boundary
conditions:
is the thermal diffusivity of the fluid. There are the three boundary
conditions:
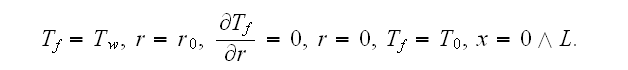
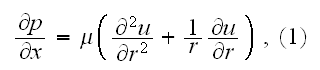
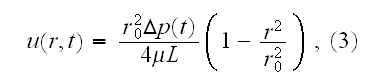
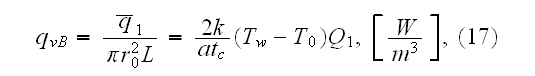

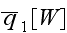 is the time-averaged "heat transfer rate" in their definition and in units
is the time-averaged "heat transfer rate" in their definition and in units

![$\left[ W\right] $](/thermph/pic/PseudoH__25.gif) ,
,

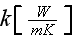 is the fluid's thermal conductivity,
is the fluid's thermal conductivity,

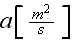 is the thermal diffusivity (of fluid),
is the thermal diffusivity (of fluid),

 is the time period
is the time period

![$\left[ s\right] $](/thermph/pic/PseudoH__29.gif) ,
and
,
and

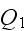 is the dimensionless integral of temperature gradient integrated over the tube
wall and over the time period.
is the dimensionless integral of temperature gradient integrated over the tube
wall and over the time period.
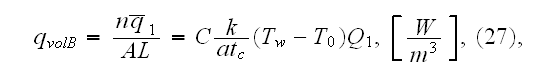

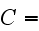

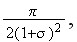

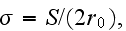 and
and

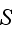 is the spacing between adjacent tubes
is the spacing between adjacent tubes

![$\left[ m\right] $](/thermph/pic/PseudoH__36.gif) .
.
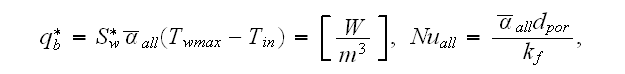
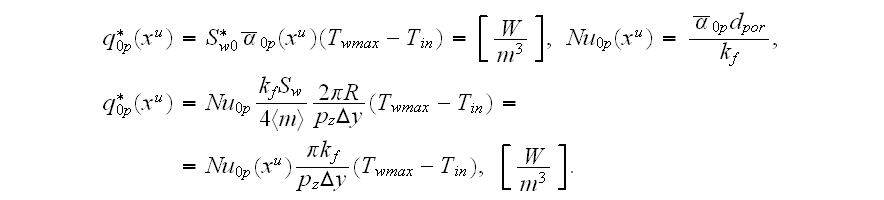

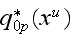 would be expected significantly different from the
would be expected significantly different from the

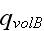 because
because

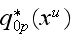 obtained following the solution of the conjugate problem - meaning the
two-phase problem.
obtained following the solution of the conjugate problem - meaning the
two-phase problem.

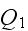 teaches us how to select the dimensions of the tube bundle so that the entire
volume
teaches us how to select the dimensions of the tube bundle so that the entire
volume

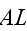 is reached most effectively by the fluid when the pressure cycle is specified
is reached most effectively by the fluid when the pressure cycle is specified