
The Annals of Frontier and Exploratory Science
INTRODUCTION
HOMOGENEOUS THERMAL PHYSICS (CONVENTIONAL) METHODS USED FOR ASSESSMENT OF HEAT SINK PERFORMANCE AND COMPARISON
HETEROGENEOUS HSP-VAT ELEMENTS BASED ONE PHASE ANALYSIS OF SEMICONDUCTOR HEAT SINK EXPERIMENTAL DATA FOR TWO MORPHOLOGIES OF SEMICONDUCTOR HEAT SINKS
RESULTS OF ONE PHASE EXPERIMENTAL DATA REDUCTION FOR TWO MORPHOLOGIES OF HEAT SINKS
HETEROGENEOUS TWO-SCALE TWO-PHASE VAT ANALYSIS OF SEMICONDUCTOR HEAT SINKS AND AN ATTEMPT TO CONNECT TO THE EXPERIMENTAL DATA
CONCLUSIONS TO THE ANALYSIS OF MEASUREMENT OF SEPARATED HEAT TRANSFER RATES FOR THE PIN FINS SHS AND FOR THE "R" SHS
SOME OF THE CONCLUSIONS TO ANALYSIS OF THE TWO-SCALE DMM-DNM SIMULATION VALUES OF SEPARATE HEAT TRANSFER PERFORMANCE CHARACTERISTICS (RATES) FOR THE LONGITUDINAL FINS SHS
AFTERMATH OF 1998-2002 STUDIES
NOMENCLATURE
REFERENCES
All of the texts given in this "Thermal Physics" section could be more I hope educating, if we focus here in this subsection ( as we strived to do in the above other subsections) our attention onto the one more real example of the HSP-VAT application, the great and demanding technologically based area of Semiconductor Coolers. In spite of the all the texts, descriptions, HSP-VAT models and solutions distributed in various places of this section - "Thermal Physics," and other sections-sciences, we try here to be more detailed and precise in the formulation of these problems - problems of the Two-Scale models devised and solutions achieved, available, and suggested in the public or proprietary domains.
One of the most applicable areas we have been considering and studying during many years is the area of special kind HE - Semiconductor Heat Sinks (SHS) with interesting and urgent topics of semiconductor devices cooling.
While in the long ago passed years of easy-happy Semiconductor Heat Sinks solutions, those were practically of the single uniform design as, for example, this one for the 486X chipset from the early 90-th

those, meanwhile, were to be replaced because of SHS surely steady heat release increase by the more sophisticated, still of the same uniform longitudinal fins designs as the following




The continuous more and more stiff and demanding interest in the heat produced evacuated from the electronic device's plate more effectively brought up the newer styles for SHS -
with designed forced convection along the short fins

or guided directed air flux down the longitudinal fins

as well as with the combined two kinds of the pin fins in the heat spreading design

finalized with some curious paired videocard-motherboard designs as this one

And, of course, these designs are not the justified scaled designs.
These four last pictures of heat exchanging solutions above are available here due to cordial permission from the editorial staff of the "XS Magazine."
In some of our works were shown the features, the extend to which the two methodology used for this kind of problems - Homogeneous One Scale and Heterogeneous Two- and more Scales HSP-VAT, and simplified VAT can be unified, compared and integrated.
There is really no contradiction between the both sciences - it is the one which extends the capabilities of another. Any reader can reach out our publications explaining in some detail how this works on both scales in texts and publications below.
The great challenge during the last ~ 15 years in semiconductor industry is the cooling to an acceptable level the heat generating electronic units. In spite that tens of millions of dollars (possible even more then that) spent by industry and by the US government for this task the results are not convincing. The greater power dissipated by the larger cooling sinks and the entire goal being attained mostly by trial and experimentation methods.
Increasing pressure to deal with a problem on a more consistent basis brought in a great effort by different government agencies.
The project in which for the first time the methodology based on the HSP-VAT was applied to tackle the heat sink design problems was launched in 1998 by the Defense Advanced Research Projects Agency (DARPA). In a large scale project with budget exceeding 10M there was the part devoted to design of the last and possibly the most heat resistive stage of electronic cooling - an air cooled heat sink -
UCLA_MOMS_HERETIC (1)-only_task_4 (2.9M)
In this part my responsibility was to develop the preliminary design procedures for scaled heat sink model, and simulate the heat transfer as for the 2 scale device. As usual in these tasks there were not enough human and financial resources. The scaled problems demanding much more in terms of resources as long as these are the large by itself tasks. The product demands more effort, more skills, more resources. Nobody up to that task approached the scaled problem of such complexity just in terms of work, not saying that there were no examples of that kind of problems tackled, and solved in HSP-VAT.
To that task, besides the lab's grad students, I attract some international forces from Russian Federation with experinces in turbulent modeling and simulation.
There were few stages in VAT application during the project -
One at the beginning
when the methodology of experiment was not known and we proceeded with the
simplified methods of two scale VAT simulation to develop the basis for physical experiment
3D round pins morphology
The history of semiconductor heat sinks design (as the part of the more general topic of heat exchangers) might suggest the questions of reliability and adequacy of basic concepts. This idea comes into mind because of the length of the studies for heat exchangers (almost as of the turbulent theory). Through the last approximately 30 years the principles of modeling and design had been advanced from a single pin simulation to the methods of heat transfer resistance for arrays of pins. It is interesting, nevertheless, as it seems that no single design was claimed as the best solution for the given conditions of temperature difference (drop) and ambient air influx.
The first step was to study fundamentals of heat enhancing surfaces (2D-3D heat sinks). The device, a heat sink (Volumetric Heat Dissipating Device - VHDD), is a spatial structure that has been designed and manufactured as a spatial structure for a reason, and the features determining its performance are, by their nature, of a spatial character. Nevertheless, today's homogeneous heat transfer models, even when conjugate problems are addressed, treat a complex interactive problem as a single scale problem with all the parameters of the morphology entering into the mathematical formulation as external assigned parameters. Often the parameters are the result of various unsatisfactory attempts for connecting heat fluxes and volumetric variables found from direct numerical simulation. In contrast, the parameters and variables arising in HSP-VAT two-scale models do not appear in the lower scale homogeneous mathematical problem formulations. They pop-up in the bulk, mean, or somehow averaged Upper scale VAT mathematical statements.
The primary intend and goal to achieve in semiconductor heat sink design is simple. It is to increase the heat transfer while decreasing the momentum resistance as is the goal for most of heat exchange devices.
Nevertheless, as soon as everyone agrees that the best way to achieve the maximum heat transfer rate within an outlined volume of heat sink is through the introduction of additional heat exchanging elements, as ribs, pins of different shape, the problem becomes a two scale heterogeneous volumetric heat exchanger design. The processes on the lower scale heat transport - in and around of a single transfer element (rib, fin) are no longer describe the heat transfer rate of the whole sink.
At the same time, the formulation of the problem for the heat sink as for the one-temperature, or even two-temperature homogeneous medium does not involve or connect the local (lower scale) transport characteristics, determined by the morphology of elements, directly to the performance of heat sink. It does not explain also - how to improve the performance characteristics?
We name here the Upper scale of the device the spatial scale which is usually corresponds to one of the device' sizes. The semiconductor heat sink has three sizes of the scale ~0(10cm), also the properties of the device performance as heat transfer rate or efficiency are related to or considered at as of the upper scale.
In our effort to tie the experimental characteristics of heat sink to the theoretical scaled (VAT) description and simulation of semiconductor base-to-air heat sink, we came to the process of coupling of two scale modeling and experiment for heat sink design.
Most past work was focused on the quasi-upper scale performance characteristics resulting in many efforts to measure the bulk heat transport rate and in modeling of numerous morphologies (see, for example, Andrews and Fletcher (1996), Bejan and Morega, (1993); Bejan, (1995); Fabbri (1999); Jubran, Hamdan, and Abdualh (1993); Kim and Kim (1999); You and Chang (1997), etc.).
In many cases experimental data reduced to the level of homogeneous device
effectiveness
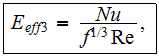 where
where

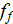 is the momentum resistance in the volume, and
is the momentum resistance in the volume, and

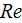 can be constructed using various variables.
can be constructed using various variables.
Meanwhile, in the two scale VAT upper scale governing equations applicable to the problem, there are four additional descriptive terms in the momentum equation (for 1D turbulent equation), seven terms in the fluid temperature equation, and five additional terms in the solid phase (reflecting heat transport through ribs, pins) temperature equations ( Gratton et al. 1996; Travkin et al., 2000).
Analysis of known methods for determination of effective transport parameters and criteria were developed for the thermal effectiveness of a heterogeneous device or medium in 90th and published in -Travkin and Catton, 2001; Travkin et al., 1998; Travkin et al., 2001a; Travkin 2001. These criteria are not the same as ones used for homogeneous devices and processes and consequently have the features of heterogeneous transport explicitly included as the medium morphology characteristics, for example.
Particularly aimed for developing procedures for the purpose of experimental closure or verification of HSP-VAT heat exchangers governing equations.
Contrary to the simulation numerical experiment the physical experiment usually much more restrictive in terms of the number of local experimental points assigned for the measurements. It is the problem to include properly those local measurements and at the same time, to assign those points of measurements within the volume of heat exchange and to the HSP-VAT data reduction procedures.
Comparisons with homogeneous criteria of performance and the consequences of effect by different mechanisms were performed further.
There are number of studies (mathematical models and experimental works) with
regard to what are the goals to achieve and tools to use while searching for
improvements or optimization of semiconductor heat sinks. The one ground
feature which used implicitly (and doubtlessly) in these researches is that
the device (heat sink) is assumed to be the subject without any specific
internal characteristics while the bulk characteristics considered. Thus, the
well used and regarded criterium of effectiveness as
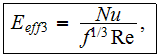 is the parameter in which the influence of heat sink morphology factors
becomes unavailable for analysis and unknown to designer. Of coarse, these
parameters are present implicitly in each of numbers
is the parameter in which the influence of heat sink morphology factors
becomes unavailable for analysis and unknown to designer. Of coarse, these
parameters are present implicitly in each of numbers

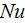 ,
,

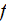 ,
and
,
and

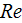 .
The point is that the goal of designer is not to find out the heat and
momentum transport characteristics of unknown device, but to design the device
(its geometrical parameters) first and then optimize its performance using
morphological parameters.
.
The point is that the goal of designer is not to find out the heat and
momentum transport characteristics of unknown device, but to design the device
(its geometrical parameters) first and then optimize its performance using
morphological parameters.
We analyze many effectiveness models used, for example, by Andrews and Fletcher (1996), You and Chang (1997), Fabbri (1999), among others, in effort to reveal the positive features in them.
Andrews, M.J. and Fletcher, L.S. (1996), provide the comparison of wide
variety of heat enhancing technologies based on the parameter of heat transfer
rate per unit volume per unit temperature difference

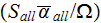 and pumping power per unit volume
and pumping power per unit volume

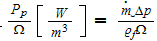 .
.
You and Chang (1997) calculated the local Nusselt number for the flat channel
with rectangular pin fins via
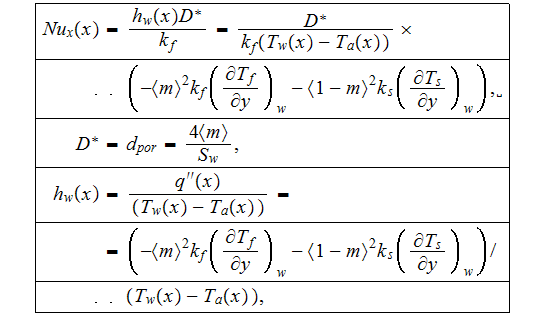
where

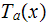 is the averaged over vertical coordinate (y) mass flow temperature
is the averaged over vertical coordinate (y) mass flow temperature
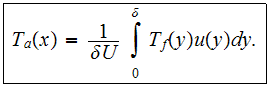 Then they averaged local
Then they averaged local

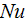 over the lenght of the sample
over the lenght of the sample
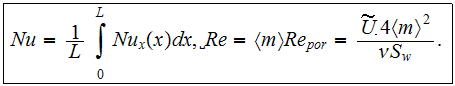
This Nusselt number is not really internal surface

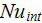 ,
because the flux determined via heat transport in both phases.
,
because the flux determined via heat transport in both phases.
Among results You and Chang (1997) obtained there is the note on p. 842 that states:
"It should be noted that the Nusselt number is not dependent on the applied wall heat flux."
Fabbri (1999) calculated for the laminar regime

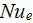 (equivalent) number in the flat channel with longitudinal rib fins as
following
(equivalent) number in the flat channel with longitudinal rib fins as
following
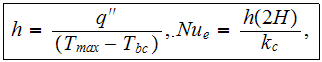 where
where

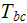 is the bulk temperature of the coolant,
is the bulk temperature of the coolant,

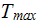 is the maximum temperature of the wall; and
is the maximum temperature of the wall; and

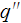 is the heat flux per unit of surface uniformly imposed on the flat side of the
finned plate
is the heat flux per unit of surface uniformly imposed on the flat side of the
finned plate

![$[W/m^{2}],$](071-3__21.gif)

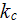 is the coolant's coefficient of conductivity. The effectiveness of the fins
morphology is considered as the variable
is the coolant's coefficient of conductivity. The effectiveness of the fins
morphology is considered as the variable
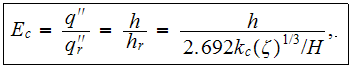 and
and

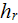 is the global heat transfer coefficient of the reference flat bottom
plate with the same hydraulic resistance
is the global heat transfer coefficient of the reference flat bottom
plate with the same hydraulic resistance

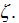 Also, the normalized hydraulic resistance
Also, the normalized hydraulic resistance

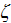 defined by author as
defined by author as
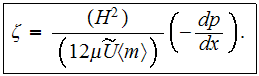 We used to compare and have discussed the weak information benefits while in
data analysis used the Nusselt numbers for comparison of different heat
dissipation devices.
We used to compare and have discussed the weak information benefits while in
data analysis used the Nusselt numbers for comparison of different heat
dissipation devices.
Our own development, using the heterogeneous media simplified performance characteristics, as:
a) heat transfer rate per unit volume per unit temperature difference

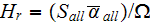

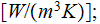 where
where

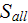 is the internal surface,
is the internal surface,

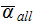 is the combined (averaged over the all internal surfaces) heat transfer
coefficient, and
is the combined (averaged over the all internal surfaces) heat transfer
coefficient, and

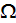 is the volume of heat transfer;
is the volume of heat transfer;
b) pumping power per unit volume

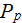

![$[W/m^{3}];$](071-3__34.gif)
c) effectiveness parameter

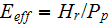 used when the heating flux is unknown
used when the heating flux is unknown
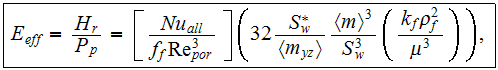 which distinguishes by factor
which distinguishes by factor

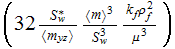 from known ratios of this kind above. The effectiveness number
from known ratios of this kind above. The effectiveness number

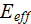 can be explicitly used for comparison of different morphologies. Among
parameters the
can be explicitly used for comparison of different morphologies. Among
parameters the

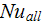 is the Nusselt number when the heat flux from bottom surface is unknown,
is the Nusselt number when the heat flux from bottom surface is unknown,

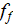 is the Fanning friction factor and
is the Fanning friction factor and

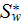

![$\left[ 1/m\right] $](071-3__42.gif) is the overall specific surface in the volume of heat exchange - including
internal
is the overall specific surface in the volume of heat exchange - including
internal

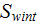 and bottom
and bottom

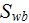 surfaces.
surfaces.
The set of dimensionless numbers which are naturally appear in governing equations of the volume averaging theory (VAT) on the upper scale formulation of heat sink model plus the performance characteristics for heterogeneous medium described above were used directly to control and design the numerical simulation experiments and physical experiments (Travkin et al., 2000).
The bulk (mean) Fanning friction factor

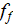 for volume of heat sink was assessed using formulae obtained in SVAT for
experimental measurements of pressure loss (see Travkin and Catton, 1998;
Travkin et al., 1999)
for volume of heat sink was assessed using formulae obtained in SVAT for
experimental measurements of pressure loss (see Travkin and Catton, 1998;
Travkin et al., 1999)
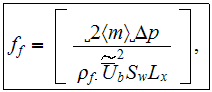 where averaged interstitial bulk velocity
where averaged interstitial bulk velocity

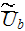 estimated for the whole volume where heat transfer occurs.
estimated for the whole volume where heat transfer occurs.
The three samples studied shown a consistent pattern of declining of friction
factor

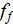 while the porous mediua Reynolds number
while the porous mediua Reynolds number

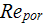 increased. Some wavy like fluctuation of
increased. Some wavy like fluctuation of

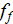 is the usual path monitored thought already in studies over the cross-flow in
tube bundles, see Zhukauskas chapter in Heat Exchangers Design Handbook
(1983). The range of measured Fanning friction factor
is the usual path monitored thought already in studies over the cross-flow in
tube bundles, see Zhukauskas chapter in Heat Exchangers Design Handbook
(1983). The range of measured Fanning friction factor

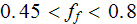 is in the very close vicinity of well known correlations for Fanning friction
factor in this range of Reynolds number defined using the VAT (Travkin and
Catton, 1998).
is in the very close vicinity of well known correlations for Fanning friction
factor in this range of Reynolds number defined using the VAT (Travkin and
Catton, 1998).
Heterogeneous formula for parameter of pumping power per unit volume
using the SVAT was found as
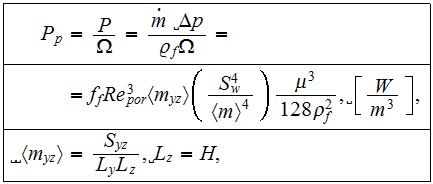 is quite different from usually used homogeneous one (Andrews and Fletcher,
1996)
is quite different from usually used homogeneous one (Andrews and Fletcher,
1996)
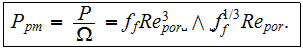 The factor
The factor

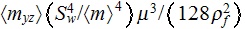 can be associated with the morphological influence
can be associated with the morphological influence

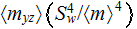 and with the physical characteristics of the cooling fluid
and with the physical characteristics of the cooling fluid

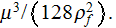
When the heat flux

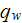 from the bottom is known in the heat exchange device, the heat transfer rate
from the bottom is known in the heat exchange device, the heat transfer rate

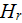 for a known heat flux
for a known heat flux

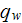 through the bottom surface
through the bottom surface

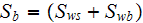 of heterogeneous volumetric device used to be calculated as
of heterogeneous volumetric device used to be calculated as
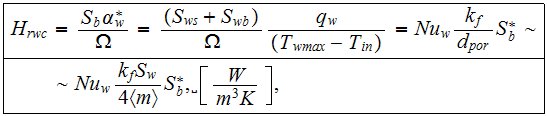
where the value of wall heat transfer coefficient

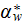

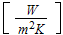 (artificial actually heat transfer coefficient) we do not need to know because
we use the value of assigned (experimental or simulated) bottom wall heat flux
(artificial actually heat transfer coefficient) we do not need to know because
we use the value of assigned (experimental or simulated) bottom wall heat flux

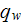

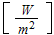 which
is assumed as known. We determine it through the electrical power input. We
recognized in our experimental set-up that the proper defined heat transfer
coefficient
which
is assumed as known. We determine it through the electrical power input. We
recognized in our experimental set-up that the proper defined heat transfer
coefficient

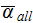 is hardly achievable using current equipment and techniques. At the same time,
we are in the position to know exactly the amount of heat transferring to the
upper base surface and plate fins volume.
is hardly achievable using current equipment and techniques. At the same time,
we are in the position to know exactly the amount of heat transferring to the
upper base surface and plate fins volume.
Then, the effectiveness expression formula

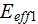 for a heterogeneous volumetric two scale heat transfer device can be written
for a heterogeneous volumetric two scale heat transfer device can be written
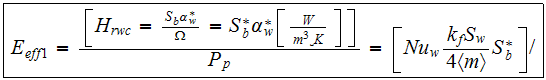
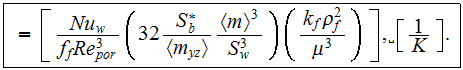 where distinguishing factor
where distinguishing factor

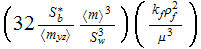 is absent in the known homogeneously developed ratios of this kind as
is absent in the known homogeneously developed ratios of this kind as
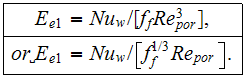
The morphological factor

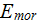 and the physical one
and the physical one

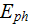 in the definition of
in the definition of

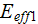 can be expressed as
can be expressed as
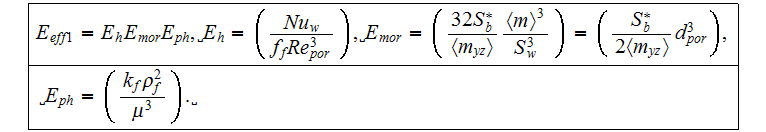
If one to take the effectiveness parameter as

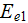 with the established from experiments friction factor
with the established from experiments friction factor

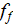 and Reynolds number
and Reynolds number

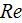 ( which can be even equal to
( which can be even equal to

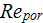 ) data, then there is no visible influence of the morphological factors as it
is in for
) data, then there is no visible influence of the morphological factors as it
is in for

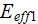 .
.
That means the influence of morphology factors becomes unavailable for
analysis and unknown to researcher. But, implicitly the whole body of research
is actually provided for only to find out these influences more or less
exactly . Numberless studies have been performed with this only goal in mind,
and if these parameters -

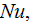

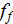 ,
and
,
and

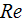 and
particularly
and
particularly

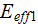 are being determined without care to specify the influence of morphology
openly, explicitly, then there is no choice for obtaining the correct
optimization procedure.
are being determined without care to specify the influence of morphology
openly, explicitly, then there is no choice for obtaining the correct
optimization procedure.
The heat transfer rate

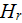 and the effectiveness number
and the effectiveness number

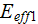 has been explicitly used for comparison of our four sink samples - three
samples with staggered pin fins and one sample with longitudinal fins.
has been explicitly used for comparison of our four sink samples - three
samples with staggered pin fins and one sample with longitudinal fins.
And comparison of those under-VAT experiments with the simplified VAT simulation -
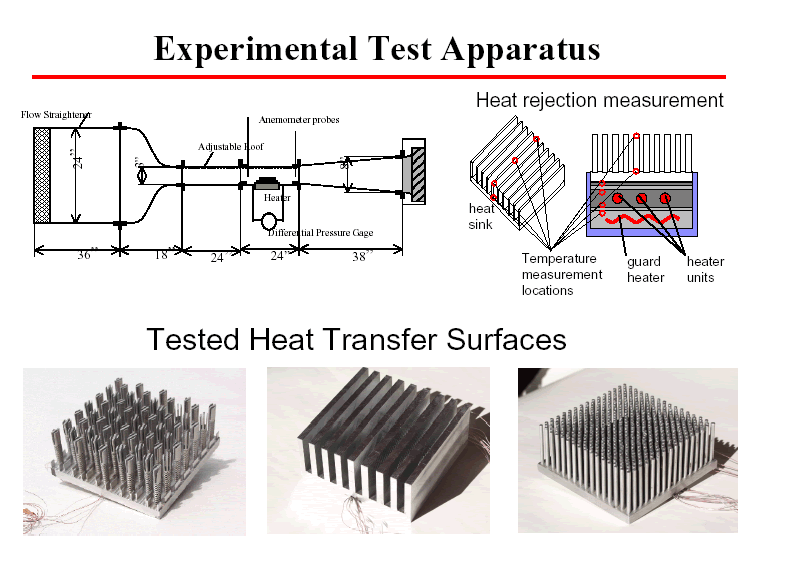
To test the performance of the base to air cooling stage for semiconductor heat removal, an experimental apparatus has been set up. The main part of the experimental apparatus is the wind tunnel. The wind tunnel apparatus was an open loop that propelled air flow through the test section. First, velocity distribution were measured in a test section comprised of a rectangular duct with ribs of square cross section mounted (transverse flow) on the top and bottom channel surfaces. Measurements were taken in a section between two consecutive ribs and from the centerline to the top of the test section - Figure
After testing the validity of the experimental apparatus, the test section was replaced with heat sinks constructed of aluminum and consisted of an array of staggered pin fins.
Each of the heat sinks has constant fin height and constant fin diameter, but the fin pitch is varied. At the bottom of the heat sink, it is a heat generation. Heat generation was accomplished using cartridge heaters insert into a copper block. The generated heat flows upward through a heat meter and to the heat sink. The pressure drop along the heat sink, temperature distribution and total heat dissipated from the heat sink are to be measured. The data is reduced according to the heat sink simplified modeling analysis presented in previous text.
Our Nusselt numbers

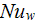 compared with others generally recalculated results using the SVAT formulae
(see Travkin and Catton, 1998; Travkin et al., 1999) showed a substantial
difference for this kind of combined heat transfer in comparison to internal
media heat transfer coefficient correlations.
compared with others generally recalculated results using the SVAT formulae
(see Travkin and Catton, 1998; Travkin et al., 1999) showed a substantial
difference for this kind of combined heat transfer in comparison to internal
media heat transfer coefficient correlations.
See more in following two publications -
2001_semitherm_effectiveness (392K)
Experimental Investigation of Pin Fins (261K)
Then, when first results were analyzed there were some further developments. We got to proceed with the more advanced models to simulate -
We developed the Heterogeneous Separate Phase Based Heat Transfer Parameters for Semiconductor Heat Sinks Experimental Data. The heat transfer process in a semiconductor heat sink embraces processes in both phases - the air and the solid phase. Nevertheless, the only obtained above criteria all belongs and take into account the characteristics of fluid (convective) heat transfer, and not even one coefficient used explicitly which describes the solid phase characteristics.
Near 17-n years ago in the publication by Incropera (1988) there were the words in the p. 1102 we read - "it is common practice to ignore the coupling between heat transfer by conduction in substrate materials and convection to the coolant".
Right now the software packages make the strict enough consideration (simulation) in both parts of the cooler, but - and this is a BIG but - for the lower scale mathematical statement. This means - the overall behavior characteristics, "mean" parameters, averaged characteristics being used (calculated) most often incorrectly, insufficiently. Again, this is because of ignorence of the second - Upper scale models, variables, characteristics.
Reading further in the same p. 1102: "Despite the enormous variability of geometric conditions, systematic attempts have been made to determine component coefficients and to develop methodologies for treating the effect of component location in an array".
But this task is unsolved and up to now! And continue to be unsolved if used the parameters of the upper, more general scale with instruments of the lower scale.
We introduced the heat transfer rate in the solid phase of heat sink. It is
based on the same idea of intensity of heat transfer through the solid phase.
It is assessed as the heat transfer rate (via the solid phase) per unit volume
per unit temperature difference
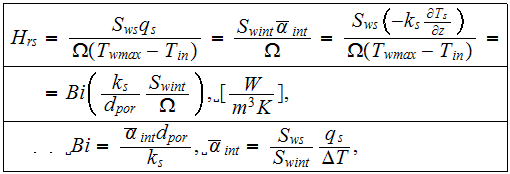 where
where

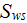 is the bottom solid phase (pin fins or ribs etc.) cross-section area which can
characterize the heat transfer capability of the internal surface of the heat
sink to some extend.
is the bottom solid phase (pin fins or ribs etc.) cross-section area which can
characterize the heat transfer capability of the internal surface of the heat
sink to some extend.
There are the phase based definitions of the effectiveness parameters of solid
phase
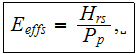 and the bottom flat surface fluid phase heat transfer effectiveness
and the bottom flat surface fluid phase heat transfer effectiveness
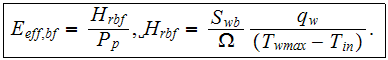
See more two scale simulation features in - INTEGRATED HETEROGENEOUS DESIGN OF SEMICONDUCTOR HEAT SINK VIA SCALED DIRECTED MICRO-MODELING, UPPER SCALE VAT SIMULATION AND EXPERIMENT. COMPARISON VERIFICATION OF PROPERTIES(IMEC2001) (476K)
While further there were involved more hidden attributes into the reality of simulation.
After elaborative study we got to the -
The primary goal for decomposition of the entire set of the SHS performance characteristics was to get more information and understanding of how unequal is in reality the heat exchange in different parts of the SHS . The complete picture and data reduced were obtained from the detailed two phase numerical simulation and will be discussed later. Nevertheless, the physical modeling - experiment is provided to cast a light on the problem by comparing the different modeling approaches.
While considering the problem of experimental set-ups and experimental data reduction for the two-scale semiconductor heat sink, a number of new criteria for momentum and heat transport were derived to connect the local and overall (as temperature in inlet and outlet, etc.) characteristics to the parameters of VAT scaled models. The reason for heterogeneous parameter usage is shown while accomplishing the analysis of the experimental results for heat sink performance -- it yields a better, more exact description of the influence of the media and both phase characteristics on transport values.
These parameters are so specific that they allow one to distinguesh the input of any mechanism or mode of heat transfer occuring in the device. The heat transfer device is presented as two-scale local- non-local heterogeneous heat exchanger with controls on both scales. For example, the heat transfer rates and effectiveness formulated for both phases which improve the energy balance assessment.
We have outlined the consequences of the experimental procedures and design, because the larger number of influencing phenomena make possible the larger number of choices in optimization of performance or in increasing the heat exchange rate to its possible highest level. The latter is the goal of preference in cooling of semiconductor devices.
Experimental results were simulated using the non-local VAT model and also compared to a number of works in the area of heat sink design and simulation:
a) There is the one result which came out of this method and which should be
considered as the one of a good value - is that the separate phase heat
exchange fluxes and parameters are not equal to those averaged over the bottom
surface heat flux and heat transfer rate parameter

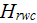 .
.
b) It is worth to note here that in all the simulation procedures pertinent to the phase-separate heat transfer assessments (as well as to one phase SHS performance assessment) there is no need for the heat transfer coeffcient on any surface to be considered or calculated, but for the rudiment resistance assessment.
Another important conclusion is that the heat performance experiment was disclosed from the unusual side allowing to make some assessment about its value.
Above made analysis for the pin fins SHS suggests that the power amount is overcalculated in both submedia - for the pin fins heat transfer rate and for the wetted bottom surface heat transfer rate. But the reasons for that are different:
1) in the case of pin fins - the reason for too big energy amount is - the heat flux in the pins is taken well above the value of it as it is being in reality;
2) in the case of the bottom surface in the pin fins SHS - the reason for the
too large heat dissipated is that - the averaged experimental flux

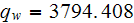 is
also too big - it is averaged over the entire bottom surface including the
relatively higher flux via the pins and unjustifiable and unrealistically high
for the wetted part of the bottom surface.
is
also too big - it is averaged over the entire bottom surface including the
relatively higher flux via the pins and unjustifiable and unrealistically high
for the wetted part of the bottom surface.
That is the one more reason for the better designed experiment - this kind of experiments we did so far are not fit to the standards of the two-scale studies. We will discuss few of the implications in the following sub-sections.
For the ''R'' longitudinal fins SHS:
1) We achieved good heat transfer rates for all three parameters used, for
example, in the data reduction for sink with

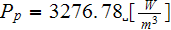 as - the heat transfer rate homogeneous overall
as - the heat transfer rate homogeneous overall

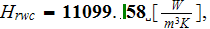 via the bottom surface heat transfer rate
via the bottom surface heat transfer rate

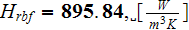 ,
and even via the fins heat transfer rate
,
and even via the fins heat transfer rate

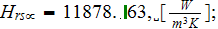
2) We achieved much better energy balance for this SHS: in the fins -

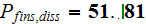

![$\left[ W\right] ;$](071-3__99.gif) at the bottom surface energy balance
at the bottom surface energy balance

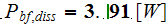 ,
and even the overall device homogeneous energy balance
,
and even the overall device homogeneous energy balance

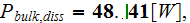 is corresponding to the previous two, when using appropriate values of
temperatures. Summarizing table shows these and other parameters
is corresponding to the previous two, when using appropriate values of
temperatures. Summarizing table shows these and other parameters
  |
  |
 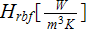 |
 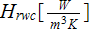 |
 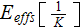 |
|
| Pin fins |  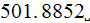 |
 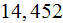 |
 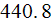 |
 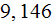 |
 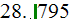 |
| "R" |  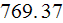 |
 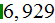 |
 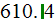 |
 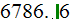 |
 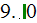 |
| "R" |  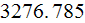 |
 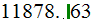 |
 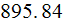 |
 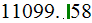 |
 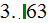 |
 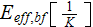 |
 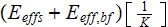 |
 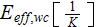 |
 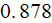 |
  |
  |
 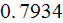 |
 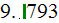 |
 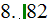 |
 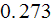 |
 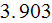 |
 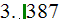 |
There are still the uncertainties in this kind of data collection and reduction for the SHS and we will address these issues in the further studies.
Some of the inconsistencies and inaccuracies in assessments are based or have origins in:
1) The methods of data collection for the temperatures in the fins and on the bottom surface;
2) The magnitudes of particular interest - the heat fluxes are not assessed at the bottom surface and are not connected to the VAT variables.
3) The amount of data measured is not sufficient for the purposes of assessment of surface or fluctuation functions in the subvolumes and over the surfaces.
4) The balances of energies and heat transfer rates are not good enough for the satisfactory grade judgement.
5) The parameters of homogeneous heat transfer assessments - those as the heat
transfer rate

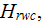 for example, and the effectiveness
for example, and the effectiveness

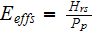 are not related directly and exactly to the VAT upper scale heat transport
statements, and as such have low values in helping to evaluate the process and
to find the better design.
are not related directly and exactly to the VAT upper scale heat transport
statements, and as such have low values in helping to evaluate the process and
to find the better design.
Thus, in the momentum equation those are convective and diffusive heterogeneous fluctuations transport terms in governing equations . In fluid temperature equation, for example, those are the terms with convective fluctuations transport and two terms with surficial effect of inhomogeneous temperature of interface. All of these four terms need to be added to conventional heat flux via interface exchange term (Travkin et al. 2000).
The more complete parameters set for heat exchange rate, pumping power per unit volume and effectiveness were considered in their few forms. We outline the consequences for experimental procedures and design, because the bigger number of influencing phenomena make possible the bigger number of choices in optimization of performance or just in increasing the heat exchange rate. The latter is the goal of preference in cooling of semiconductor devices.
As it was discussed in the previous paragraphs the all matter of formulation of performance parameters or optimization parameters is that it should be related to the formulation of the mathematical model for the process under consideration.
Contrary to the homogeneous medium transport mathematical formulations - the scaled heterogeneous medium mathematical models and governing equations composed in such a way that they contain the additional terms reflecting physical phenomena which are important in heterogeneous medium transport and can not be seen or included in the traditional homogenous formulations. That means, that these additional effects should find their ways to the description or models which reflect the characteristics of performance of the device.
Starting from the analysis of the variables which are the most looked after in
this problem. As one observes that most of variables which usually modeled or
measured are non-local. Below given few of the most pertinent variables and
their actual meanings
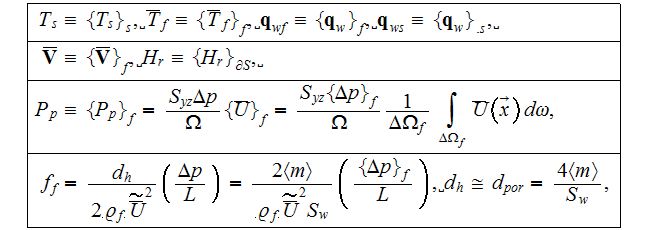 where the phase averaging
where the phase averaging

 and
and

 is
implicitly used, while one needs to recognize that the written notations do
not reflect correctly the conditions of variable's consideration, calculation
or measurement.
is
implicitly used, while one needs to recognize that the written notations do
not reflect correctly the conditions of variable's consideration, calculation
or measurement.
We have used the full written Upper Scale 2D energy
equation for the cooling fluid (air)- because the bottom heat flux starts at a
certain point of flow along of x-axes
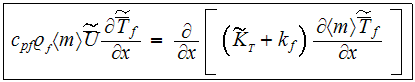
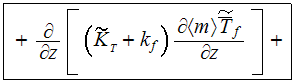
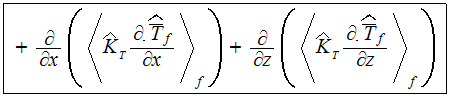
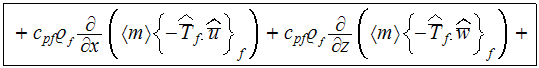
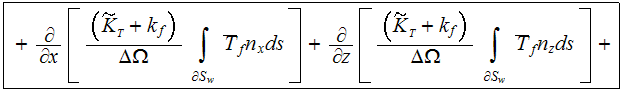
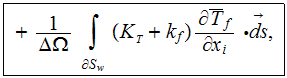 to get the description which is similar by the idea to the formulation of heat
transfer rate
to get the description which is similar by the idea to the formulation of heat
transfer rate

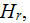 pumping power
pumping power

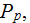 and the effectiveness of the Volumetric Heat Dissipating Device (VHDD).
and the effectiveness of the Volumetric Heat Dissipating Device (VHDD).
Also, the definition of the VA Upper Scale general
heat flux in the fluid can be accepted as for the constant value of porosity

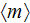 AND THE PERMEABLE INTERFACE in the form -
AND THE PERMEABLE INTERFACE in the form -

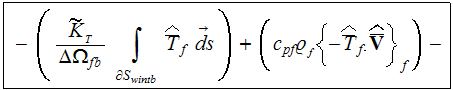
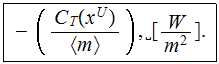 The two-scale DMM-DNM method makes abolished as inaccurate and of low
relevancy some of the developed previously homogeneous
characteristics.
The two-scale DMM-DNM method makes abolished as inaccurate and of low
relevancy some of the developed previously homogeneous
characteristics.


![$[\frac{W}{m^{3}}]$](071-3__152.gif) .
.
To assess the heat transfer rate for the solid phase energy transport the
following expression should be calculated
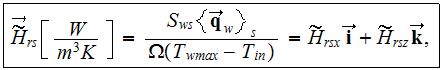 after the full scale - lower (homogeneous) scale level mathematical problem
for the turbulent conjugate transport inside and outside of the "R" SHS was
solved. The vector components of the
after the full scale - lower (homogeneous) scale level mathematical problem
for the turbulent conjugate transport inside and outside of the "R" SHS was
solved. The vector components of the

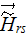 obtained by DMM-DNM are
obtained by DMM-DNM are

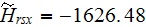

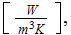

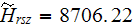

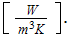 The module of this vector magnitude is the total heat transfer rate via the
solid phase of ''R'' sink
The module of this vector magnitude is the total heat transfer rate via the
solid phase of ''R'' sink
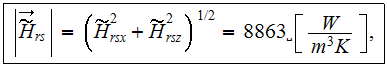
The DMM-DNM simulation of the vector of the heat transfer rate via the solid
phase which is
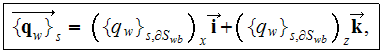 with the overall module of the heat flux as
with the overall module of the heat flux as

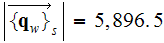

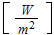 (which is the much less value then the one obtained in experiments
(which is the much less value then the one obtained in experiments

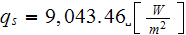 )
)
 From here the amount of energy transferring to the cooling air in the "R" SHS
with the intermediate region characteristics is equal to
From here the amount of energy transferring to the cooling air in the "R" SHS
with the intermediate region characteristics is equal to

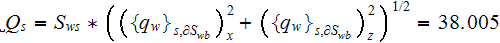

![$\left[ W\right] .$](071-3__166.gif)
The similar kind of modeling for the air side heat transfer rate gave the
components of the heat flux as
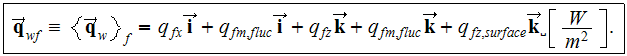
At the same time also the effectiveness of the VAT heat transfer via the fluid
phase is
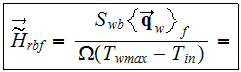
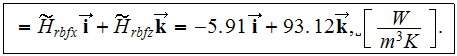
Further, the calculation of the total solid phase diffusion effectiveness gave
the value

While the direct air side bottom effectiveness is
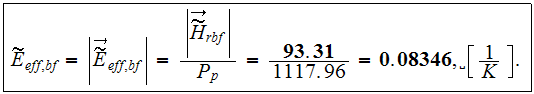
Total effectiveness in this sink was calculated as
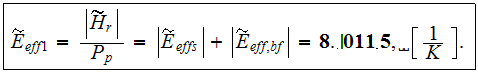
The analysis and conclusions made above comments on the experimentally based heat transfer rates and effectiveness' assessments should be added with the comments on the DMM-DNM results of the two-scale simulation.
1) The obtained parameters of performance are vector functions, not scalar variables common in homogeneous theory of SHS evaluation. This distinction add a lot in understanding of the performance of the heat transfer device as a vector process (directional). These vectorial characteristics increase at least in two times our ability to manipulate the SHS characteristics.
2) Vectorial components of the energy transport in such a simple geometry of SHS as with the longitudinal fins can reach proportions of as much as 20% - that's it the "skeweness" (ratio of smallest component to the module of the vector of the heat effectiveness or other parameters) can be ~20%. In a more complex and inhomogeneous morphology SHS these effects expected to reach much more influence.
3) There are additional physical phenomena which physically known but can not be observed in the modeling through the one-scale homogeneous models. Those are - a) the transport of energy due to fluctuation of fields in the device - "dispersive" transport component; b) the heat transport component due to surficial transport of energy - "interface" transport component.
4) These new components of the bulk heat transport are also the vector components and can be as much as > 10% of the total value of characteristic.
Among the important and unusual results obtained with the two scale VAT formulation of the semiconductor base-to-air stage heat sink mathematical model and its optimization those that concern to and reflect the performance of the device with dependency on morphological parameters, as specific surface, porosity and other geometrical volume specific data.
The scaled VAT formulation allows one to include and highlight phenomena that are not observable when conventional homogeneous modeling is used.
Among these features are the heat transport due to the interface surface (could be a few percent of the overall rate); an exact description of interphase transport and its connection to the morphology (could be 20% or more); field interaction based heat transport (as driven by fluctuations in temperature and in fluid velocity (could be as much as 10%); and nonlinearities resulting from physical models and their coefficients interacting one with another. The VAT based heat sink heat transfer parameters are vector and tensor variables tied directly to the each phase performance.
See some more features in -
We also were able firstly develop some basics for VAT supported (applying the Upper scale SVAT statements) optimization method using so far the readily available simulation approach - statistical Design of Experiment (DOE) methodology
MULTI-VARIANT OPTIMIZATION IN SEMICONDUCTOR HEAT SINK DESIGN (343K)
which was the development of previously stated in OPTIMIZATION OF HEAT TRANSFER EFFECTIVENESS IN HETEROGENEOUS MEDIA (183K) issues.
One of the shorten final reports regarding the results for this problem of semiconductor heat sink can be read in -
Task4-Final-Report-Part-1 (185K)
Task4-Final-Report-Part-2 (404K)
Task4-Final-Report-Part-3 (277K)
After this study performed in cooperation with UCLA and MPEI (Moscow Power Engineering University) (funded by the DOD DARPA in 1998 - 05//2002) and by the later research effort performed in collaboration, also along the proprietary research conditions line we have much wider and clearer picture and knowledge about simulation and experimental methodologies for HSP-VAT based and guided Two Scale VHDD studies.
We have proven the way to connect the heat transfer rate (intensity) characteristics - for conduction as well as for convection, to the governing equations for volumetric heat transfer device (VHTD) or media. There were used the three levels of description for heat and momentum transport processes in these VHTD.
For all three levels of description had been developed the direct connection models communicating the performance of the device to its morphological (which meaning and the heat transfer) characteristics. These connection features are the components of the Upper Scale Mathematical and Physical Models, but not the externally included ratios of geometrical sizes (parameters).
No other theory, method, published or known in the last 15-20 years work can
do these procedures, and other that were discovered in 2000s - up
to now Tuesday, 15-Jul-2025 21:24:12 GMT.
03-/-2013 - Last time new developments, upgrades in other sections of this site conveyed
in the new time brackets,
because this statement above was written in 2003. Since then, we should add at least
11 years - now it is that in the last ~30 years there was created nothing better in
physics for scaled issues
than the old HSP-VAT (Hierarchical Scaled Physics-Volume Averaging Theory),
that was fashioned in the 80s in Europe.
See our latest arguments (among other sections) in -
02//2013 Are Magnet Motors (MM) Exist? Misunderstanding of the Function
02//2013 Failure of Perendev and V-gate MM Homogeneous Designs (Homogeneous Models Do not Exist). Then the Scaled Approach
02//2013 Magnet Motors of M.Yildiz. Major Design Polyscale Features and Solutions. Why These MM Work?
It needs to be stressed out, that the morphology controls for the VHTD performance (characteristics) are the only desirable controls for design when the all other parameters are treated as granted - as when the physical characteristics have been chosen, the external influences (boundary conditions) have been given, etc.
It has been shown (proven) that the heat exchange mechanisms in the two phase (and more) VHTD are different than conventionally excepted in homogeneous one scale physical and mathematical models for these devices, media.
Even generally used in homogeneous statements heat exchange term
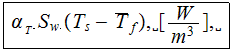 is not equal to any singled out real part of the overall heat transfer process value
between the solid and fluid phases in the heterogeneous volume, neither to the
succeeding from the local flux variable
is not equal to any singled out real part of the overall heat transfer process value
between the solid and fluid phases in the heterogeneous volume, neither to the
succeeding from the local flux variable
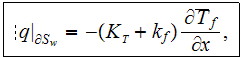
nor to the averaged morpho-exchange term
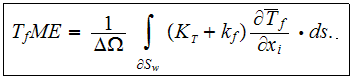
We struggled to deliver this idea in a simplified fashion in the above texts.
As a result of these studies we would repeate here our old statement:
There exists no way to find out, to control or to optimize the performance of the two- or three scale VHTD while using the only Lower Scale modeling equations.
 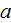 |
- | thermal diffusivity coefficient
 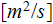 |
 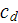 |
- | mean drag resistance coefficient in the REV
 ![$[-]$](071-3__179.gif) |
 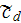 |
- | mean skin friction coefficient over the turbulent area of
 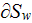
 ![$[-]$](071-3__182.gif) |
 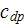 |
- | mean form resistance coefficient in the REV
 ![$[-]$](071-3__184.gif) |
 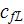 |
- | mean skin friction coefficient over the laminar region inside of the REV
 ![$[-]$](071-3__186.gif) |
 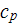 |
- | specific heat
[ 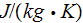 ] ] |
 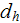 |
- | hydraulic diameter
 ![$[m]$](071-3__190.gif) |
 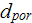 |
- |  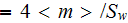 characteristic length
characteristic length
 ![$[m]$](071-3__193.gif) |
 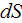 |
- | interphase differential area in porous medium
 ![$[m^{2}]$](071-3__195.gif) |
 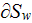 |
- | internal surface in the REV
 ![$[m^{2}]$](071-3__197.gif) |
 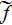 |
- | averaged over
 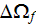 value
value
 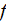 |
 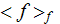 |
- | value
 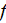 ,
averaged over ,
averaged over
  in a REV
in a REV |
  |
- | value f morpho-fluctuation in a
 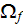 |
 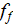 |
- | Fanning friction factor of momentum resistance in the volume [-] |
 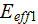 |
- | effectiveness of heat transfer per unit volume
 ![$[1/K]$](071-3__208.gif) |
 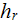 |
- | global heat transfer coefficient of the reference |
flat bottom plate with the same hydraulic resistance
 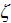 |
||
 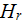 |
- | heat transfer rate per unit volume per unit |
temperature difference
 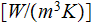 |
 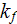 |
- | conductivity coefficient of fluid
phase 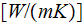 |
 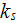 |
- | conductivity coefficient of solid
phase 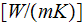 |
 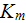 |
- | turbulent eddy viscosity
 ![$[m^{2}/s]$](071-3__218.gif) |
 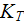 |
- | turbulent eddy thermal conductivity
[ 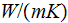 ] ] |
 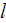 |
- | turbulence mixing length
 ![$[m]$](071-3__222.gif) |
 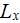 |
- | length of the heat sink (air flow longitudinal x-direction)
 ![$[m]$](071-3__224.gif) |
 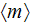 |
- | averaged porosity
 ![$[-]$](071-3__226.gif) |
 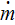 |
- |  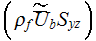 mass flow rate across the channel
mass flow rate across the channel
 ![$[kg/s]$](071-3__229.gif) |
 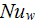 |
- | bottom wall Nusselt number [-] |
 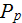 |
- | pumping power per unit of volume
 ![$[W/m^{3}]$](071-3__232.gif) |
 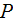 |
- | pumping power
 ![$[W]$](071-3__234.gif) ,
pitch ,
pitch
 ![$[m]$](071-3__235.gif) |
 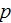 |
- | pressure
 ![$[Pa]$](071-3__237.gif) |
 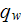 |
- | heat flux through the bottom surface of the heat sink
 ![$[W/m^{2}]$](071-3__239.gif) |
 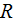 |
- | pore diameter
 ![$[m]$](071-3__241.gif) |
 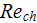 |
- | Reynolds number of pore hydraulic diameter
 ![$[-]$](071-3__243.gif) |
 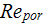 |
- | porous medium Reynolds number
 ![$[-]$](071-3__245.gif) |
 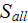 |
- | internal surface plus bottom wall wetted surface
 ![$[m^{2}]$](071-3__247.gif) |
 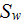 |
- | specific surface of internal volume of SHS |
(bottom surface not included)
 ![$[1/m]$](071-3__249.gif) |
 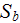 |
- | bottom side full SHS cross-cut
 ![$[m^{2}]$](071-3__251.gif) |
 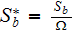 |
bottom side full SHS cross-cut specific surface
 ![$[1/m]$](071-3__253.gif) |
 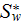 |
- | overall specific surface per unit volume of SHS |
including bottom wetted surface
 ![$[1/m]$](071-3__255.gif) |
||
 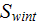 |
- | internal surface
 ![$\ [m^{2}]$](071-3__257.gif) |
 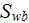 |
- | bottom wetted surface
 ![$[m^{2}]$](071-3__259.gif) |
 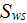 |
- | bottom solid phase cross-cut surface
 ![$[m^{2}]$](071-3__261.gif) |
 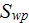 |
- | specific surface of the cross flow projected area of obstacles
 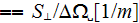 |
 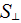 |
- | cross flow projected area of obstacles
[ 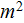 ] ] |
 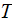 |
- | temperature
 ![$[K]$](071-3__267.gif) |
 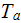 |
- | averaged temperature over vertical coordinate mass flow
 ![$[K]$](071-3__269.gif) |
 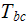 |
- | bulk temperature of the coolant
[ 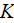 ] ] |
 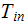 |
- | inlet temperature of the coolant
[ 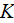 ] ] |
 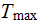 |
- | maximum temperature of the wall
[ 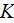 ] ] |
 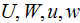 |
- | velocity in x,z-direction
 ![$[m/s]$](071-3__277.gif) |
 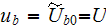 |
- | mean velocity in the fluid for the element of unified medium
 ![$[m/s]$](071-3__279.gif) |
 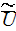 |
- | averaged over the REV interstitial velocity
 ![$[m/s]$](071-3__281.gif) |
 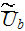 |
- | averaged interstitial (bulk for device, medium) velocity
 ![$[m/s]$](071-3__283.gif) |
 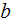 |
- | bulk average |
 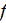 |
- | fluid phase |
 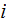 |
- | component of turbulent vector variable |
 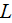 |
- | laminar, lower scale |
 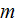 |
- | scale for nondimensionalization |
 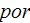 |
- | porous |
 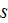 |
- | solid phase |
 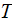 |
- | turbulent |
 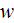 |
- | wall |
 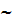 |
- | value in fluid phase averaged over the REV |
 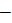 |
- | mean turbulent quantity |
 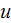 |
- | upper scale |
 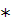 |
- | nondimensional value |
 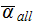 |
- | combined (averaged over the all internal |
and bottom surfaces) heat transfer coefficient
 ![$[W/m^{2}K]$](071-3__298.gif) |
 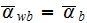 |
- | base wetted surface averaged heat transfer coefficient
 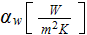 |
 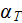 |
- | turbulent heat transfer coefficient
 ![$[W/m^{2}K]$](071-3__302.gif) |
 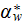 |
- | bottom surface (wetted plus through the solid |
| - | phase-artificial) mean heat transfer coefficient
 ![$[W/m^{2}K]$](071-3__304.gif) |
|
 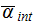 |
- | mean heat transfer coefficient in volume |
of heat sink (averaged over the internal surface)
 ![$[W/m^{2}K]$](071-3__306.gif) |
 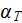 |
- | turbulent heat transfer coefficient
 ![$[W/m^{2}K]$](071-3__308.gif) |
 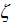 |
- | normalized hydraulic resistance
 ![$[-]$](071-3__310.gif) |
 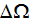 |
- | representative elementary volume (REV)
 ![$[m^{3}]$](071-3__312.gif) |
 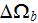 |
- | nearest bottom surface REV containing the fluid phase
 ![$[m^{3}]$](071-3__314.gif) |
 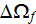 |
- | pore volume in a REV
 ![$[m^{3}]$](071-3__316.gif) |
 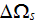 |
- | solid phase volume in a REV
 ![$[m^{3}]$](071-3__318.gif) |
 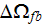 |
- | pore volume in the nearest bottom surface REV
 ![$[m^{3}]$](071-3__320.gif) |
 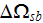 |
- | solid phase volume in the nearest bottom surface REV
 ![$[m^{3}]$](071-3__322.gif) |
 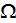 |
- | volume of the heat sink
 ![$[m^{3}]$](071-3__324.gif) |
 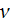 |
- | kinematic viscosity
 ![$[m^{2}/s]$](071-3__326.gif) |
 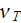 |
- | averaged turbulent eddy viscosity
 ![$[m^{2}/s]$](071-3__328.gif) |
 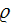 |
- | density
 ![$[kg/m^{3}]$](071-3__330.gif) |
 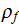 |
- | density of the coolant fluid
 ![$[kg/m^{3}]$](071-3__332.gif) |
 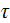 |
- | turbulent friction stress tensor
 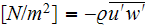 |
 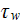 |
- | wall shear stress
 ![$[N/m^{2}]$](071-3__336.gif) |
Achenbach, E., "Heat and Flow Characteristics in Packed Beds," Experimental Thermal and Fluid Science, Vol. 10, pp. 17-21, 1995.
Andrews, M.J. and Fletcher, L.S., "Comparison of Several Heat Transfer Enhancement Technologies for Gas Heat Exchangers," J. Heat Transfer, Vol. 118, pp. 897-902, 1996.
Beavers, G.S. and Sparrow, E.M., "Non-Darcy Flow Through Fibrous Porous Media," J. Applied Mechanics, Vol. 36, pp. 711-714, 1969.
Bejan, A. and Morega, A.M., ''Optimal Arrays of Pin Fins and Plate Fins in Laminar Forced Convection,'' J. Heat Transfer, Vol. 115, pp. 75-81, 1993.
Bejan, A., "The Optimal Spacing for Cylinders in Crossflow Forced Convection," J. Heat Transfer, Vol. 117, pp. 767-770, 1995.
Bejan, A. and Sciubba, E., "The Optimal Spacing of Parallel Plates Cooled by Forced Convection," Int. J. Heat Mass Transfer, Vol. 35, No. 12, pp. 3259-3264, 1992.
Bejan, A., "Constructal Trees of Convective Fins," J. Heat Transfer, Vol. 121, pp. 675-682, 1999.
Ergun, S., "Fluid flow through packed columns," Chemical Engineering Progress, Vol. 48, 89-94, 1952.
Fabbri, G., "Optimum Performances of Longitudinal Convective Fins with Symmetrical and Asymmetrical Profiles", Int. J. Heat Fluid Flow, Vol. 20, pp. 634-641, 1999.
Gortyshov, Yu.F., Muravev, G.B., and Nadyrov, I.N., "Experimental Study of Flow and Heat Exchange in Highly Porous Structures ," Engng.-Phys. Journal, Vol. 53,No. 3, pp. 357-361, (in Russian), 1987.
Gratton, L., Travkin, V.S., and Catton, I., "The Influence of Morphology upon Two- Temperature Statements for Convective Transport in Porous Media," J. Enhanced Heat Transfer, Vol. 3, No. 2, pp.129-145, 1996.
Heat Exchanger Design Handbook, 1983, (Spalding, B.D., Taborek, J., Armstrong, R.C. and et al., contribs.), N.Y., Hemisphere Publishing Corporation, Vol.1,2.
Incropera, F.P., "Convection Heat Transfer in Electronic Cooling", J. Heat Transfer, Vol. 110, pp. 1097-1111, 1988.
Jubran, B.A., Hamdan, M.A., and Abdualh, R.M., " Enhanced Heat Transfer, Missing Pin, and Optimization for Cylindrical Pin Fin Arrays," J. Heat Transfer, Vol. 115, pp. 576-583, 1993.
Kays, W.M. and London, A.L., Compact Heat Exchangers, 3rd ed., McGraw-Hill, New York, 1984.
Kim, S.J. and Kim, D., ''Forced Convection in Microstructures for Electronic Equipment Cooling,'' J. Heat Transfer, Vol. 121, No.3, pp. 639-645, 1999.
Kokorev, V. I., Subbotin, V. I., Fedoseev, V. N., Kharitonov, V.V., and Voskoboinikov, V.V., "Relationship Between Hydraulic Resistance and Heat Transfer in Porous Media," High Temperature, Vol. 25, No. 1, pp. 82-87, 1987.
Macdonald, I.F., El-Sayed, M.S., Mow, K., and Dullien, F.A.L., "Flow through Porous Media - the Ergun Equation Revisited", Ind. Eng. Chem. Fundam., Vol. 18, No. 3, pp. 199-208, 1979.
Rizzi, M., Canino, M., Hu, K., Jones, S., Travkin, V.S., and Catton, I., "Experimental Investigation of Pin Fin Heat Sink Effectiveness," in Proc. NHTC'01, 35th National Heat Transfer Conference, ASME, Anaheim, CA, 2001.
Souto, H.P.A. and Moyne, C., "Dispersion in two dimensional periodic porous media. Part I. Hydrodynamics. Part II. Dispersion Tensor", Phys. Fluids, Vol.9, No.8, p2243-2263, 1997.
Travkin, V.S. and Catton, I., "Models of Turbulent Thermal Diffusivity and Transfer Coefficients for a Regular Packed Bed of Spheres", in Fundamentals of Heat Transfer in Porous Media, ASME HTD-Vol. 193, pp.15-23, 1992.
Travkin, V.S., Gratton, L., and Catton, I., "A Morphological-Approach for Two-Phase Porous Medium-Transport and Optimum Design Applications in Energy Engineering," in Proc. Twelfth Symposium on Energy Engineering Sciences, Argonne National Laboratory, Conf. -9404137, pp. 48-55, 1994.
Travkin, V.S., and Catton, I., "A Two-Temperature Model for Turbulent Flow and Heat Transfer in a Porous Layer", J. Fluids Engineering, Vol. 117, pp. 181-188, 1995.
Travkin, V.S. and Catton, I., Homogeneous and non-local heterogeneous transport phenomena with VAT application analysis, in Proc. 15th Symposium on Energy Engineering Sciences, Argonne National Laboratory, Conf. - 9705121, pp. 48-55, 1997.
Travkin V. S. and Catton, I., ''Porous Media Transport Descriptions - Non-Local, Linear and Nonlinear Against Effective Thermal/Fluid Properties,'' Advances in Colloid and Interface Science, Vol. 76-77, pp. 389-443, 1998.
Travkin, V.S. and I. Catton, ''Compact Heat Exchanger Optimization Tools Based on Volume Averaging Theory,'' in Proc. 33rd ASME NHTC, NHTC99-246, ASME, New Mexico, 1999.
V.S. Travkin, I. Catton, K. Hu, A.T. Ponomarenko, and V.G. Shevchenko, ''Transport Phenomena in Heterogeneous Media: Experimental Data Reduction and Analysis'', in Proc. ASME, AMD-233, Vol. 233, pp. 21-31, 1999.
Travkin, V.S., Catton, I., and Hu, K., ''Optimization of Heat Transfer Effectiveness in Heterogeneous Media,'' in Proc. of the Eighteenth Symposium on Energy Engineering Sciences, Argonne National Laboratory, 2000.
Travkin, V.S., Hu, K., and Catton, I., "Multi-variant Optimization in Semiconductor Heat Sink Design," in Proc. NHTC'01, 35th National Heat Transfer Conference, ASME, Anaheim, CA, 2001a.
Travkin, V.S., Hu, K., Rizzi, M., Canino, M., and Catton, I., (2001), "Revising the Goals and Means for the Base-to-Air Cooling Stage for Semiconductor Heat Removal - Experiments and Their Results," in Proc. 17th IEEE SEMI-THERM Symp., pp. 85-94, 2001b.
Vafai, K. and Tien, C.L., "Boundary and Inertia Effects on Flow and Heat Transfer in Porous Media," Int. J. Heat and Mass Transfer, Vol. 24, pp. 195-203, 1981.
You, H.-I.,and Chang, C.-H., "Numerical Prediction of Heat Transfer Coefficient for a Pin-Fin Channel FLow", J. Heat Tansfer, Vol. 119, No. 4, pp. 840-843, 1997.

![]()